高中数学必修5：8_示范教案（1_3　实习作业）

高中数学必修5：8_示范教案（1_3　实习作业）

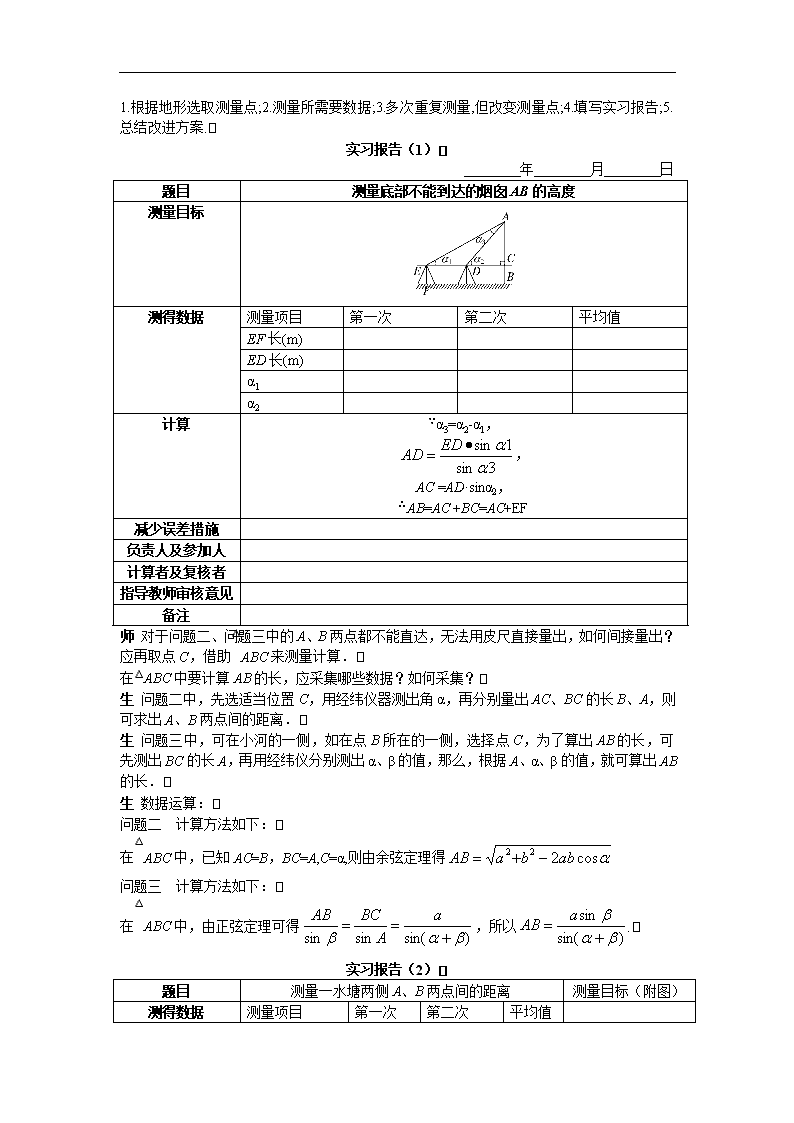
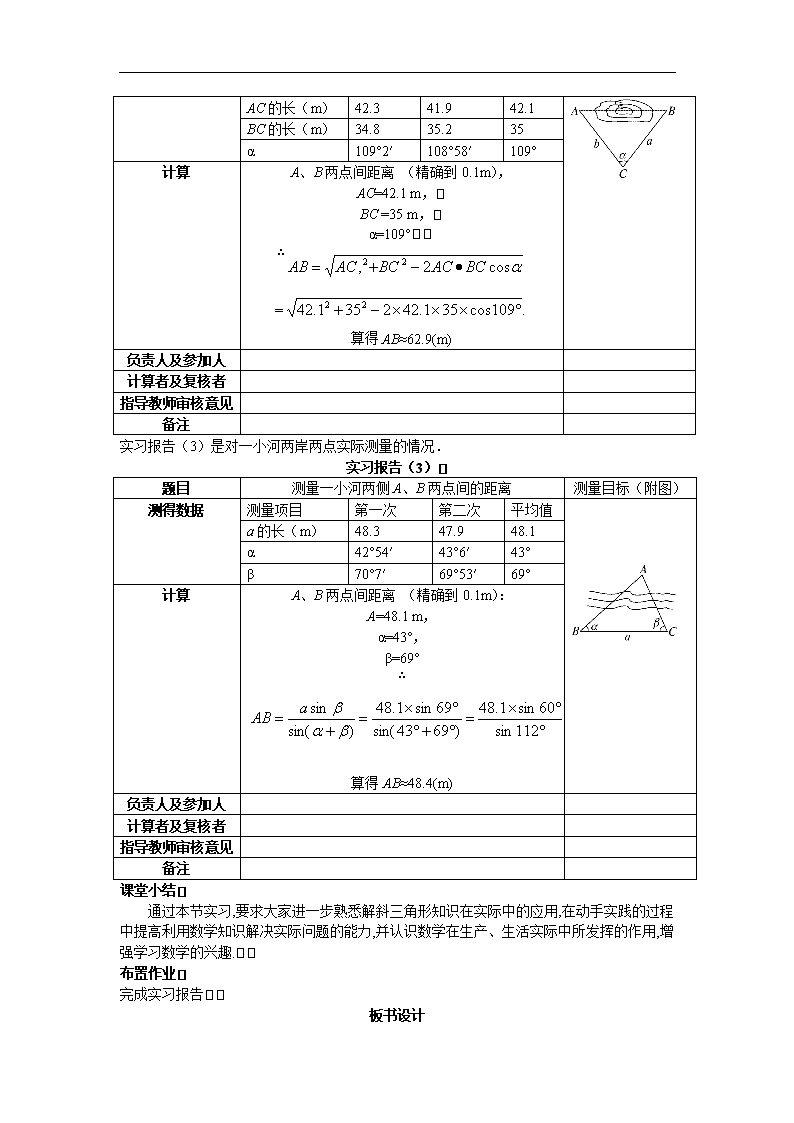
‎1.3　实习作业 从容说课 本节适当安排了一些实习作业，目的是让学生进一步巩固所学的知识，提高学生分析问题解决问题的能力、动手操作的能力以及用数学语言表达实习过程和实习结果的能力，增强学生应用数学的意识和数学实践的能力．教师要注意对于学生实习作业的指导，包括对于实际测量问题的选择，及时纠正实际操作中的错误，解决测量中出现的一些问题． 教学重点 数学模型的建立. 教学难点 解斜三角形知识在实际中的应用. 教具准备 测量工具（三角板、测角仪、米尺等）、实习报告 三维目标 一、知识与技能 ‎1.解斜三角形应用; ‎2.测角仪原理; ‎3.数学建模. 二、过程与方法 ‎1.进一步熟悉解斜三角形知识; ‎2.巩固所学知识,提高分析和解决简单实际问题的能力; ‎3.加强动手操作的能力; ‎4.进一步提高数学语言表达实习过程和实习结果的能力;  ‎5.增强数学应用意识. 三、情感态度与价值观 ‎1.认识数学在生产实际中的作用; ‎2.提高学习数学兴趣,树立建设祖国的远大理想. 导入新课 师 前面几节课，我们一起学习了解斜三角形的应用举例,具备了一定的解斜三角形的能力,并且了解到解斜三角形知识在生产、生活实际的各个方面的应用. 这一节,我们将一起动手应用解斜三角形的知识来研究实际问题.‎ 推进新课 ‎（1）提出问题：问题（一）：测量学校锅炉房的烟囱的高度. 问题（二）：如图(1)，怎样测量一水塘两侧A、B两点间的距离? 问题（三）：如图(2)，若要测量小河两岸A、B两点间的距离，应怎样测量？ ‎(1)‎ ‎(2) ‎（2）分析问题： 师 问题（一）中的学校锅炉房的烟囱的高度无法用皮尺直接量出，那应该怎么去解决？ 生 根据实际情况，应该采取下列措施： ‎1.根据地形选取测量点;2.测量所需要数据;3.多次重复测量,但改变测量点;4.填写实习报告;5.总结改进方案. 实习报告（1） ‎　　　　年　　　　月　　　　日 题目 测量底部不能到达的烟囱AB的高度 测量目标 测得数据 测量项目 第一次 第二次 平均值 EF长(m)‎ ED长(m)‎ α1‎ α2‎ 计算 ‎∵α3=α2-α1，‎ ‎，‎ AC =AD·sinα2， ‎ ‎∴AB=AC +BC=AC+EF 减少误差措施 负责人及参加人 计算者及复核者 指导教师审核意见 备注 师 对于问题二、问题三中的A、B两点都不能直达，无法用皮尺直接量出，如何间接量出？应再取点C，借助△ABC来测量计算． 在△ABC中要计算AB的长，应采集哪些数据？如何采集？ 生 问题二中，先选适当位置C，用经纬仪器测出角α，再分别量出AC、BC的长B、A，则可求出A、B两点间的距离． 生 问题三中，可在小河的一侧，如在点B所在的一侧，选择点C，为了算出AB的长，可先测出BC的长A，再用经纬仪分别测出α、β的值，那么，根据A、α、β的值，就可算出AB的长． 生 数据运算： 问题二　计算方法如下： 在△ABC中，已知AC=B，BC=A,C=α,则由余弦定理得 问题三　计算方法如下： 在△ABC中，由正弦定理可得，所以. 实习报告（2） 题目 测量一水塘两侧A、B两点间的距离 测量目标（附图）‎ 测得数据 测量项目 第一次 第二次 平均值 AC的长（m）‎ ‎42.3‎ ‎41.9‎ ‎42.1‎ BC的长（m）‎ ‎34.8‎ ‎35.2‎ ‎35‎ α ‎109°2′‎ ‎108°58′‎ ‎109°‎ 计算 A、B两点间距离 （精确到0.1m），‎ AC=42.1 m， BC =35 m， α=109° ‎∴‎ ‎=‎ 算得AB≈62.9(m)‎ 负责人及参加人 计算者及复核者 指导教师审核意见 备注 实习报告（3）是对一小河两岸两点实际测量的情况．‎ 实习报告（3） 题目 测量一小河两侧A、B两点间的距离 测量目标（附图）‎ 测得数据 测量项目 第一次 第二次 平均值 a的长（m）‎ ‎48.3‎ ‎47.9‎ ‎48.1‎ α ‎42°54′‎ ‎43°6′‎ ‎43°‎ β ‎70°7′‎ ‎69°53′‎ ‎69°‎ 计算 A、B两点间距离 （精确到0.1m）：‎ A=48.1 m，‎ α=43°，‎ β=69°‎ ‎∴‎ 算得AB≈48.4(m)‎ 负责人及参加人 计算者及复核者 指导教师审核意见 备注 课堂小结 通过本节实习,要求大家进一步熟悉解斜三角形知识在实际中的应用,在动手实践的过程中提高利用数学知识解决实际问题的能力,并认识数学在生产、生活实际中所发挥的作用,增强学习数学的兴趣. 布置作业 完成实习报告 板书设计 实习作业 提出问题 分析问题 实习报告 ‎　　　　　　　　　　　　　　　 课堂小结 布置作业