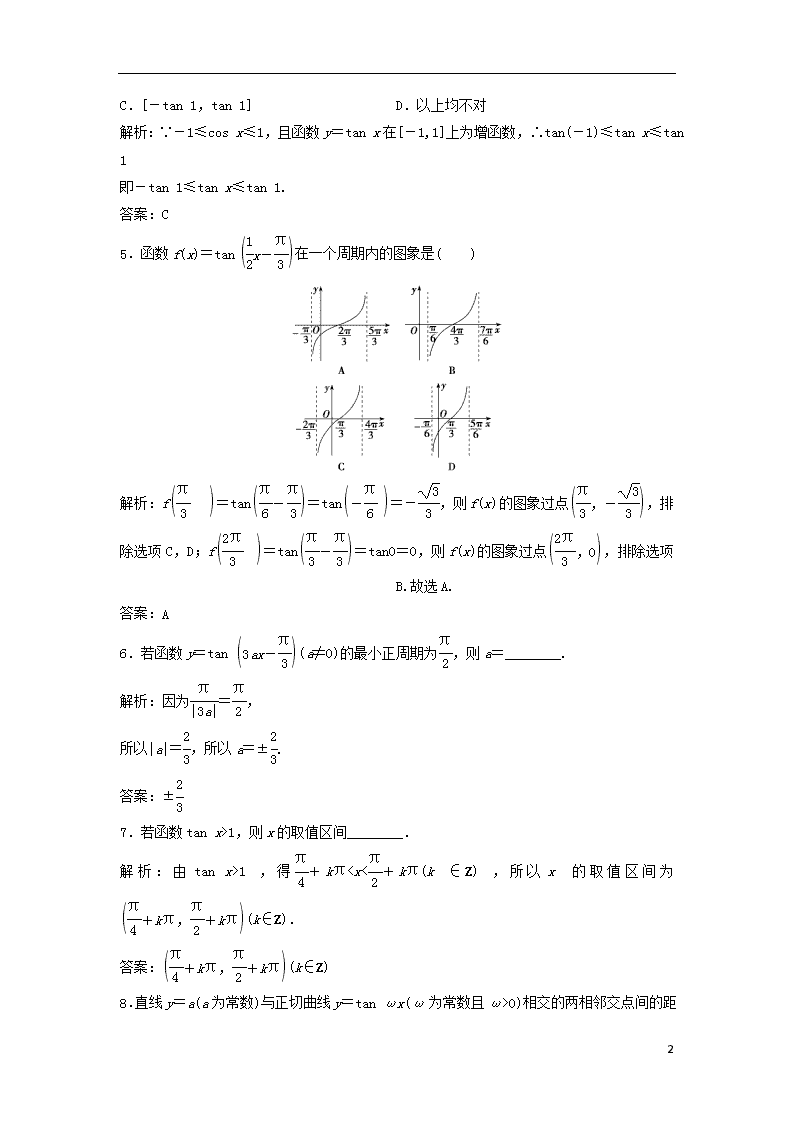2020年高中数学第一章三角函数1
1.4.3 正切函数的性质与图象
[课时作业]
[A组 基础巩固]
1.函数y=tan 的定义域是( )
A.
B.
C.
D.
解析:y=tan =-tan ,
所以x-≠kπ+,k∈Z,
所以x≠kπ+,k∈Z,x∈R.
答案:D
2.下列说法正确的是( )
A.y=tan x是增函数
B.y=tan x在第一象限是增函数
C.y=tan x在每个区间(k∈Z)上是增函数
D.y=tan x在某一区间上是减函数
解析:正切函数在每个区间(k∈Z)上是增函数.但在整个定义域上不是增函数,另外,正切函数不存在减区间.
答案:C
3.已知a=tan 2,b=tan 3,c=tan 5,不通过求值,判断下列大小关系正确的是( )
A.a>b>c B.a
a>c D.btan 2>tan(5-π).
答案:C
4.函数y=tan(cos x)的值域是( )
A.[-,] B.[-,]
5
C.[-tan 1,tan 1] D.以上均不对
解析:∵-1≤cos x≤1,且函数y=tan x在[-1,1]上为增函数,∴tan(-1)≤tan x≤tan 1
即-tan 1≤tan x≤tan 1.
答案:C
5.函数f(x)=tan在一个周期内的图象是( )
解析:f=tan=tan=-,则f(x)的图象过点,排除选项C,D;f=tan=tan0=0,则f(x)的图象过点,排除选项 B.故选A.
答案:A
6.若函数y=tan (a≠0)的最小正周期为,则a=________.
解析:因为=,
所以|a|=,所以a=±.
答案:±
7.若函数tan x>1,则x的取值区间________.
解析:由tan x>1,得+kπ0)相交的两相邻交点间的距离为________.
5
解析:∵ω>0,∴函数y=tan ωx的周期为.
且在每一个独立的区间内都是单调函数,∴两交点间的距离为.
答案:
9.求函数y=tan 的单调增区间.
解析:由kπ-<2x+0)的图象的相邻两支截直线y=所得线段长为,则f()=________.
解析:∵ω>0,∴函数f(x)=tan ωx的周期为,且在每个独立区间内都是单调函数,
5
∴两交点之间的距离为=,∴ω=4,f(x)=
tan 4x,∴f()=tan π=0.
答案:0
5.已知x∈,求函数y=+2tan x+1的最值及相应的x的值.
解析:y=+2tan x+1=+2tan x+1
=tan2x+2tan x+2=(tan x+1)2+1.
∵x∈,∴tan x∈[-,1].
当tan x=-1,即x=-时,y取得最小值1;
当tan x=1,即x=时,y取得最大值5.
6.已知f(x)=x2+2x·tan θ-1,x∈[-1, ],其中θ∈.
(1)当θ=-时,求函数f(x)的最大值与最小值;
(2)求θ的取值范围,且使y=f(x)在区间[-1, ]上是单调函数.
解析:(1)当θ=-时,f (x)=x2-x-1=2-,x∈[-1,],
所以当x=时,f(x)的最小值为-,
当x=-1时,f(x)的最大值为.
(2)因为f(x)=x2+2x·tan θ-1=(x+tan θ)2-1-tan2θ,
所以原函数的图象的对称轴方程为x=-tan θ.
因为y=f(x)在[-1,]上是单调函数,
所以-tan θ≤-1或-tan θ≥,
即tan θ≥1或tan θ≤-,
所以+kπ≤θ<+kπ或-+kπ<θ≤-+kπ,k∈Z.
又θ∈,
所以θ的取值范围是∪.
5