辽宁省联合校2020-2021学年高二上学期第一次月考数学试题 Word版含答案

辽宁省联合校2020-2021学年高二上学期第一次月考数学试题 Word版含答案

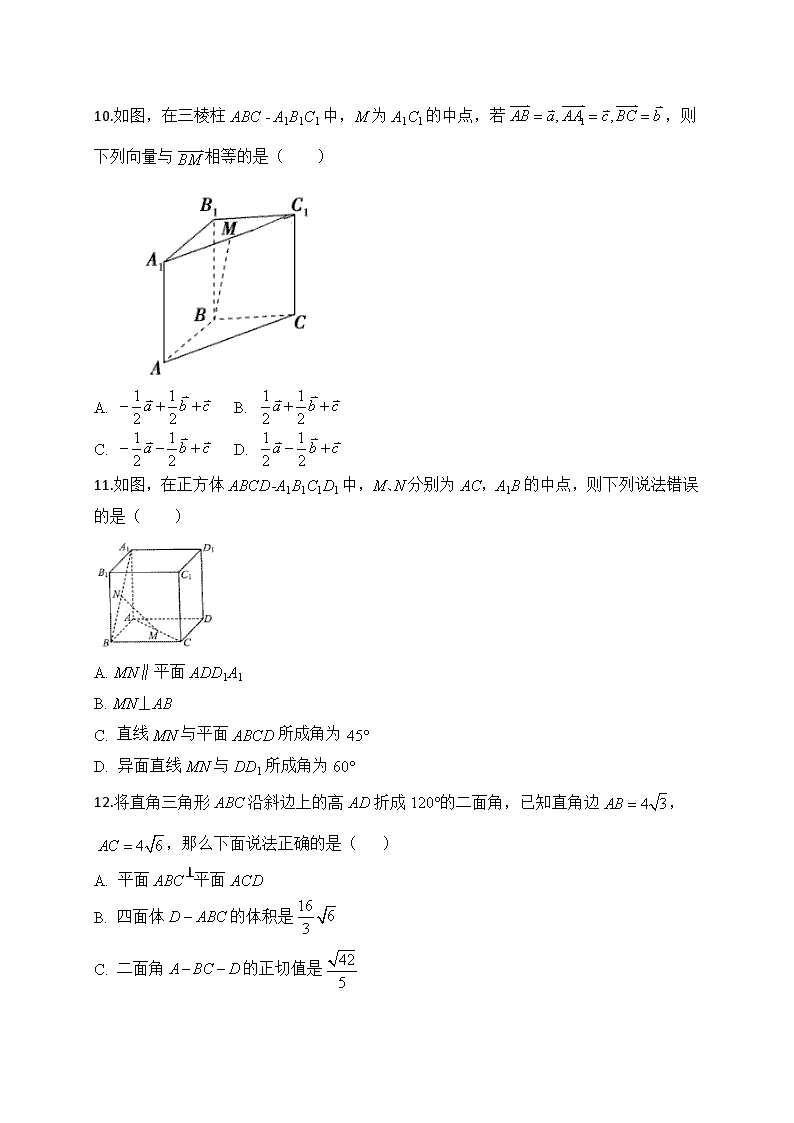
绝密★启用前 联合校第一次考试 高二数学 命题人：凌海三高数学组 考试时间：120分钟 试卷满分：150分 学校:___________姓名：___________班级：___________考号：___________‎ 一、选择题（每题5分，满分60分）‎ ‎1.已知向量，，则（ ）‎ A. (－1,1,5) B. (－3,5,－3) ‎ C. (3,－5,3) D. (1,－1,－5) ‎ ‎2.点到原点的距离为（　　）‎ A. 1 B. 3 C. 5 D. 9‎ ‎3.已如向量，且与互相垂直，则k= ‎ A. B. C. D. ‎ ‎4.若向量，且与的夹角余弦为，则等于（ ）‎ A. B. C. 或 D. 2‎ ‎5.如图，长方体ABCD - A1B1C1D1中，，，那么异面直线与所成角的余弦值是（ ）‎ A. B. C. D. ‎ ‎6.已知正四棱柱ABCD - A1B1C1D1，设直线AB1与平面所成的角为，直线CD1‎ 与直线A1C1所成的角为，则（ ）‎ A. B. C. D. ‎ ‎7.如图，已知空间四边形OABC，其对角线为OB、AC，M、N分别是对边OB、AC的中点，点G在线段MN上，，现用基向量表示向量，设，则的值分别是（ ）‎ A. B. ‎ C. D. ‎ ‎8.如图，60°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB．已知，则CD的长为 ‎ ‎ A. B. 7 C. D. 9‎ ‎9.在正方体ABCD﹣A1B1C1D1中，E是BB1的中点，若，则点B到平面ACE的距离等于（ ）‎ A. B. C. D. 3‎ ‎10.如图，在三棱柱ABC - A1B1C1中，M为A1C1的中点，若，则下列向量与相等的是（　　）‎ A. B. ‎ C. D. ‎ ‎11.如图，在正方体ABCD-A1B1C1D1中，M､N分别为AC，A1B的中点，则下列说法错误的是（ ）‎ A. MN∥平面ADD1A1‎ B. MN⊥AB C. 直线MN与平面ABCD所成角为45°‎ D. 异面直线MN与DD1所成角为60°‎ ‎12.将直角三角形ABC沿斜边上的高AD折成120°的二面角，已知直角边，，那么下面说法正确的是（ ）‎ A. 平面ABC⊥平面ACD B. 四面体的体积是 C. 二面角的正切值是 D. BC与平面ACD所成角的正弦值是 二、填空题（每题5分，满分20分）‎ ‎13.若平面的一个法向量为，直线l的一个方向向量为，则l与所成角的正弦值为________.‎ ‎14.若同方向的单位向量是________________‎ ‎15.在空间直角坐标系O-xyz中，设点M是点关于坐标平面xOy的对称点，点关于x轴对称点Q，则线段MQ的长度等于__________．‎ ‎16.已知平行六面体ABCD﹣A1B1C1D1所有棱长均为1，∠BAD=∠BAA1=∠DAA1=60°，则AC1的长为　　．‎ 三解答题（共6个解答题，17题10分，其余每题12分）‎ ‎17.如图，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．‎ ‎(1)求异面直线BE与AC所成角的余弦值；‎ ‎(2)求直线BE和平面ABC的所成角的正弦值．‎ ‎18.如图.在四棱锥P-ABCD中，平面ABCD，且，，，，，.‎ ‎（1）求异面直线PC与AD所成角的余弦 ‎（2）求点A到平面PCD的距离.‎ ‎19.如图，已知三棱锥的侧棱两两垂直，且，，是的中点。‎ ‎（1）求异面直线与所成角的余弦值；‎ ‎（2）求点E到面ABC的距离。‎ ‎（3）求二面角的平面角的正切值。‎ ‎20.如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，，，，D，E分别为线段AB，BC上的点，且，，.‎ (1) 求证：PD⊥平面ABC；‎ ‎(2)若直线PA与平面ABC所成的角为，求平面PAC与平面PDE所成的锐二面角．‎ ‎21.如图，四棱锥P-ABCD的底面ABCD为平行四边形，PA⊥底面ABCD，，，，.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）若E是侧棱PC上的一点，且BE与底面ABCD所成的是为45°，求二面角的余弦值.‎ ‎22如图四边形PABC中，，，现把沿AC折起，使PA与平面ABC成，设此时P在平面ABC上的投影为O点（O与B在AC的同侧），‎ ‎（1）求证：OB∥平面PAC；‎ ‎（2）求二面角P－BC－A大小的正切值。‎ ‎ ‎ 联合校第一次考试答案 一：选择 A,C,B,A,A DDCBA DD ‎ 二：填空 ‎；；；‎ 三：解答 ‎17：解析：（1）以O为原点，OB、OC、OA分别为X、Y、Z轴建立空间直角坐标系．‎ 则有A（0，0，1）、B（2，0，0）、C（0，2，0）、E（0，1，0）…‎ ‎∴，‎ ‎∴COS＜＞==﹣ ‎ 所以异面直线BE与AC所成角的余弦为…‎ ‎（2）设平面ABC的法向量为则 知 知取，…‎ 则…‎ 故BE和平面ABC的所成角的正弦值为 ‎18【详解】（1）以为原点，为轴，为轴，为轴，建立如图所示空间直角坐标系，‎ 则，，，‎ ‎，，‎ 设异面直线与所成角为，‎ 则，‎ ‎（2）设平面的一个法向量为，，，‎ ‎，，‎ 则，取，得，‎ ‎∴点到平面的距离.‎ ‎19.‎ 又，‎ ‎ ‎ ‎（3）（2）中已求平面ABC的法向量，设平面EAB的法向量为 ‎ ‎ 取。 。 ‎ 设二面角的平面角为，则。‎ ‎20：【详解】(1)由题意知，，，‎ 所以，‎ 所以，所以，‎ 又易知，‎ 所以，‎ 所以，又，‎ 所以，‎ 所以，‎ 因为平面平面，交线为，‎ 所以平面，所以，‎ 因为，，‎ 所以平面；‎ ‎(2)由(1)知，，两两互相垂直，所以可建立如图所示的直角坐标系，‎ 因为直线与平面所成的角为，即，所以，‎ 则，，，，‎ 所以，，．‎ 因为，，所以，‎ 由(1)知，所以，‎ 又平面，所以，‎ 因为，‎ 所以平面，‎ 所以为平面的一个法向量．‎ 设平面的法向量为，则，‎ 所以，令，得，，‎ 所以为平面的一个法向量．‎ 所以，‎ 所以平面与平面所成的锐二面角的余弦值为，‎ 故平面与平面所成的锐二面角为.:‎ ‎21：【详解】（Ⅰ）在平行四边形中，，，，‎ 由余弦定理得，‎ 可得，所以，即，‎ 又底面，底面，所以，‎ 又 所以平面，‎ 又平面，所以平面平面.‎ ‎（Ⅱ）如图所示，以A为坐标原点，，，所在直线分别为x轴，y轴，z 轴，建立空间直角坐标系，‎ 则，，，，，‎ 设，，‎ 因为，，‎ 又因为，所以，‎ 又由平面的一个法向量为，‎ 所以，‎ 解得，即，‎ 设平面的法向量为，平面的法向量为，‎ 由，，‎ 因为，，可得，取，得，‎ 同理可得 ，‎ 由，‎ 因为二面角为钝角，所以二面角的余弦值为.‎ ‎22.解：（1）连AO，因为平面ABC，得。‎ 又因为，得平面PAO，。‎ 因为是PA与平面ABC的角，。‎ 因为，得。‎ 在中，，故有，‎ 从而有，得平面PAC。 ‎ ‎（2）过O作BC的垂线交CB延长线于G点，连PG，则是二面角P－BC－A的平面角。‎ 在中，易知，‎ 所以 另解：（1）同上 ‎（2）以OB、OA、OP为x、y、z轴，建立坐标系，可得。‎ 可求得平面ABC的法向量是，平面PBC的法向量是，所以二面角P－BC－A大小的余弦值是，即 ‎