2021届高考数学一轮复习第三章导数及其应用第2节第1课时导数与函数的单调性课件新人教A版

2021届高考数学一轮复习第三章导数及其应用第2节第1课时导数与函数的单调性课件新人教A版

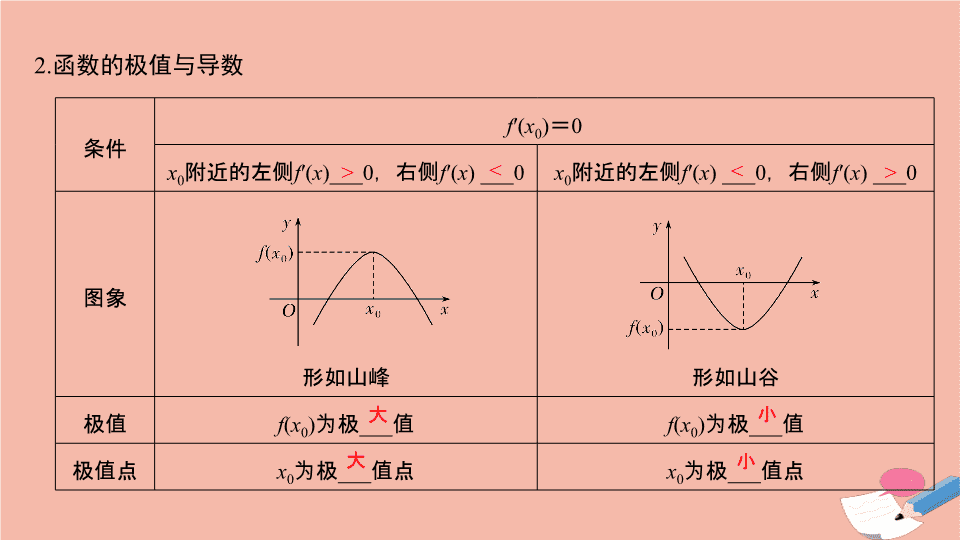
第 2 节　导数在研究函数中的应用 考试要求　 1. 了解函数的单调性与导数的关系；能利用导数研究函数的单调性，会求函数的单调区间 ( 其中多项式函数不超过三次 ) ； 2. 了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值 ( 其中多项式函数不超过三次 ) ；会求闭区间上函数的最大值、最小值 ( 其中多项式函数不超过三次 ) ； 3. 利用导数研究函数的单调性、极 ( 最 ) 值，并会解决与之有关的方程 ( 不等式 ) 问题； 4. 会利用导数解决某些简单的实际问题 . 知 识 梳 理 单调递增 1. 函数的单调性与导数的关系 函数 y ＝ f ( x ) 在某个区间内可导，则： (1) 若 f ′( x )>0 ，则 f ( x ) 在这个区间内 ____________ ； (2) 若 f ′( x )<0 ，则 f ( x ) 在这个区间内 ____________ ； (3) 若 f ′( x ) ＝ 0 ，则 f ( x ) 在这个区间内是 ____________ . 单调递减 常数函数 2. 函数的极值与导数 条件 f ′( x 0 ) ＝ 0 x 0 附近的左侧 f ′( x )___0 ，右侧 f ′( x ) ___0 x 0 附近的左侧 f ′( x ) ___0 ，右侧 f ′( x ) ___0 图象 形如山峰 形如山谷 极值 f ( x 0 ) 为极 ___ 值 f ( x 0 ) 为极 ___ 值 极值点 x 0 为极 ___ 值点 x 0 为极 ___ 值点 > < < > 大 小 大 小 3. 函数的最值与导数 (1) 函数 f ( x ) 在 [ a ， b ] 上有最值的条件 如果在区间 [ a ， b ] 上函数 y ＝ f ( x ) 的图象是一条 ____________ 的曲线，那么它必有最大值和最小值 . (2) 求 y ＝ f ( x ) 在 [ a ， b ] 上的最大 ( 小 ) 值的步骤 ① 求函数 y ＝ f ( x ) 在 ( a ， b ) 内的 _______ ； ② 将函数 y ＝ f ( x ) 的各极值与端点处的函数值 f ( a ) ， f ( b ) 比较，其中 _______ 的一个是最大值， _______ 的一个是最小值 . 连续不断 极值 最大 最小 [ 常用结论与微点提醒 ] 1. 若函数 f ( x ) 在区间 ( a ， b ) 上递增，则 f ′( x ) ≥ 0 ，所以 “ f ′( x )>0 在 ( a ， b ) 上成立 ” 是 “ f ( x ) 在 ( a ， b ) 上单调递增 ” 的充分不必要条件 . 2. 对于可导函数 f ( x ) ， “ f ′( x 0 ) ＝ 0 ” 是 “ 函数 f ( x ) 在 x ＝ x 0 处有极值 ” 的必要不充分条件 . 3. 求最值时，应注意极值点与所给区间的关系，关系不确定时，需要分类讨论，不可想当然认为极值就是最值 . 4. 函数最值是 “ 整体 ” 概念，而函数极值是 “ 局部 ” 概念，极大值与极小值之间没有必然的大小关系 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1) 若函数 f ( x ) 在 ( a ， b ) 内单调递增，那么一定有 f ′( x )>0.( 　　 ) (2) 如果函数 f ( x ) 在某个区间内恒有 f ′( x ) ＝ 0 ，则 f ( x ) 在此区间内没有单调性 .( 　　 ) (3) 函数的极大值一定大于其极小值 .( 　　 ) (4) 对可导函数 f ( x ) ，若 f ′( x 0 ) ＝ 0 ，则 x 0 为极值点 .( 　　 ) (5) 函数的最大值不一定是极大值，函数的最小值也不一定是极小值 .( 　　 ) 解析　 (1) f ( x ) 在 ( a ， b ) 内单调递增，则有 f ′( x ) ≥ 0. (3) 函数的极大值也可能小于极小值 . (4) x 0 为 f ( x ) 的极值点的充要条件是 f ′( x 0 ) ＝ 0 ，且 x 0 两侧导函数异号 . 答案 　 (1) × 　 (2) √ 　 (3) × 　 (4) × 　 (5) √ 2. ( 老教材选修 2 － 2P32A4 改编 ) 如图是 f ( x ) 的导函数 f ′( x ) 的图象，则 f ( x ) 的极小值点的个数为 ( 　　 ) A.1 B.2 C.3 D.4 解析　 由题意知在 x ＝－ 1 处 f ′( － 1) ＝ 0 ，且其两侧导数符号为左负右正 . 答案　 A 3. ( 老教材选修 2 － 2P26 练习 T1 改编 ) 函数 f ( x ) ＝ x 2 － 2ln x 的单调递减区间是 ( 　　 ) A.(0 ， 1] B.[1 ，＋ ∞ ) C.( － ∞ ，－ 1] D.[ － 1 ， 0) ∪ (0 ， 1] 4. (2017· 浙江卷 ) 函数 y ＝ f ( x ) 的导函数 y ＝ f ′( x ) 的图象如图所示，则函数 y ＝ f ( x ) 的图象可能是 ( 　　 ) 解析　 设导函数 y ＝ f ′( x ) 与 x 轴交点的横坐标从左往右依次为 x 1 ， x 2 ， x 3 ，由导函数 y ＝ f ′( x ) 的图象易得当 x ∈ ( － ∞ ， x 1 ) ∪ ( x 2 ， x 3 ) 时， f ′( x )<0 ；当 x ∈ ( x 1 ， x 2 ) ∪ ( x 3 ，＋ ∞ ) 时， f ′( x )>0( 其中 x 1 <0< x 2 < x 3 ) ，所以函数 f ( x ) 在 ( － ∞ ， x 1 ) ， ( x 2 ， x 3 ) 上单调递减，在 ( x 1 ， x 2 ) ， ( x 3 ，＋ ∞ ) 上单调递增，观察各选项，只有 D 选项符合 . 答案 　 D A.(1 ， 2] B.[4 ，＋ ∞ ) C.( － ∞ ， 2] D.(0 ， 3] 解析　 f ′( x ) ＝ x 2 － 4 ， x ∈ [0 ， 3] ，当 x ∈ [0 ， 2) 时， f ′( x )<0 ，当 x ∈ (2 ， 3] 时， f ′( x )>0 ，所以 f ( x ) 在 [0 ， 2) 上是减函数，在 (2 ， 3] 上是增函数 . 又 f (0) ＝ m ， f (3) ＝－ 3 ＋ m . 所以在 [0 ， 3] 上， f ( x ) max ＝ f (0) ＝ 4 ，所以 m ＝ 4. 答案　 4 第一课时　导数与函数的单调性 (1) 讨论 f ( x ) 的单调性； (2) 若 f ( x ) ≥ 0 ，求 a 的取值范围 . 解 　 (1) 函数 f ( x ) 的定义域为 ( － ∞ ，＋ ∞ ) ，且 a ≤ 0. f ′( x ) ＝ 2e 2 x － a e x － a 2 ＝ (2e x ＋ a )(e x － a ). ① 若 a ＝ 0 ，则 f ( x ) ＝ e 2 x ，在 ( － ∞ ，＋ ∞ ) 上单调递增 . 考点一　讨论函数的单调性 【例 1 】 (2017· 全国 Ⅰ 卷改编 ) 已知函数 f ( x ) ＝ e x (e x － a ) － a 2 x ，其中参数 a ≤ 0. (2) ① 当 a ＝ 0 时， f ( x ) ＝ e 2 x ≥ 0 恒成立 . 规律方法　 1.(1) 研究含参数的函数的单调性，要依据参数对不等式解集的影响进行分类讨论 . (2) 划分函数的单调区间时，要在函数定义域内讨论，还要确定导数为 0 的点和函数的间断点 . 2. 个别导数为 0 的点不影响所在区间的单调性，如 f ( x ) ＝ x 3 ， f ′( x ) ＝ 3 x 2 ≥ 0( f ′( x ) ＝ 0 在 x ＝ 0 时取到 ) ， f ( x ) 在 R 上是增函数 . 【训练 1 】 已知函数 f ( x ) ＝ ax ＋ ln x ( a ∈ R ). (1) 若 a ＝ 2 ，求曲线 y ＝ f ( x ) 在 x ＝ 1 处的切线方程； (2) 求 f ( x ) 的单调区间 . 所以切线方程为 y － 2 ＝ 3( x － 1) ，即 3 x － y － 1 ＝ 0. 故曲线 y ＝ f ( x ) 在 x ＝ 1 处的切线方程为 3 x － y － 1 ＝ 0. ① 当 a ≥ 0 时，由于 x >0 ，故 ax ＋ 1>0 ， f ′( x )>0 ， 所以 f ( x ) 的单调递增区间 (0 ，＋ ∞ ). 考点二　根据函数单调性求参数　 典 例迁移 (1) 若函数 h ( x ) ＝ f ( x ) － g ( x ) 存在单调递减区间，求实数 a 的取值范围； (2) 若函数 h ( x ) ＝ f ( x ) － g ( x ) 在 [1 ， 4] 上单调递减，求实数 a 的取值范围 . (1) 若函数 h ( x ) 在 (0 ，＋ ∞ ) 上存在单调减区间， 当且仅当 x ＝ 4 时等号成立 . ∴ h ( x ) 在 [1 ， 4] 上为减函数 . 【迁移 1 】 本例 (2) 中，若函数 h ( x ) ＝ f ( x ) － g ( x ) 在 [1 ， 4] 上单调递增，求 a 的取值范围 . 解　 因为 h ( x ) 在 [1 ， 4] 上单调递增 ， 所以当 x ∈ [1 ， 4] 时， h ′( x ) ≥ 0 恒成立 ， 【迁移 2 】 本例 (2) 中，若函数 h ( x ) 在区间 [1 ， 4] 上不单调，求实数 a 的取值范围 . 解　 ∵ h ( x ) 在区间 [1 ， 4] 上不单调 ， ∴ h ′( x ) ＝ 0 在开区间 (1 ， 4) 上有解 . 规律方法　 1.(1) 已知函数的单调性，求参数的取值范围，应用条件 f ′( x ) ≥ 0( 或 f ′( x ) ≤ 0) ， x ∈ ( a ， b ) 恒成立，解出参数的取值范围 ( 一般可用不等式恒成立的理论求解 ) ，应注意参数的取值是 f ′( x ) 不恒等于 0 的参数的范围 .(2) 如果能分离参数，则尽可能分离参数后转化为参数值与函数最值之间的关系 . 2. 若函数 y ＝ f ( x ) 在区间 ( a ， b ) 上不单调，则转化为 f ′( x ) ＝ 0 在 ( a ， b ) 上有解 . 故实数 m 的取值范围是 ( － ∞ ， 2]. 考点三　函数单调性的简单应用　 多 维探究 角度 1 　比较大小 因为当 x >0 时， xf ′( x ) － f ( x )<0 ，所以 g ′( x )<0. 所以 g ( x ) 在 (0 ，＋ ∞ ) 上是减函数 . 由 f ( x ) 为奇函数，知 g ( x ) 为偶函数，则 g ( － 3) ＝ g (3) ， 又 a ＝ g (e) ， b ＝ g (ln 2) ， c ＝ g ( － 3) ＝ g (3) ， 所以 g (3)< g (e)< g (ln 2) ， 答案　 (1)B 　 (2)D 角度 2 　解不等式 ∴ g ′( x )<0 ，则 g ( x ) 在 ( － ∞ ，＋ ∞ ) 上是减函数 . 由 f ( － 2) ＝ 2 ，且 f ( x ) 在 R 上是奇函数， 规律方法　 1. 利用导数比较大小，其关键在于利用题目条件构造辅助函数，把比较大小的问题转化为先利用导数研究函数的单调性，进而根据单调性比较大小 . 2. 与抽象函数有关的不等式，要充分挖掘条件关系，恰当构造函数；题目中若存在 f ( x ) 与 f ′( x ) 的不等关系时，常构造含 f ( x ) 与另一函数的积 ( 或商 ) 的函数，与题设形成解题链条，利用导数研究新函数的单调性，从而求解不等式 . 【训练 3 】 (1) ( 角度 1) 已知 f ( x ) 是定义在区间 (0 ，＋ ∞ ) 内的函数，其导函数为 f ′( x ) ，且不等式 xf ′( x )<2 f ( x ) 恒成立，则 ( 　　 ) A.4 f (1)< f (2) B.4 f (1)> f (2) C. f (1)<4 f (2) D. f (1)>4 f ′(2) (2) ( 角度 2) f ( x ) 是定义在 R 上的偶函数，当 x ≥ 0 时， f ′( x )>2 x . 若 f ( a － 2) － f ( a ) ≥ 4 － 4 a ，则实数 a 的取值范围是 ( 　　 ) A.( － ∞ ， 1] B.[1 ，＋ ∞ ) C.( － ∞ ， 2] D.[2 ，＋ ∞ ) (2) 令 G ( x ) ＝ f ( x ) － x 2 ，则 G ′( x ) ＝ f ′( x ) － 2 x . 当 x ∈ [0 ，＋ ∞ ) 时， G ′( x ) ＝ f ′( x ) － 2 x >0. ∴ G ( x ) 在 [0 ，＋ ∞ ) 上是增函数 . 由 f ( a － 2) － f ( a ) ≥ 4 － 4 a ，得 f ( a － 2) － ( a － 2) 2 ≥ f ( a ) － a 2 ，即 G ( a － 2) ≥ G ( a ) ， 又 f ( x ) 是定义在 R 上的偶函数，知 G ( x ) 是偶函数 . 故 | a － 2| ≥ | a | ，解之得 a ≤ 1. 答案　 (1)B 　 (2)A