2020版高中数学 第三章 不等式同步精选测试
同步精选测试 二元一次不等式(组)所表示的平面区域
(建议用时:45分钟)
[基础测试]
一、选择题
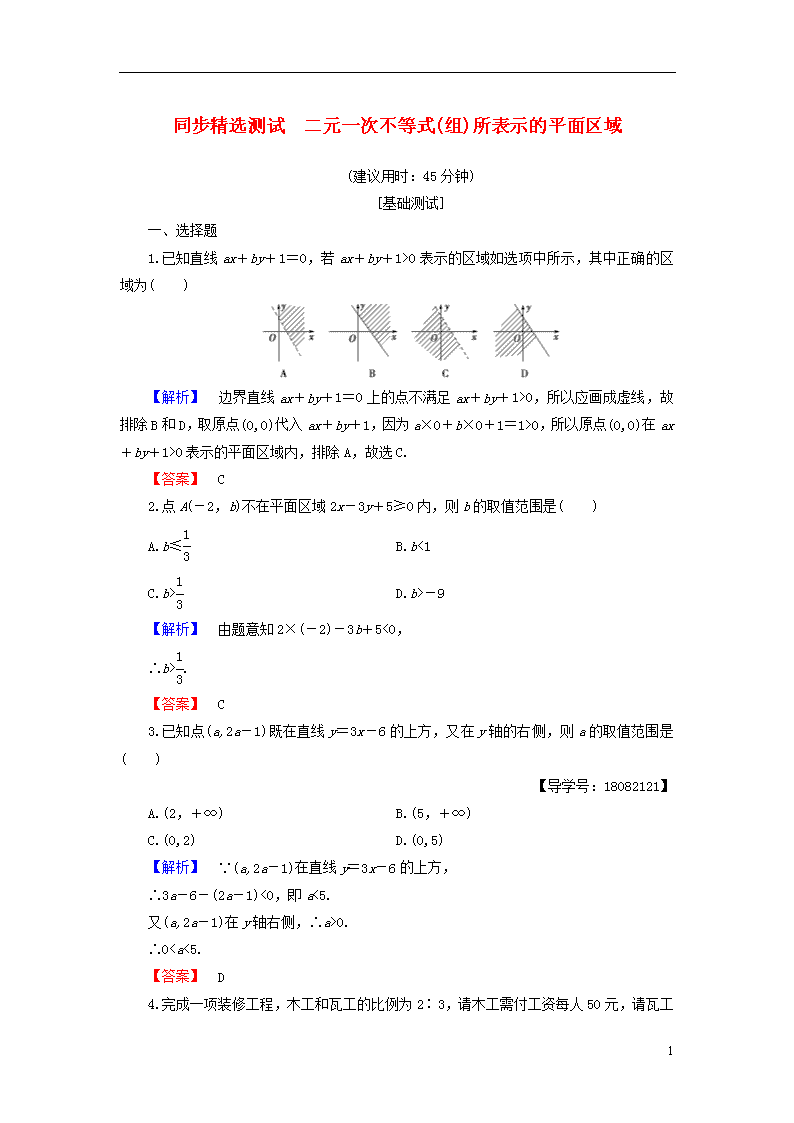
1.已知直线ax+by+1=0,若ax+by+1>0表示的区域如选项中所示,其中正确的区域为( )
【解析】 边界直线ax+by+1=0上的点不满足ax+by+1>0,所以应画成虚线,故排除B和D,取原点(0,0)代入ax+by+1,因为a×0+b×0+1=1>0,所以原点(0,0)在ax+by+1>0表示的平面区域内,排除A,故选C.
【答案】 C
2.点A(-2,b)不在平面区域2x-3y+5≥0内,则b的取值范围是( )
A.b≤ B.b<1
C.b> D.b>-9
【解析】 由题意知2×(-2)-3b+5<0,
∴b>.
【答案】 C
3.已知点(a,2a-1)既在直线y=3x-6的上方,又在y轴的右侧,则a的取值范围是( )
【导学号:18082121】
A.(2,+∞) B.(5,+∞)
C.(0,2) D.(0,5)
【解析】 ∵(a,2a-1)在直线y=3x-6的上方,
∴3a-6-(2a-1)<0,即a<5.
又(a,2a-1)在y轴右侧,∴a>0.
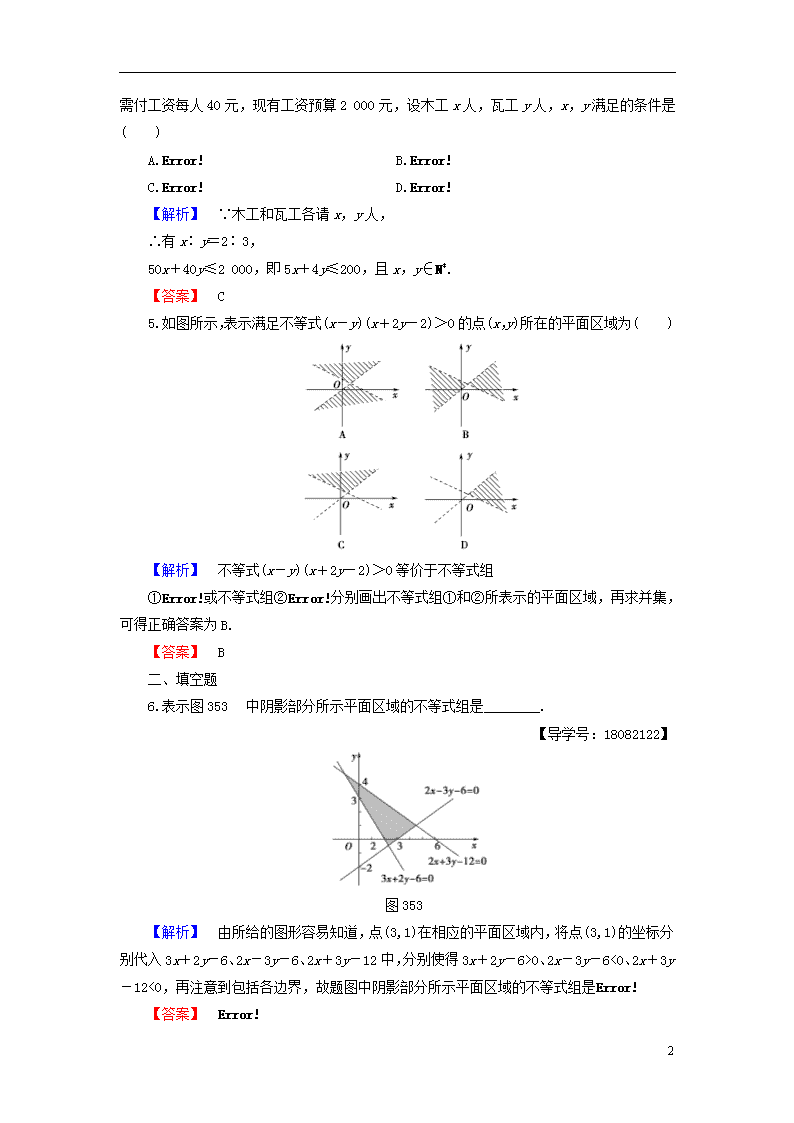
∴0
0、2x-3y-6<0、2x+3y-12<0,再注意到包括各边界,故题图中阴影部分所示平面区域的不等式组是
【答案】
6
7.原点(0,0)与点(1,1)有且仅有一个点在不等式2x-y+a>0表示的平面区域内,则a的取值范围为________.
【解析】 根据题意,分以下两种情况:
①原点(0,0)在该区域内,点(1,1)不在该区域内.则无解.
②原点(0,0)不在该区域内,点(1,1)在该区域内,则∴-1<a≤0.
综上所述,a的取值范围是(-1,0].
【答案】 (-1,0]
8.若不等式组表示的平面区域为Ω,则当a从-2连续变化到1时,动直线x+y-a=0扫过Ω中的那部分区域的面积为________.
【解析】 如图所示,Ω为△BOE所表示的区域,而动直线x+y=a扫过Ω中的那部分区域为四边形BOCD,而B(-2,0),O(0,0),C(0,1),D,E(0,2),△CDE为直角三角形,∴S四边形BOCD=S△BOE-S△CDE=×2×2-×1×=.
【答案】
三、解答题
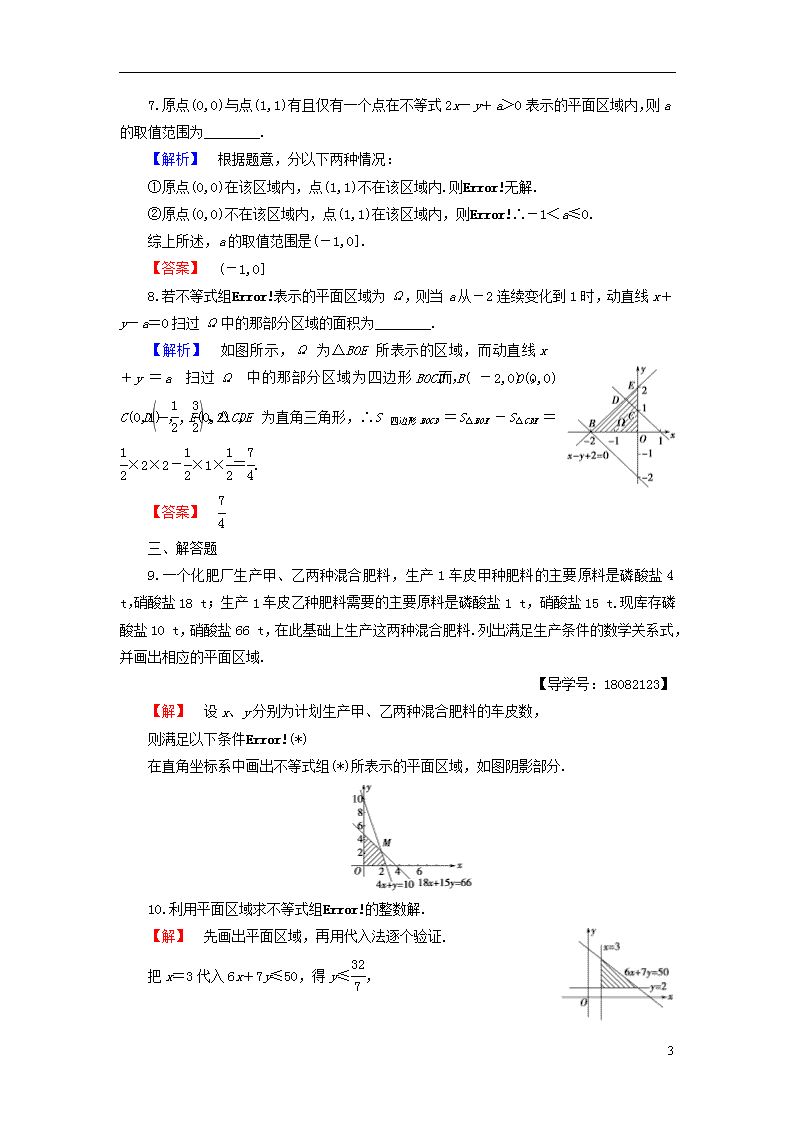
9.一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4 t,硝酸盐18 t;生产1车皮乙种肥料需要的主要原料是磷酸盐1 t,硝酸盐15 t.现库存磷酸盐10 t,硝酸盐66 t,在此基础上生产这两种混合肥料.列出满足生产条件的数学关系式,并画出相应的平面区域.
【导学号:18082123】
【解】 设x、y分别为计划生产甲、乙两种混合肥料的车皮数,
则满足以下条件(*)
在直角坐标系中画出不等式组(*)所表示的平面区域,如图阴影部分.
10.利用平面区域求不等式组的整数解.
【解】 先画出平面区域,再用代入法逐个验证.
把x=3代入6x+7y≤50,得y≤,
又∵y≥2,∴整点有(3,2),(3,3),(3,4);
6
把x=4代入6x+7y≤50,得y≤,
∴整点有(4,2),(4,3).
把x=5代入6x+7y≤50,得y≤,
∴整点有(5,2);
把x=6代入6x+7y≤50,得y≤2,整点有(6,2);
把x=7代入6x+7y≤50,
得y≤,与y≥2不符.
∴整数解共有7个为(3,2),(3,3),(3,4),(4,2),(4,3),(5,2),(6,2).
[能力提升]
1.若不等式组表示的平面区域是一个三角形,则a的取值范围是( )
A.(5,7) B.[5,7)
C.[5,7] D.(5,7]
【解析】 不等式组表示的平面区域如图所示,当y=a过A(0,5)时表示的平面区域为三角形,即△ABC,当5
查看更多