高中数学第8章圆锥曲线方程（第15课时）抛物线的简单几何性质(1)

高中数学第8章圆锥曲线方程（第15课时）抛物线的简单几何性质(1)

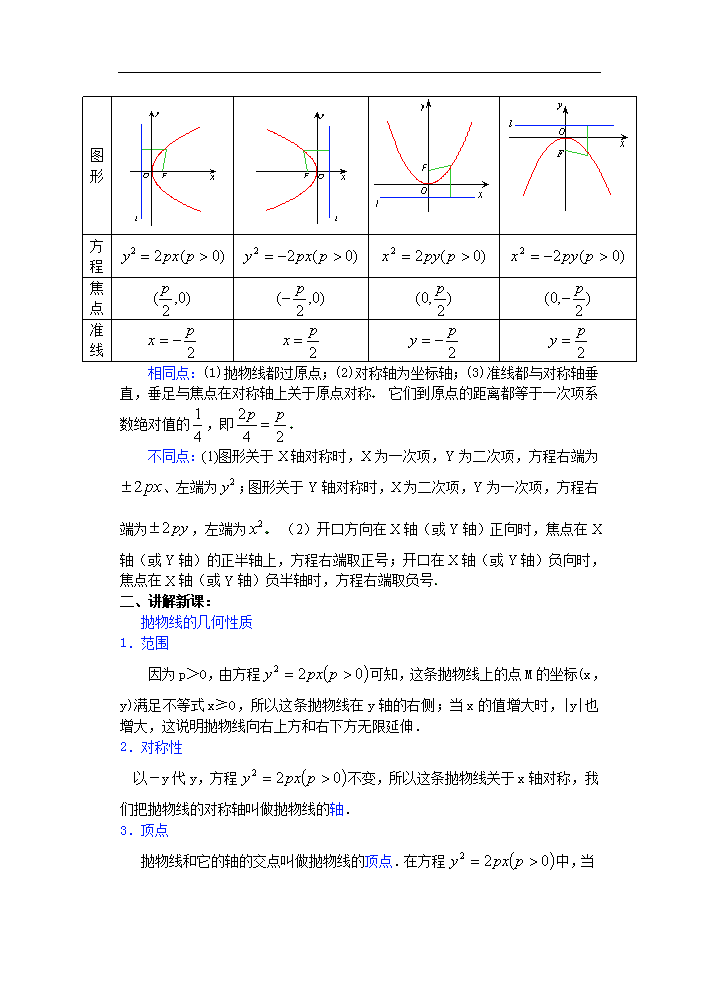
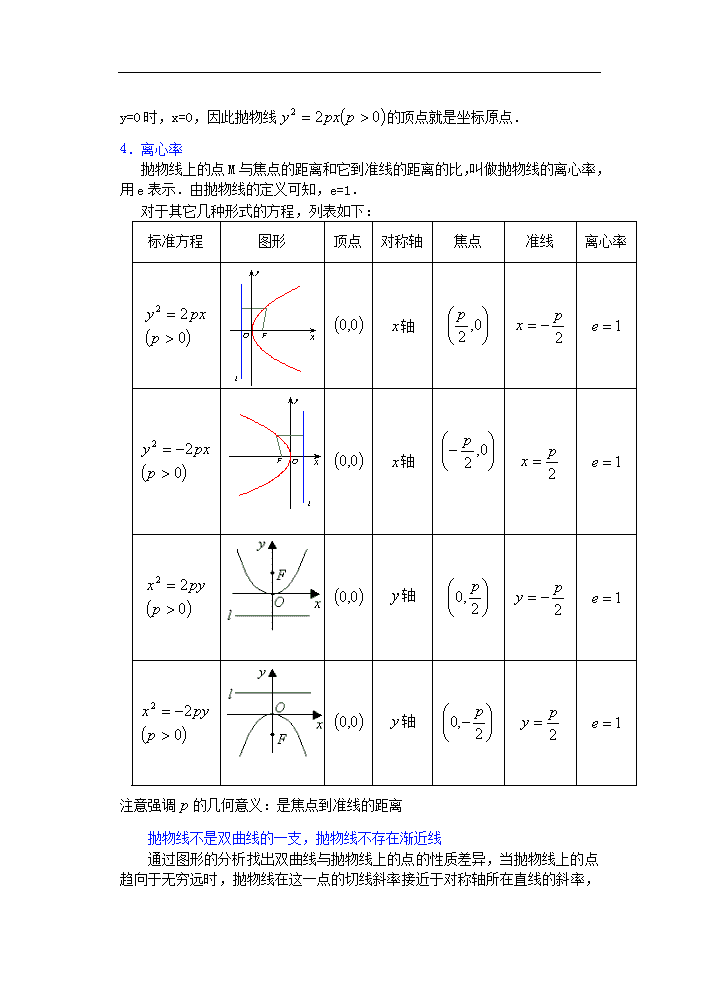
课 题：8．6抛物线的简单几何性质（一）‎ 教学目的：‎ ‎1．掌握抛物线的范围、对称性、顶点、离心率等几何性质；‎ ‎2．能根据抛物线的几何性质对抛物线方程进行讨论，在此基础上列表、描点、画抛物线图形；‎ ‎3．在对抛物线几何性质的讨论中，注意数与形的结合与转化 ‎ 教学重点：抛物线的几何性质及其运用 教学难点：抛物线几何性质的运用 ‎ 授课类型：新授课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 内容分析：   “抛物线的简单几何性质”是课本第八章最后一节，它在全章占有重要的地位和作用本节知识在生产、生活和科学技术中经常用到，也是大纲规定的必须掌握的内容，还是将来大学学习的基础知识之一 对于训练学生用坐标法解题，本节一如前面各节一样起着相当重要的作用 研究抛物线的几何性质和研究椭圆、双曲线的几何性质一样，按范围、对称性、顶点、离心率顺序来研究，完全可以独立探索得出结论 已知抛物线的标准方程，求它的焦点坐标和准线方程时，首先要判断抛物线的对称轴和开口方向，一次项的变量如果为（或），则轴（或轴）是抛物线的对称轴，一次项的符号决定开口方向，由已知条件求抛物线的标准方程时，首先要根据已知条件确定抛物线标准方程的类型，再求出方程中的参数 ‎ 本节分两课时进行教学 第一课时内容主要讲抛物线的四个几何性质、抛物线的画图、例1、例2、及其它例题；第二课时主要内容焦半径公式、通径、例3‎ 教学过程：‎ 一、复习引入： ‎ ‎1．抛物线定义：‎ 平面内与一个定点F和一条定直线的距离相等的点的轨迹叫做抛物线 定点F叫做抛物线的焦点，定直线叫做抛物线的准线 ‎ ‎2．抛物线的标准方程： ‎ 图形 方程 焦点 准线 相同点：(1)抛物线都过原点；(2)对称轴为坐标轴；(3)准线都与对称轴垂直，垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的，即 ‎ 不同点：(1)图形关于X轴对称时，X为一次项，Y为二次项，方程右端为、左端为；图形关于Y轴对称时，X为二次项，Y为一次项，方程右端为，左端为 （2）开口方向在X轴（或Y轴）正向时，焦点在X轴（或Y轴）的正半轴上，方程右端取正号；开口在X轴（或Y轴）负向时，焦点在X轴（或Y轴）负半轴时，方程右端取负号 ‎ 二、讲解新课：‎ 抛物线的几何性质 ‎1．范围 因为p＞0，由方程可知，这条抛物线上的点M的坐标(x，y)满足不等式x≥0，所以这条抛物线在y轴的右侧；当x的值增大时，|y|也增大，这说明抛物线向右上方和右下方无限延伸．‎ ‎2．对称性 以－y代y，方程不变，所以这条抛物线关于x轴对称，我们把抛物线的对称轴叫做抛物线的轴．‎ ‎3．顶点 抛物线和它的轴的交点叫做抛物线的顶点．在方程 中，当y=0时，x=0，因此抛物线的顶点就是坐标原点．‎ ‎4．离心率 抛物线上的点M与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e表示．由抛物线的定义可知，e=1．‎ 对于其它几种形式的方程，列表如下：‎ 标准方程 图形 顶点 对称轴 焦点 准线 离心率 轴 轴 轴 轴 注意强调的几何意义：是焦点到准线的距离 抛物线不是双曲线的一支，抛物线不存在渐近线 通过图形的分析找出双曲线与抛物线上的点的性质差异，当抛物线上的点趋向于无穷远时，抛物线在这一点的切线斜率接近于对称 轴所在直线的斜率，也就是说接近于和对称轴所在直线平行，而双曲线上的点趋向于无穷远时，它的切线斜率接近于其渐近线的斜率 ‎ 附：抛物线不存在渐近线的证明．（反证法）‎ 假设抛物线y2＝2px存在渐近线y＝mx＋n，A（x，y）为抛物线上一点，‎ A0（x，y1）为渐近线上与A横坐标相同的点如图，‎ 则有和y1＝mx＋n．‎ ‎∴ ‎ 当m≠0时，若x→＋∞，则 当m＝0时，，当x→＋∞，则 这与y＝mx＋n是抛物线y2＝2px的渐近线矛盾，所以抛物线不存在渐近线 三、讲解范例：‎ 例1 已知抛物线关于x轴为对称，它的顶点在坐标原点，并且经过点，求它的标准方程，并用描点法画出图形．‎ 分析：首先由已知点坐标代入方程，求参数p．‎ 解：由题意，可设抛物线方程为，因为它过点，‎ 所以 ，即 ‎ 因此，所求的抛物线方程为．‎ 将已知方程变形为，根据计算抛物线在的范围内几个点的坐标，得 x ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎0‎ ‎2‎ ‎2.8‎ ‎3.5‎ ‎4‎ ‎…‎ 描点画出抛物线的一部分，再利用对称性，就可以画出抛物线的另一部分 点评：‎ 在本题的画图过程中，如果描出抛物线上更多的点，可以发现这条抛物线虽然也向右上方和右下方无限延伸，但并不能像双曲线那样无限地接近于某一直线，也就是说，抛物线没有渐近线．‎ 例2 探照灯反射镜的轴截面是抛物线的一部分，光源位于抛物线的焦点处，已知灯的圆的直径60cm，灯深为40cm，求抛物线的标准方程和焦点位置．‎ 分析：这是抛物线的实际应用题，设抛物线的标准方程后，根据题设条件，可确定抛物线上一点坐标，从而求出p值．‎ 解：如图，在探照灯的轴截面所在平面内建立直角坐标系，使反光镜的顶点(即抛物线的顶点)与原点重合，x轴垂直于灯口直径．‎ 设抛物线的标准方程是 (p＞0)．‎ 由已知条件可得点A的坐标是(40，30)，代入方程，得，‎ 即 ‎ 所求的抛物线标准方程为．‎ 例3 过抛物线的焦点F任作一条直线m，交这抛物线于A、B两点，‎ 求证：以AB为直径的圆和这抛物线的准线相切．‎ 分析：运用抛物线的定义和平面几何知识来证比较简捷．‎ 证明：如图．设AB的中点为E，过A、E、B分别向准线引垂线AD，EH，BC，垂足为D、H、C，则 ‎｜AF｜＝｜AD｜，｜BF｜＝｜BC｜‎ ‎∴｜AB｜＝｜AF｜＋｜BF｜＝｜AD｜＋｜BC｜＝2｜EH｜‎ 所以EH是以AB为直径的圆E的半径，且EH⊥l，因而圆E和准线相切．‎ 四、课堂练习：‎ ‎1．过抛物线的焦点作直线交抛物线于，两点，如果，那么=（ B ）‎ ‎（A）10 （B）8 （C）6 （D）4‎ ‎2．已知为抛物线上一动点，为抛物线的焦点，定点，则的最小值为（ B ）‎ ‎（A）3 （B）4 （C）5 （D）6‎ ‎3．过抛物线的焦点作直线交抛物线于、两点，若线段 ‎、的长分别是、，则=（ C ）‎ ‎（A） （B） （C） （D）‎ ‎4．过抛物线焦点的直线它交于、两点，则弦的中点的轨迹方程是 ______ (答案： ) ‎ ‎5.定长为的线段的端点、在抛物线上移动，求中点到轴距离的最小值，并求出此时中点的坐标 ‎（答案： , M到轴距离的最小值为）‎ 五、小结 ：抛物线的离心率、焦点、顶点、对称轴、准线、中心等 ‎ 六、课后作业：‎ ‎1．根据下列条件，求抛物线的方程，并画出草图．‎ ‎（1）顶点在原点，对称轴是x轴，顶点到焦点的距离等于8．‎ ‎（2）顶点在原点，焦点在y轴上，且过P（4，2）点．‎ ‎（3）顶点在原点，焦点在y轴上，其上点P（m，－3）到焦点距离为5．‎ ‎2．过抛物线焦点F的直线与抛物线交于A、B两点，若A、B在准线上的射影是A2，B2，则∠A2FB2等于　　　　　　　‎ ‎3．抛物线顶点在原点，以坐标轴为对称轴，过焦点且与y轴垂直的弦长为16，求抛物线方程．‎ ‎4．以椭圆的右焦点，F为焦点，以坐标原点为顶点作抛物线，求抛物线截椭圆在准线所得的弦长．‎ ‎5．有一抛物线型拱桥，当水面距拱顶4米时，水面宽40米，当水面下降1米时，水面宽是多少米？‎ 习题答案：‎ ‎1．（1）y2＝±32x （2）x2＝8y （3）x2＝－8y ‎ ‎2．90°‎ ‎3．x2＝±16 y ‎ ‎4．‎ ‎5．米 七、板书设计（略）‎ 八、课后记： ‎