数学文卷·2019届甘肃省武威市第六中学高二下学期寒假学习质量检测（2018-02）

数学文卷·2019届甘肃省武威市第六中学高二下学期寒假学习质量检测（2018-02）

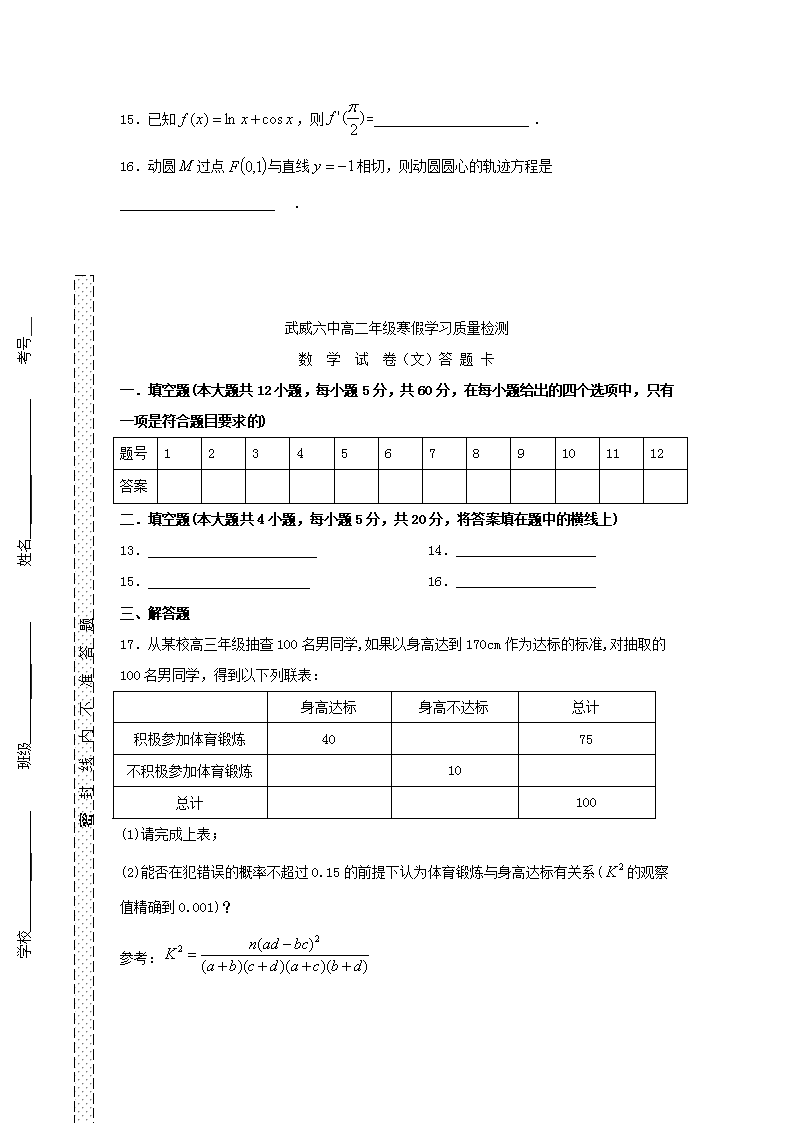
武威六中高二年级寒假学习质量检测 数 学 试 卷（文）‎ 一、选择题 ‎1．“”是“”的 A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎2．下表是某厂1—4月份用水量(单位：百吨)的一组数据：‎ 月份 ‎1‎ ‎2‎ ‎3‎ ‎4‎ 用水量 ‎4.5‎ ‎4‎ ‎3‎ ‎2.5‎ 由散点图可知，用水量与月份之间有较好的线性相关关系，其线性回归方程为 ‎，则等于 A．10.5 B．5.15 C．5.2 D．5.25‎ ‎3．双曲线的两个焦点分别是，，双曲线上一点到焦点的距离是 ‎12，则点到焦点的距离是 A．17 B．7 C．7或17 D．2或22‎ ‎4．过点(3,0)且与轴相切的圆的圆心的轨迹为 ‎ A．圆 B．椭圆 C．直线 D．抛物线 ‎5．已知椭圆C的左、右焦点坐标分别是(-,0),(,0),离心率是，则椭圆C的 方程为 ‎ A． B． C． D．‎ ‎6．设抛物线上一点到轴的距离是4，则点到该抛物线焦点的距离是 ‎ A．4 B．6 C．8 D．12‎ ‎7．抛物线的准线方程是 A． B． C． D． ‎8．若是2和8的等比中项,则圆锥曲线的离心率为 A． B． C．或 D．或 ‎9．函数在区[-4，4]上的最大值为 A．10 B．-71 C．-15 D．-22 ‎10．抛物线上的点到直线距离的最小值是 ‎ A． B． C． D．3‎ ‎11．在平面直角坐标系中，是椭圆上的一个动点，点（1,1），（0,1），‎ 则的最大值为 A．5 B．4 C．3 D．2‎ ‎12．设是函数的导函数，的图象如图所示，则的图象最有可能的是 二、填空题 ‎13．命题“任意两个等边三角形都全等”的否定是　　　　　　　. ‎ ‎14．设中心在原点的椭圆与双曲线有公共的焦点，且它们的离心率互为倒数，则该椭圆的方程为_____________.‎ ‎15．已知，则=            .‎ ‎16．动圆过点与直线相切，则动圆圆心的轨迹方程是             .‎ 学校 ____ 班级 _____ 姓名 _______ 考号______________ ‎ 密 封 线 内 不 准 答 题 武威六中高二年级寒假学习质量检测 数 学 试 卷（文）答 题 卡 一．填空题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二．填空题(本大题共4小题，每小题5分，共20分，将答案填在题中的横线上)‎ ‎13． 14．____________________‎ ‎15． 16．____________________‎ 三、解答题 ‎17．从某校高三年级抽查100名男同学,如果以身高达到170cm作为达标的标准,对抽取的100名男同学，得到以下列联表：‎ 身高达标 身高不达标 总计 积极参加体育锻炼 ‎40‎ ‎75‎ 不积极参加体育锻炼 ‎10‎ 总计 ‎100‎ ‎(1)请完成上表；‎ ‎(2)能否在犯错误的概率不超过0.15的前提下认为体育锻炼与身高达标有关系(的观察值精确到0.001)？‎ 参考：‎ ‎0.15‎ ‎0.10‎ ‎2. 072‎ ‎2.706‎ ‎18．已知命题表示焦点在轴上的椭圆，命题 表示双曲线；或为真，且为假，求的取值范围.‎ ‎19．抛物线顶点在原点，焦点在轴上，且过点(4,4)焦点为；‎ ‎(1)求抛物线的焦点坐标和标准方程；‎ ‎(2) 是抛物线上一动点，点是的中点，求点的轨迹方程.‎ ‎20．已知函数在处取得极值.‎ ‎(1)求常数的值；‎ ‎(2)求函数的单调区间与极值.‎ ‎21．在平面直角坐标系，动点到两点的距离之和等于4，设点的轨迹为曲线，直线过点(-1,0)且与曲线交于两点.‎ ‎(1)求曲线的轨迹方程；‎ ‎(2)Δ的面积是否存在最大值?若存在,求出Δ的面积；若不存在，说明理由.‎ ‎22．已知函数.‎ ‎(1)若函数的图象在处的切线斜率为1，求实数的值；‎ ‎(2)在(1)的条件下，求函数的单调区间；‎ ‎(3)若函数在上是减函数，求实数的取值范围.‎