上海教育高中数学三上旋转体的概念

上海教育高中数学三上旋转体的概念

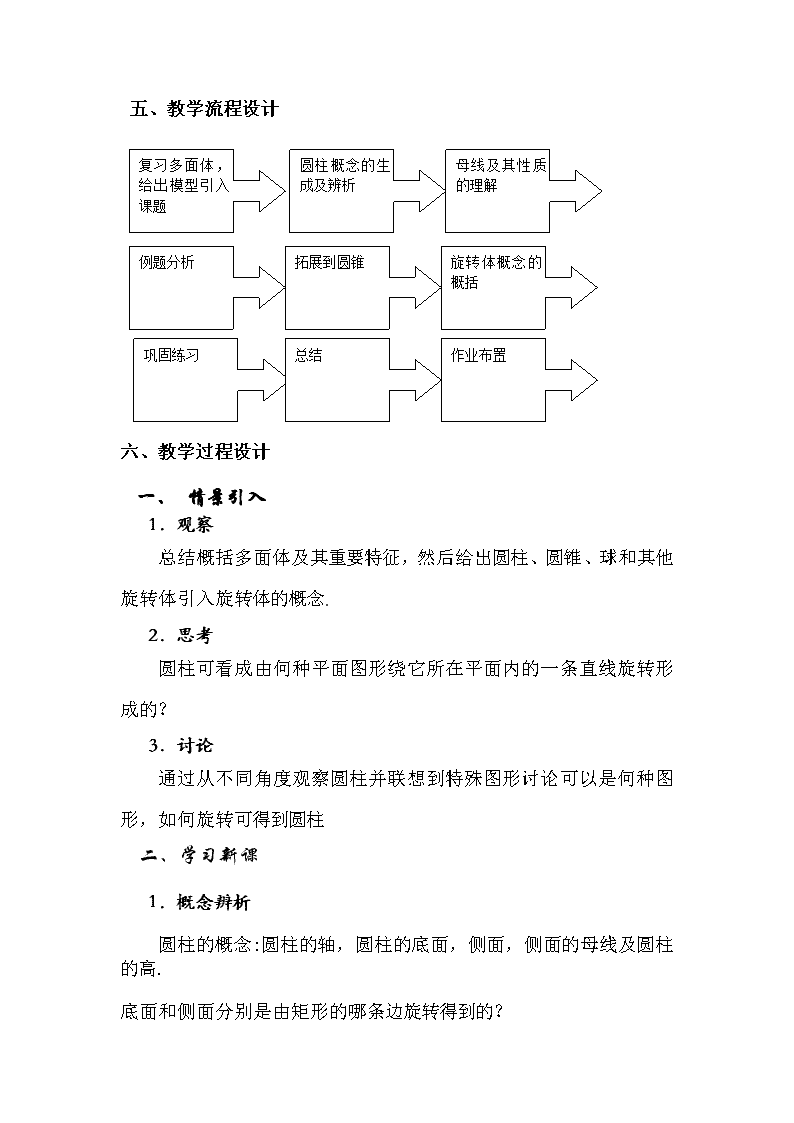
‎15.3旋转体的概念（1）‎ 一、教学内容分析 本节课是在学习完棱柱、棱锥两种特殊的多面体之后，学习的第二类简单的几何体，圆柱与圆锥学生已经有所接触，但只是生活意义上的理解，课本这里是给出数学定义.圆柱与圆锥内容的承上之处是它们与棱柱、棱锥都是由四边形或三角形构成的，区别在于构成的方式不同，这里学生认知上的一个重要发展是曲面的概念及其形成的数学理解.而这一发展又正好是对球的概念及所有旋转体的概念的形成起到了启下作用，是学生后序发展的最近发展区.‎ 二、教学目标设计 ‎1、理解圆柱、圆锥及其有关概念的形成过程；‎ ‎2、理解圆柱、圆锥的侧面的母线的概念及母线之间的关系，母线所具有的性质；‎ ‎3、通过对圆柱、圆锥的研究培养空间想象力及知识的自我生成和发展能力.‎ 三、教学重点及难点 ‎ 重点是圆柱、圆锥概念的生成；难点是母线及其相关性质的理解和简单应用.‎ 四、教学用具准备 教具、学具：圆柱，圆锥实物模型、多媒体设备（宋体四号）‎ 复习多面体，给出模型引入课题 母线及其性质的理解 圆柱概念的生成及辨析 例题分析 拓展到圆锥 旋转体概念的概括 巩固练习 总结 作业布置 五、教学流程设计 六、教学过程设计 ‎ 一、 情景引入 ‎ 1．观察 总结概括多面体及其重要特征，然后给出圆柱、圆锥、球和其他旋转体引入旋转体的概念.‎ ‎ 2．思考 圆柱可看成由何种平面图形绕它所在平面内的一条直线旋转形成的？‎ ‎ 3．讨论 通过从不同角度观察圆柱并联想到特殊图形讨论可以是何种图形，如何旋转可得到圆柱 二、学习新课 ‎ 1．概念辨析 圆柱的概念:圆柱的轴，圆柱的底面，侧面，侧面的母线及圆柱的高.‎ 底面和侧面分别是由矩形的哪条边旋转得到的？‎ 底面由与轴垂直的边旋转得到，所以圆柱的底面是圆面且垂直于轴.‎ 侧面是由与轴平行的边旋转得到，所以侧面是曲面，且该边旋转到任何位置所得到的线段都是侧面的母线，因此母线有无穷多条,互相平且相等.‎ ‎ 2．例题分析 例1用垂直于轴的平面截圆柱，所得截面是何种图形？‎ 例2用平行于轴的平面截圆柱，所得截面是何种图形？‎ 例3把圆柱的侧面沿一条母线展开，所得图形是哪种图形？‎ 可以实物引导学生具体操作，探究并解决问题.‎ ‎ 3．问题拓展 根据对圆柱的学习，你能否研究一下圆锥，得出与圆柱相应的概念、性质，并回答与圆柱的三个例题相对应的问题？‎ 下面可以让学生独立或分组根据实物对圆锥进行研究，教师巡视观察学生的进展情况，并随时给予指导.‎ 最后由学生总结研究结果.‎ 在学习过圆柱和圆锥的基础上引导学生给出旋转体的概念.‎ 三、巩固练习 ‎1、举出生活中的圆柱和圆锥的实例.‎ ‎2、用垂直于圆柱底面的平面截圆柱，何时截面面积最大？最大面积是多少？‎ ‎3、若直角三角形绕其斜边所在直线旋转一周所得几何体是何形状？‎ 四、课堂小结 ‎1、圆柱，圆锥，旋转体的概念，和侧面母线，侧面展开图形状.‎ ‎2、圆柱与圆锥垂直于轴的截面和平行于轴的截面的特点.‎ 五、作业布置 练习册，‎ 拓展作业：‎ ‎1、求过圆锥顶点的截面三角形顶角的最大值和面积的最大值.‎ ‎2、与圆柱和圆锥的轴斜交的平面截圆柱和圆锥所得截面是何种图形？‎ 七、教学设计说明 圆柱、圆锥学生已经有所接触，所以并不陌生，但是学生的经验或知识仅是感性经验，并没有上升到数学的角度，所以对圆柱和圆锥的本质特点往往把握不准.因此本节课在设计时把重点放在从数学的角度观察圆柱和圆锥，揭示其数学特征，并用数学语言表示描述其特征上，让学生体验把感性知识数学化的过程.在练习和作业中的截面问题要求较高，可根据学生的情况控制难度.‎ 另外从知识的呈现次序上，与课本先总后分不同，采用了先分后总的次序，比较符合认识规律.‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com