高中数学必修1教案：第二章（第29课时）函数复习小结2

高中数学必修1教案：第二章（第29课时）函数复习小结2

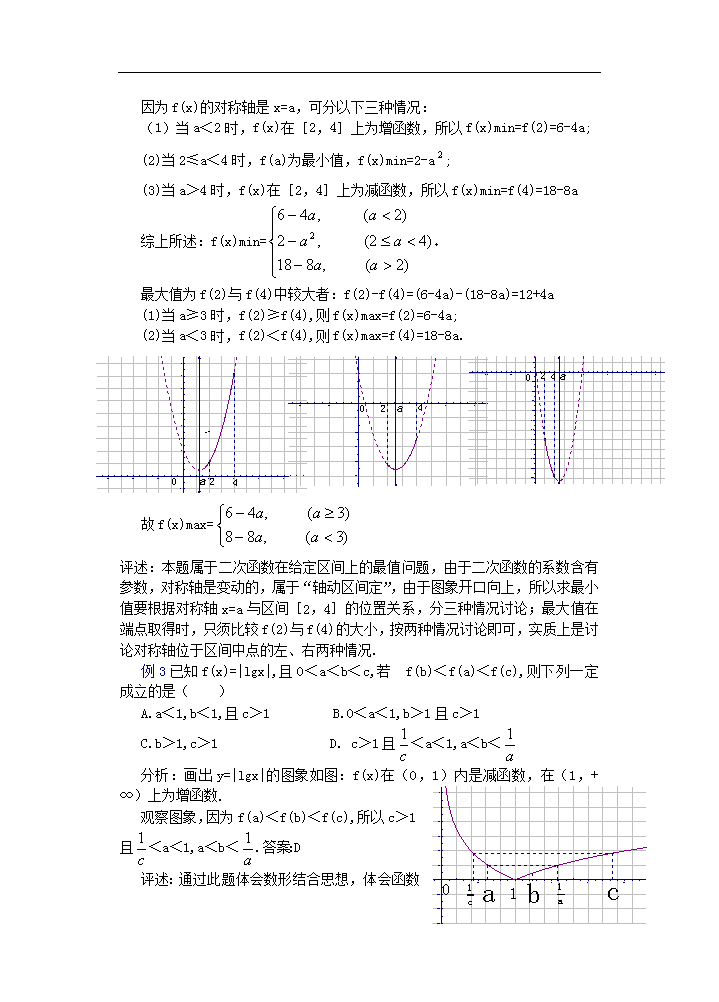
课 题：函数复习小结（二）‎ 教学目的： ‎ ‎1.熟悉并掌握函数的对称语言.‎ ‎2.进一步熟悉二次函数性质及其应用.‎ ‎3.把握数形结合的特征和方法.‎ ‎4.能够应用函数思想解题.‎ ‎5.了解与函数有关的数学模型.‎ 教学重点：数形结合的特征与方法 教学难点：函数思想的应用 授课类型：复习课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程： ‎ 一、引入：‎ 通过上一节学习，大家了解了本章内容的整体结构，明确了本章的重难点知识，并熟悉了有关函数的基本概念和基本方法，这一节，我们将通过例题分析重点掌握数形结合的特征与方法，并进一步认清函数的思想实质，进而掌握其应用.‎ 二、例题分析：‎ 例1若函数f(x)=x+bx+c对任意实数x都有f(2+x)=f(2-x)，那么（ ）‎ A.f(2)＜f(1)＜f(4) B.f(1)＜f(2)＜f(4)‎ C.f(2)＜f(4)＜f(1) D.f(4)＜f(2)＜f(1) ‎ 分析：此题解决的关键是将函数的对称语言转化为对称轴方程.‎ 解：由f(2+x)=f(2-x)可知：函数f(x)的对称轴为x=2,由二次函数f(x)开口方向向，可得f(2)最小，又f(4)=f(2+2)=f(2-2)=f(0)‎ 在x＜2时，y=f(x)为减函数 ‎∵0＜1＜2，∴f(0)＞f(1)＞f(2)‎ 即f(2)＜f(1)＜f(4)答案：A 通过此题可将对称语言推广如下：‎ ‎（1）若对任意实数x,都有f(a+x)=f(a-x)成立，则x=a是函数f(x)的对称轴 ‎（2）若对任意实数x,都有f(a+x)=f(b-x)成立，则x=是f(x)的对称轴.‎ 例2求f(x)=x-2ax+2在［2，4］上的最大值和最小值. ‎ 解：先求最小值.‎ 因为f(x)的对称轴是x=a，可分以下三种情况：‎ ‎（1）当a＜2时，f(x)在［2，4］上为增函数，所以f(x)min=f(2)=6-4a;‎ ‎(2)当2≤a＜4时，f(a)为最小值，f(x)min=2-a;‎ ‎(3)当a＞4时，f(x)在［2，4］上为减函数，所以f(x)min=f(4)=18-8a 综上所述：f(x)min=‎ 最大值为f(2)与f(4)中较大者：f(2)-f(4)=(6-4a)-(18-8a)=12+4a ‎(1)当a≥3时，f(2)≥f(4),则f(x)max=f(2)=6-4a;‎ ‎(2)当a＜3时，f(2)＜f(4),则f(x)max=f(4)=18-8a.‎ 故f(x)max=‎ 评述：本题属于二次函数在给定区间上的最值问题，由于二次函数的系数含有参数，对称轴是变动的，属于“轴动区间定”，由于图象开口向上，所以求最小值要根据对称轴x=a与区间［2，4］的位置关系，分三种情况讨论；最大值在端点取得时，只须比较f(2)与f(4)的大小，按两种情况讨论即可，实质上是讨论对称轴位于区间中点的左、右两种情况.‎ 例3已知f(x)=|lgx|,且0＜a＜b＜c,若f(b)＜f(a)＜f(c),则下列一定成立的是（ ）‎ A.a＜1,b＜1,且c＞1 B.0＜a＜1,b＞1且c＞1‎ C.b＞1,c＞1 D. c＞1且＜a＜1,a＜b＜ ‎ 分析：画出y=|lgx|的图象如图：f(x)在（0，1）内是减函数，在（1，+∞）上为增函数.‎ 观察图象，因为f(a)＜f(b)＜f(c),所以c＞1且＜a＜1,a＜b＜.答案：D 评述：通过此题体会数形结合思想，体会函数图象在函数单调性问题中的应用.‎ 例4函数f(x)=x-bx+c，满足对于任何x∈R都有f(1+x)=f(1-x)，且f(0)=3,则f(b)与f(c)的大小关系是（ ）‎ A.f(b)≤f(c) B.f(b)≥f(c)‎ C.f(b)＜f(c) D.f(b)＞f(c)‎ 分析：由对称语言f(1+x)=f(1-x)可以确定函数对称轴，从而确定b值，再由f(0)=3,可确定c值，然后结合b,c的大小关系及二次函数的单调区间使问题得以解决.‎ 解：∵f(1+x)=f(1-x)∴f(x)的对称轴x=-=1‎ ‎∴b=2,又f(0)=3,∴c=3,‎ ‎∴f(x)=x-2x+3‎ ‎(1)当x＞0时，1＜2＜3,且f(x)在［1，+∞上是增函数 所以f(2)＜f(3),即f(b)＜f(c)‎ ‎(2)当x＜0时，1＞2＞3,且f(x)在（-∞,1）上是减函数，所以f(2)＜f(3)，即f(b)＜f(c)‎ ‎(3)当x=0时，2=3=1‎ 则f(2)=f(3),即f(b)=f(c)‎ 综上所述，f(b)≤f(c).‎ 答案：A 三、课堂练习：‎ 已知f(x)=x-4x-4,x∈［t,t+1］(t∈R)，求f(x)的最小值φ（t）的解析式.‎ 解：f(x)=(x-2)-8‎ ‎(1)当2∈［t,t+1］时，即1＜t＜2时，φ(t)=f(2)=-8.‎ ‎(2)当t＞2时，f(x)在［t,t+1］上是增函数，故φ(t)=f(t)=t-4t-4.‎ ‎(3)当t+1＜2，即t＜1时，f(x)在［t,t+1］上是减函数.‎ 故φ(t)=f(t+1)=t-2t-7‎ 综上所述：φ(t)= ‎ 四、课时小结：‎ 本节学习了二次函数在给定区间上求最值的方法，把握数形结合的特征与方法，逐步掌握函数思想在实际问题中的应用.‎ 五、课后作业：‎ ‎1.某农工贸集团开发的养殖业和养殖加工生产业的年利润分别是T和Q（万元），这两项生产与投入的奖金a(万元)的关系是P=，该集团今年计划对这两项生产共投入奖金60万元，为获得最大利润，对养殖业与养殖加工生产业投入应各为多少万元？最大利润为多少万元？‎ 解：设投入养殖业为x万元，则投入养殖加工生产业为60-x万元 由题意：P+Q= (0≤x≤60)‎ 设t=,则0≤t≤,x=60-t P+Q=(60-t)+t=-(t-5)+ ‎ ‎∴当t=5时，即x=35时，（P+Q）max=.‎ ‎∴对养殖业投入35万元，对养殖加工生产业投入25万元，可获最大利润万元.‎ ‎2.已知，求函数的最大值和最小值，并求取最大值和最小值的相应的的值 答案：时，取最大值13；时，取最小值6‎ ‎3.设集合,，函数 ‎（1）设不等式的解集为C，当时，求实数的取值范围；‎ ‎（2）若对任意实数，均有恒成立，求时，的值域；‎ ‎（3）当时，证明 答案：（1） （2）‎ ‎（3）因为对称轴，‎ 故只需证明，，即可 十二、板书设计（略）‎ 十三、课后记：‎