- 2021-06-20 发布 |
- 37.5 KB |
- 3页


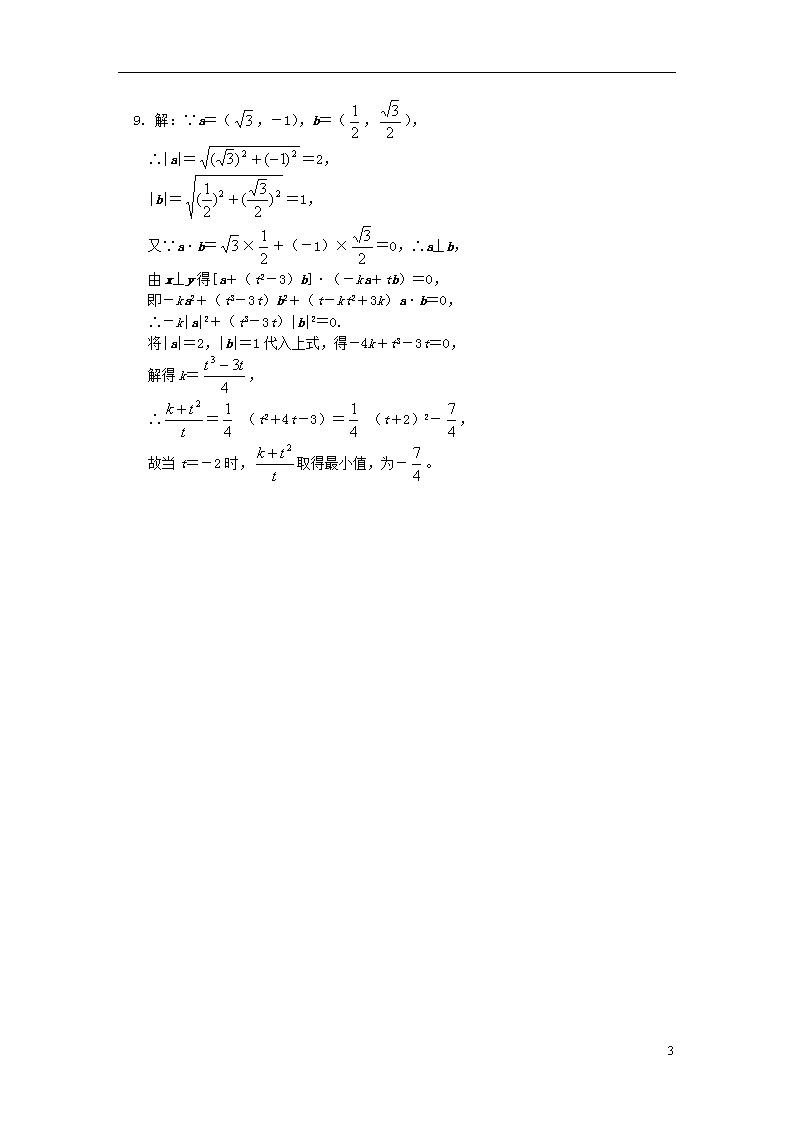
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 第2章 平面向量 第四讲 向量的数量积习题 苏教版必修4
向量的数量积 (答题时间:40分钟) 1. 下列式子: ①=;②(a·b)2=a2·b2;③a·a·a=a3;④(a·b)·c=a·(b·c) 其中错误的序号为________。 *2. (安徽高考)若非零向量a,b满足|a|=3|b|=|a+2b|,则a与b夹角的余弦值为_______。 **3. (山东高考)在平面直角坐标系xOy中,已知=(-1,t),=(2,2),若∠ABO=90°,则实数t的值为________。 *4. 在边长为1的正三角形ABC中,设=2,=3,则·=________。 **5. 已知向量a=(1,2),b=(-2,-4),|c|=,若(a+b)·c=,则a与c的夹角是________。 **6. 已知向量=(2,2),=(4,1),O为坐标原点,在x轴上取一点P使·有最小值,则点P的坐标是________。 **7. 已知|a|=5,|b|=4,且a与b的夹角为60°,则当k为何值时,向量ka-b与a+2b垂直? **8. 已知|a|=,|b|=3,a和b的夹角为45°,求当向量a+λb与a+b的夹角为锐角时λ的取值范围。 ***9. 已知a=(,-1),b=(,),且存在实数k和t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,试求的最小值。 3 1. ①②④ 解析:①错,因为不存在这样的运算,向量间只能作加、减、乘运算,此题应分子、分母先分开算;②错,因为(a·b)2=(|a|·|b|cos θ)2=a2·b2cos2θ不一定与a2·b2相等;④错,因为a与c方向未必一致。 2. - 解析:由|a|=|a+2b|,两边平方,得|a|2=(a+2b)2=|a|2+4|b|2+4a·b,所以a·b=-|b|2,又|a|=3|b|,所以cos〈a,b〉===-。 3. 5 解析:∵∠ABO=90°,∴⊥,∴·=0, 又=-=(2,2)-(-1,t)=(3,2-t), ∴(2,2)·(3,2-t)=6+2(2-t)=0, ∴t=5。 4. - 解析:选,为基底,则=-+, =-+, ∴·=(-+)·(-+)=-。 5. π 解析:设c=(x,y),则(a+b)·c=(-1,-2)·(x,y)=-x-2y=,∴x+2y=-,又|a|=|c|=,且a·c=x+2y=|a||c|·cos α,故cos α=-,α∈[0,π],α=π。 6. (3,0) 解析:设点P坐标为(x,0),则=(x-2,-2),=(x-4,-1),·=(x-2)(x-4)+(-2)×(-1)=x2-6x+10=(x-3)2+1,当x=3时,·有最小值1, ∴点P的坐标为(3,0)。 7. 解:∵(ka-b)⊥(a+2b), ∴(ka-b)·(a+2b)=0,ka2+(2k-1)a·b-2b2=0,k×52+(2k-1)×5×4×cos 60°-2×42=0, ∴k=,即k=时,向量ka-b与向量a+2b垂直。 8. 解:因为向量a+λb与a+b的夹角为锐角,所以(a+λb)·(a+b)=a2+(1+λ)a·b+λb2=12λ+5>0, 由此解得λ>-,若向量a+λb与a+b同向,则存在唯一的正数k,使得a+λb=k(a+b)成立,有k=λ=1, 要保证向量a+λb与a+b不同向,则必须λ≠1. 综上所述,当λ>-且λ≠1时,向量a+λb与a+b的夹角为锐角。 3 9. 解:∵a=(,-1),b=(,), ∴|a|==2, |b|==1, 又∵a·b=×+(-1)×=0,∴a⊥b, 由x⊥y得[a+(t2-3)b]·(-ka+tb)=0, 即-ka2+(t3-3t)b2+(t-kt2+3k)a·b=0, ∴-k|a|2+(t3-3t)|b|2=0. 将|a|=2,|b|=1代入上式,得-4k+t3-3t=0, 解得k=, ∴= (t2+4t-3)= (t+2)2-, 故当t=-2时,取得最小值,为-。 3查看更多