点、直线、平面之间的位置关系教案

点、直线、平面之间的位置关系教案

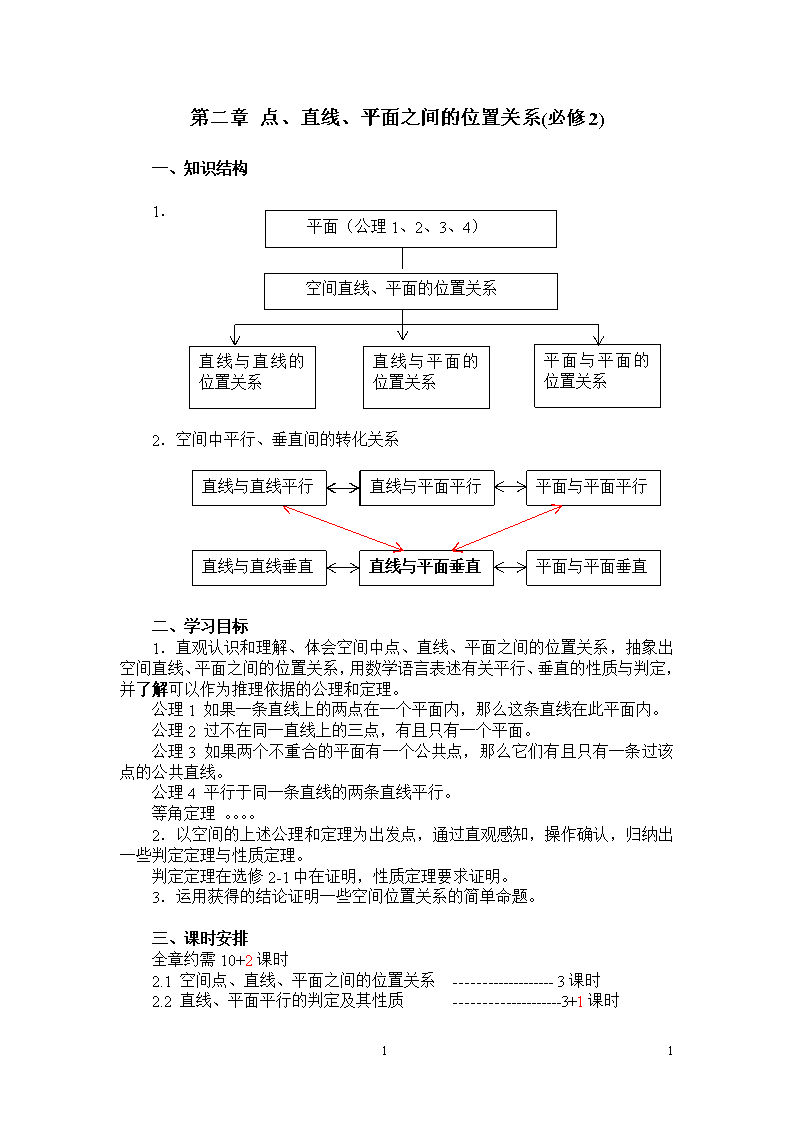
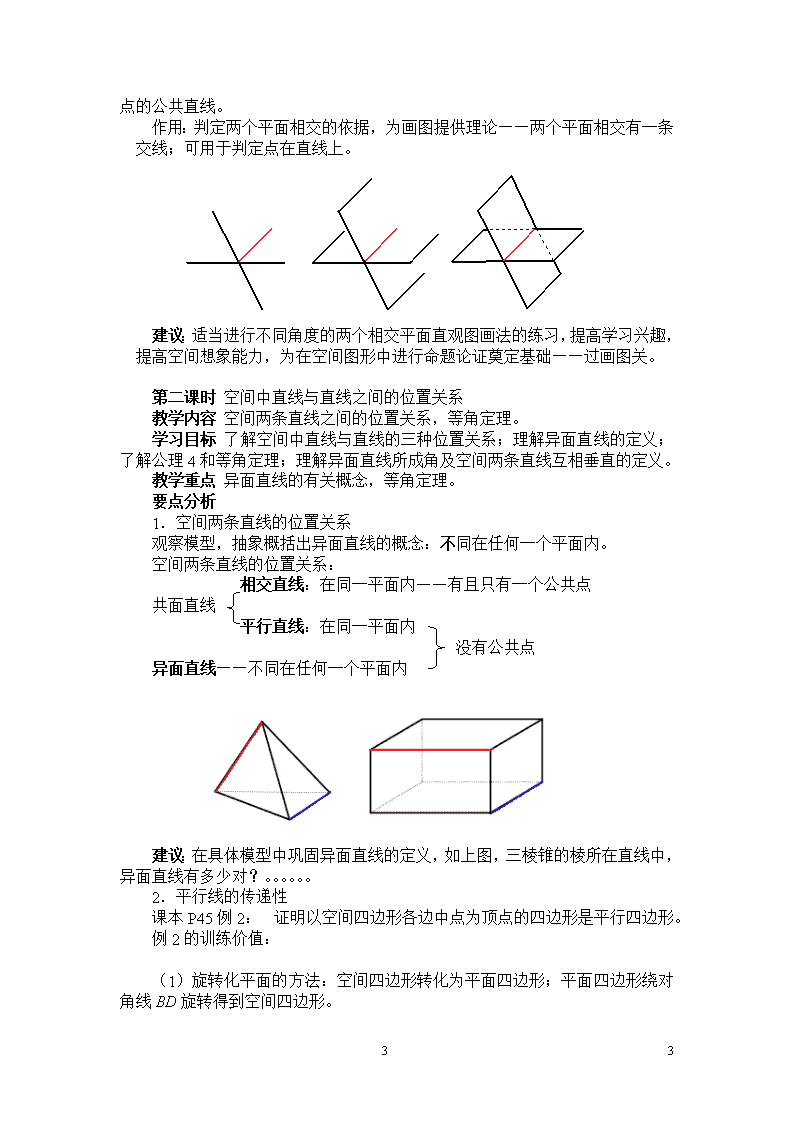
‎ ‎ 第二章 点、直线、平面之间的位置关系(必修2) ‎ ‎ ‎ 一、知识结构 平面（公理1、2、3、4）‎ 空间直线、平面的位置关系 直线与直线的位置关系 直线与平面的位置关系 平面与平面的位置关系 ‎1．‎ ‎ ‎ ‎2．空间中平行、垂直间的转化关系 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线垂直 直线与平面垂直 平面与平面垂直 直线与直线平行 直线与平面平行 二、学习目标 ‎1．直观认识和理解、体会空间中点、直线、平面之间的位置关系，抽象出空间直线、平面之间的位置关系，用数学语言表述有关平行、垂直的性质与判定，并了解可以作为推理依据的公理和定理。‎ 公理1 如果一条直线上的两点在一个平面内，那么这条直线在此平面内。‎ 公理2 过不在同一直线上的三点，有且只有一个平面。‎ 公理3 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。‎ 公理4 平行于同一条直线的两条直线平行。‎ 等角定理 。。。。‎ ‎2．以空间的上述公理和定理为出发点，通过直观感知，操作确认，归纳出一些判定定理与性质定理。‎ 判定定理在选修2-1中在证明，性质定理要求证明。‎ ‎3．运用获得的结论证明一些空间位置关系的简单命题。 ‎ 三、课时安排 全章约需10+2课时 ‎2.1 空间点、直线、平面之间的位置关系 ------------------- 3课时 ‎2.2 直线、平面平行的判定及其性质 --------------------3+1课时 13‎ 13‎ ‎ ‎ ‎2.3 直线、平面垂直的判定及其性质 --------------------3+1课时 小结 ----------------------------------1课时 四、教学建议 ‎2.1空间点、直线、平面之间的位置关系（3课时）‎ 第一课时 平面 教学内容 平面的概念；平面的画法和表示；平面的基本性质。‎ 学习目标 ‎ ‎1．了解平面的概念，理解平面的无限延展性。‎ ‎2．会正确地用图形和符号表示点、直线、平面及其它们之间的位置关系，初步掌握文字语言、图形语言、符号语言间的相互转化。‎ ‎3．了解作为以后推理依据的三个公理。‎ 教学重点 文字语言、图形语言、符号语言间的相互转化，三个公理的作用。 ‎ 要点分析 ‎1．三种语言间的联系 图形语言——考察对象第一次抽象的产物，形象、直观的语言。‎ 文字语言——对图像的描述、解释与讨论。‎ 符号语言——对文字语言的简化和再次抽象。‎ 在对空间图形的认识中，注意有序的建立三种数学语言间的联系，合理使用三种数学语言描述图形的性质，加深对图形性质的理解。‎ 课本按照图形语言——文字语言——符号语言——三种语言综合描述的顺序安排学习内容。‎ 注意：符号语言只是借用集合符号，读法仍用几何语言。‎ ‎2．两个重要模型 四面体、长方体作为图形语言的载体作用——典型性、简明性、直观性、概括性、趣味性。‎ 建议：要求学生能熟练画出四面体、长方体，利用这两个模型理解所学概念、定理，发展几何直观能力，提高空间想象力。 ‎ ‎3．平面的基本性质 公理1如果一条直线上的两点在一个平面内，那么这条直线在此平面内。‎ 作用：用直线的直刻划平面的平，是判断直线在平面内的依据。‎ 公理2 过不在同一直线上的三点，有且只有一个平面。‎ 作用：确定平面的依据。‎ 课本并没有给出常用的三个推论，只是在练习题中以判断题的形式涉及，建议学生将其作为重要结论使用，但不涉及推论字眼。‎ 公理 13‎ 13‎ ‎ ‎ ‎3 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。‎ 作用：判定两个平面相交的依据，为画图提供理论——两个平面相交有一条交线；可用于判定点在直线上。‎ 建议：适当进行不同角度的两个相交平面直观图画法的练习，提高学习兴趣，提高空间想象能力，为在空间图形中进行命题论证奠定基础——过画图关。‎ ‎ ‎ 第二课时 空间中直线与直线之间的位置关系 教学内容 空间两条直线之间的位置关系，等角定理。‎ 学习目标 了解空间中直线与直线的三种位置关系；理解异面直线的定义；了解公理4和等角定理；理解异面直线所成角及空间两条直线互相垂直的定义。‎ 教学重点 异面直线的有关概念，等角定理。 ‎ 要点分析 ‎1．空间两条直线的位置关系 观察模型，抽象概括出异面直线的概念：不同在任何一个平面内。‎ 空间两条直线的位置关系：‎ ‎ 相交直线：在同一平面内——有且只有一个公共点 共面直线 ‎ 平行直线：在同一平面内 ‎ ‎ 没有公共点 异面直线——不同在任何一个平面内 ‎ ‎ 建议：在具体模型中巩固异面直线的定义，如上图，三棱锥的棱所在直线中，异面直线有多少对？。。。。。。‎ ‎2．平行线的传递性 课本P45例2： 证明以空间四边形各边中点为顶点的四边形是平行四边形。‎ 例2的训练价值：‎ ‎（1）旋转化平面的方法：空间四边形转化为平面四边形；平面四边形绕对角线BD旋转得到空间四边形。‎ 13‎ 13‎ ‎ ‎ ‎（2）增加什么条件，四边形EFGH成为菱形、矩形、正方形？‎ ‎3．等角定理 通过对长方体模型的观察得到等角定理，鉴于长方体角度的特殊性，建议增加一点观察的难度，如下图2 。‎ 等角定理并不要求证明，只需观察确认，目的是为定义异面直线所成角提供理论支持。‎ ‎4．异面直线所成的角 利用平行投影感知异面直线所成的角：‎ 建议：P45探究作业难度较大，课上不作处理。‎ ‎ ‎ 第三课时 直线与平面、平面与平面之间的位置关系 教学内容 直线与平面的位置关系；平面与平面的位置关系。‎ 学习目标 ‎ ‎1．了解直线与平面的位置关系，理解直线在平面外的概念；了解空间两个平面的位置关系。‎ ‎ 2．通过对实物或模型的观察，直线、平面间位置关系的确认，再到熟知的长方体模型中位置关系的识别，使学生明确各种位置关系的本质特征，树立空间观念，提高画图和识图能力。‎ 教学重点 直线、平面间位置关系的确认。‎ 13‎ 13‎ ‎ ‎ 要点分析 ‎1．直线与平面的位置关系 直线在平面内—— —— —— —— —有无数个公共点 ‎ 有公共点 直线与平面相交——有且只有一个公共点 直线在平面外 ‎ 直线与平面平行—— —— —— —— —— 无公共点 建议：三种位置关系的图形表示，要求学生课上练习画法，并用符号语言表示，帮助学生纠正易犯的错误，如下图。‎ ‎2．两个平面的位置关系 两个平面平行——没有公共点。‎ 两个平面相交——有一条公共直线。‎ 建议：利用长方体模型，识别直线、平面间的各种位置关系。‎ ‎3．问题探究 ‎（1）已知平面，直线且，，则直线a与b具有怎样的位置关系？画出图形表示你的结论。‎ ‎（2）已知平面，直线且，，则直线a与b具有怎样的位置关系？画出图形表示你的结论。‎ ‎（3）P50 练习：如果三个平面两两相交，那么它们有多少条交线？画出图形表示你的结论。 ‎ 13‎ 13‎ ‎ ‎ ‎2.2 直线、平面平行的判定及其性质（3+1课时）‎ 第四课时 直线与平面平行的判定 教学内容 直线与平面平行的判定定理。‎ 学习目标 ‎ ‎1．理解直线与平面平行的判定定理，会利用定理在简单几何体中判定直线与平面是否平行。‎ ‎2．通过定理的应用，培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 操作确认直线与平面平行的判定方法，也是教学的难点。‎ 要点分析 ‎1．直线与平面平行的判定 定理： 。‎ 利用直线与直线的平行判断直线与平面的平行，即将线面平行问题转化为线线平行问题——转化思想方法的应用。‎ 直线与直线平行 直线与平面平行 ‎2．判定定理的应用 ‎（1）借助于长方体模型，熟悉巩固定理的条件，严格要求论证的叙述：三个条件缺一不可。‎ ‎（2）在（1）的基础上练习书面表述定理的应用。参看课本P55 例1。‎ 第五课时 平面与平面平行的判定 教学内容 平面与平面平行的判定定理。‎ 学习目标 ‎ ‎1．理解平面与平面平行的判定定理，会利用定理在简单几何体中判定平面与平面是否平行。‎ ‎2．通过定理的应用，培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 平面与平面平行判定方法的确认，也是教学的难点。‎ 要点分析 ‎1．平面与平面平行的判定定理 注意让学生体验转化思想的应用，转化关系为：‎ 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线平行 直线与平面平行 ‎2．定理的应用 建议：增加综合练习，提升学生的数学能力。‎ 例1 已知正方体ABCD-A1B1C1D1，E、F、G分别A1B1、A1D1、A1A的中点，求证：平面EFG//平面BC1D。‎ 13‎ 13‎ ‎ ‎ ‎ ‎ 例2 已知三棱锥P-ABCD中，E，F，G分别是边AB、PC、PB的中点，‎ 求证：平面PAD// 平面EFG。 ‎ ‎3．类比思维训练 类比平面几何的一些结论，可以得到空间图形的一些重要性质，从素质教育的角度出发，建议进行必要的类比思维训练。‎ 例 平面几何中有如下结论：如图，线段AB、CD相交于点O且互相平分，则直线 AC// BD。‎ ‎ ‎ ‎ ‎ ‎ ‎ 类比上述结论，在空间，你能得到什么结论？ ‎ 第六课时 直线与平面平行的性质 教学内容 直线与平面平行的性质定理。‎ 学习目标 ‎ ‎1．掌握直线与平面平行的性质定理，较为灵活的运用所学定理在几何体中证明简单的命题。‎ ‎2．培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 操作确认——逻辑证明。‎ 要点分析 ‎1．直线与平面平行的性质定理 注意空间中平行关系的转化：‎ 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线平行 直线与平面平行 ‎2．定理的应用 例1 如图，已知平面，直线，求证：。‎ 13‎ 13‎ ‎ ‎ ‎ ‎ ‎3．类比思维训练 ‎ 例2 平面几何中有如下结论：平行线间的平行线段相等。‎ ‎ ‎ 类比上述结论，由直线 //平面，你能得到什么结论？能把你的结论再推广吗？‎ 第七课时 平面与平面平行的性质 教学内容 平面与平面平行的性质定理。‎ 学习目标 ‎ ‎1．掌握平面与平面平行的性质定理，能较为灵活的运用所学定理在几何体中证明简单的命题。‎ ‎2．培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 性质定理的证明及其应用 要点分析 ‎1．平面与平面平行的性质定理 ‎ 空间中平行关系的转化——知识结构：‎ 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线平行 直线与平面平行 ‎2．类比思维训练 例 平面几何中有如下结论：如图，平行线截直线所得线段成比例。‎ 类比上述结论，在空间，你能得到什么结论？试给出证明。‎ ‎2.3 直线、平面垂直的判定及其性质（3+1课时）‎ 13‎ 13‎ ‎ ‎ 第八课时 直线与平面垂直的判定 教学内容 直线与平面垂直的定义、判定；直线和平面所成的角。‎ 学习目标 ‎ ‎1．理解直线与平面垂直的定义；掌握直线与平面垂直的判定定理，会用定义和定理判定几何图形中直线与平面的垂直关系；理解直线与平面所成角的定义，会在简单空间图形中求直线和平面所成的角。‎ ‎2．通过直观感知、操作确认、定理应用等教学活动，培养学生空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 直线与平面垂直的判定定理及其应用。‎ 要点分析 ‎1．直线与平面垂直的判定 通过直观感知、操作确认，得到直线与平面垂直的判定方法。‎ ‎ 将三角形纸片沿AD折起，折线BD、CD确定一个平面，折痕AD与平面BCD垂直吗？ 如何翻折才能使AD垂直平面BCD垂直？‎ 直线与平面垂直的判定定理：‎ ‎。定理中三个条件缺一不可。‎ 建议：（1）通过反例引起学生对条件 的必要性认识。‎ ‎（2）利用长方体图形对定理进行巩固练习，提高学生论证的严谨性。‎ ‎2．在两个重要模型中强化判定定理 ‎（1）正方体ABCD- A1B1C1D1中，对角线A1C垂直平面AB1D1和BC1D。‎ ‎（2）正三棱锥P-ABC中，相对的棱互相垂直。‎ ‎ ‎ 13‎ 13‎ ‎ ‎ ‎2．知识结构 ‎ ‎ 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线垂直 直线与平面垂直 ‎3．直线与平面所成的角 建议：在两个重要模型中进行强化练习。 ‎ 例 如图，三棱锥P-ABC中，平面。求：‎ ‎（1）PA，PB，PC与平面PBC所成的角； ‎ ‎（2）AC，AB，AP与平面PBC所成的角。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 第九课时 平面与平面垂直的判定 教学内容 二面角；平面与平面垂直的定义、判定。‎ 学习目标 ‎ ‎1．理解二面角的有关概念；掌握平面与平面垂直的判定定理。‎ ‎2．培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 平面与平面垂直的判定定理的确认。‎ 要点分析 ‎1．二面角 ‎（1）二面角画法练习——不同方向的二面角的画法 ‎（2）二面角求法练习 课本没有求二面角大小的题例，建议在具体简单图形中巩固有关概念。‎ 13‎ 13‎ ‎ ‎ ‎2．知识结构 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线垂直 直线与平面垂直 平面与平面垂直 直线与直线平行 直线与平面平行 ‎3．问题探究 ‎ ‎（1）如图，三棱锥P-ABC中，平面，问：图中有几对面互相垂直？ 并给出证明。‎ ‎（2）如图，四棱锥P-ABCD中，是矩形，问：图中有几对面互相垂直？ 并给出证明。‎ 第十课时 直线与平面垂直的性质 教学内容 直线与平面垂直的性质。‎ 学习目标 ‎ ‎1．掌握直线与平面垂直的性质定理。‎ ‎2．培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 直线与平面垂直的性质定理的应用。难点是定理的证明。‎ 要点分析 ‎1．知识结构 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线垂直 直线与平面垂直 平面与平面垂直 直线与直线平行 直线与平面平行 ‎ ‎ ‎2．性质定理的证明 定理的证明引用了反证法，这是教学的难点。‎ 13‎ 13‎ ‎ ‎ ‎3．定理的应用 通过定理的应用，体验转化思想在几何中的具体运用，提高逻辑论证能力。 ‎ 例 如图，四棱锥P-ABCD中，是矩形，M是PC中点，证明平面。‎ ‎4．问题探究 下述两个位置关系之间能进行相互转化吗？ ‎ 直线与平面垂直 平面与平面平行 第十一课时 平面与平面垂直的性质 教学内容 平面与平面垂直的性质。‎ 学习目标 ‎ ‎1．平面与平面垂直的性质定理。‎ ‎2．培养空间想象能力和逻辑论证能力，体验转化思想在几何中的运用。‎ 教学重点 平面与平面垂直的性质定理的应用。难点是定理的证明。‎ 要点分析 ‎1．知识结构 直线与直线平行 直线与平面平行 平面与平面平行 直线与直线垂直 直线与平面垂直 平面与平面垂直 直线与直线平行 直线与平面平行 ‎2．定理的证明 直观感知——提出猜想——逻辑证明。‎ 定理的证明用到同一法，难度较大，是本节课的难点。‎ ‎3．线面位置关系的判定练习 建议：增加一定量的选择题、判断题巩固所学定理。‎ 例 （2007辽宁，理7题）若是两条不同的直线，‎ 13‎ 13‎ ‎ ‎ 是三个不同的平面，则下列命题中的真命题是（ ）‎ A．若，则 ‎ B．若，，则 C．若，，则 ‎ D．若，，则 ‎4．定理的应用 如图，三棱锥P-ABC中，平面。求：‎ ‎（1）PC与平面PAB所成的角； ‎ ‎（2）PB与平面PAC所成的角。‎ ‎ ‎ ‎ ‎ 第十二课时 小结 13‎ 13‎