- 2021-06-16 发布 |
- 37.5 KB |
- 124页

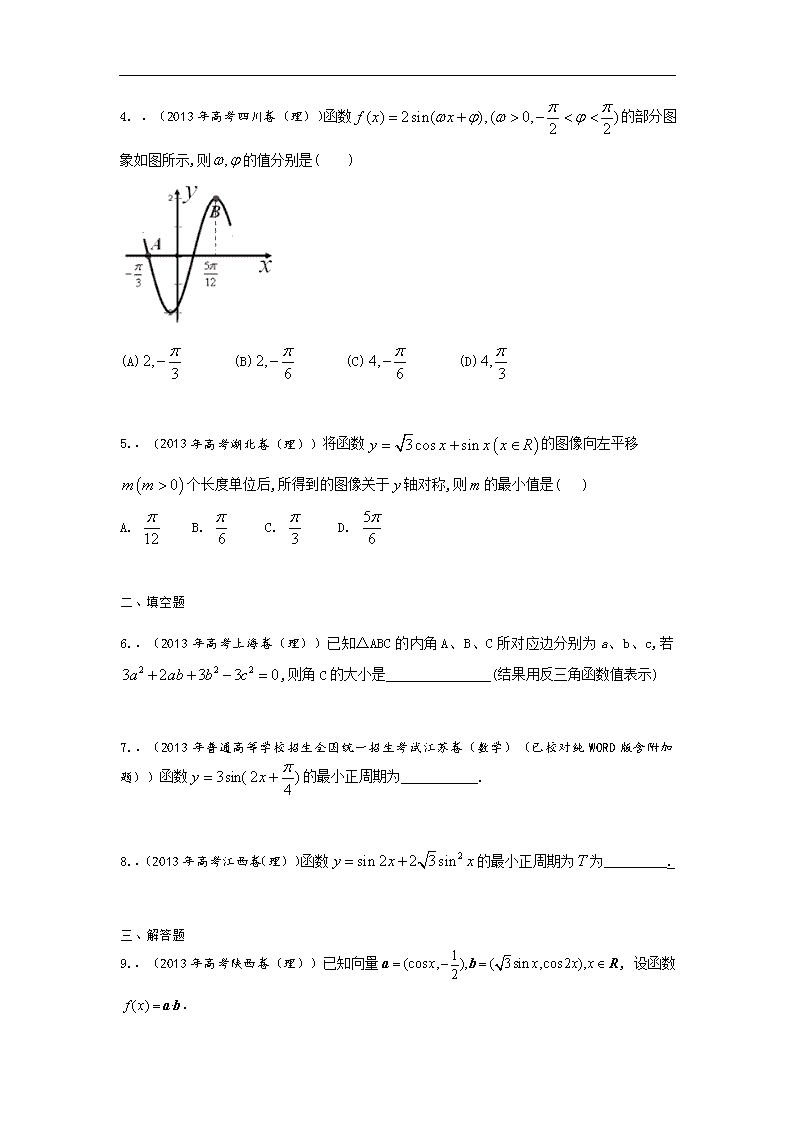

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【高考一模·北京西城】北京市西城区2010年高三一模数学理科试题(含答案)
【数学】2014版《6年高考4年模拟》 第四章 三角函数及三角恒等变换 第二节 三角函数的图象和性质及三角恒等变换 第一部分 六年高考荟萃 2013年高考题 一、选择题 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为 (A) (B) (C)0 (D) .(2013年普通高等学校招生统一考试大纲版数学(理)WORD版含答案(已校对))已知函数,下列结论中错误的是 (A)的图像关于中心对称 (B)的图像关于直线对称 (C)的最大值为 (D)既奇函数,又是周期函数 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))函数的图象大致为 .(2013年高考四川卷(理))函数的部分图象如图所示,则的值分别是( ) (A) (B) (C) (D) .(2013年高考湖北卷(理))将函数的图像向左平移个长度单位后,所得到的图像关于轴对称,则的最小值是( ) A. B. C. D. 二、填空题 .(2013年高考上海卷(理))已知△ABC的内角A、B、C所对应边分别为a、b、c,若,则角C的大小是_______________(结果用反三角函数值表示) .(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD版含附加题))函数的最小正周期为___________. .(2013年高考江西卷(理))函数的最小正周期为为_________. 三、解答题 .(2013年高考陕西卷(理))已知向量, 设函数. (Ⅰ) 求f (x)的最小正周期. (Ⅱ) 求f (x) 在上的最大值和最小值. .(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))已知函数. (Ⅰ) 求f(x)的最小正周期; (Ⅱ) 求f(x)在区间上的最大值和最小值. .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD版))设向量 (I)若 (II)设函数 .(2013年高考上海卷(理))(6分+8分)已知函数,其中常数; (1)若在上单调递增,求的取值范围; (2)令,将函数的图像向左平移个单位,再向上平移1个单位,得到函数的图像,区间(且)满足:在上至少含有30个零点,在所有满足上述条件的中,求的最小值. .(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))已知函数的最小正周期为. (Ⅰ)求的值; (Ⅱ)讨论在区间上的单调性. .(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD版))已知函数的周期为,图像的一个对称中心为,将函数图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移个单位长度后得到函数的图像. (1)求函数与的解析式; (2)是否存在,使得按照某种顺序成等差数列?若存在,请确定的个数;若不存在,说明理由. (3)求实数与正整数,使得在内恰有2013个零点. .(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD版含附加题))本小题满分14分.已知,. (1)若,求证:;(2)设,若,求的值. .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD版))已知函数,. (Ⅰ) 求的值; (Ⅱ) 若,,求. .(2013年高考湖南卷(理))已知函数. (I)若是第一象限角,且.求的值; (II)求使成立的x的取值集合. .(2013年上海市春季高考数学试卷(含答案))本题共有2个小题,第一小题满分4分,第二小题满分9分. 在平面直角坐标系中,点在轴正半轴上,点在轴上,其横坐标为,且 是首项为1、公比为2的等比数列,记,. (1)若,求点的坐标; (2)若点的坐标为,求的最大值及相应的值. P2 0 x y A P1 P3 P4 2012年高考题 一、选择题 1.【2012高考重庆理5】设是方程的两个根,则的值为 (A)-3 (B)-1 (C)1 (D)3 2.【2012高考浙江理4】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是 3.【2012高考新课标理9】已知,函数在上单调递减.则的取值范围是( ) 4.【2012高考四川理4】如图,正方形的边长为,延长至,使,连接、则( ) A、 B、 C、 D、 5.【2012高考陕西理9】在中,角所对边长分别为,若,则的最小值为( ) A. B. C. D. 6.【2012高考山东理7】若,,则 (A) (B) (C) (D) 7.【2012高考辽宁理7】已知,(0,π),则= (A) 1 (B) (C) (D) 1 8.【2012高考江西理4】若tan+ =4,则sin2= A. B. C. D. 9.【2012高考湖南理6】函数f(x)=sinx-cos(x+)的值域为 A. [ -2 ,2] B.[-,] C.[-1,1 ] D.[- , ] 10.【2012高考上海理16】在中,若,则的形状是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 11.【2012高考天津理2】设则“”是“为偶函数”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分与不必要条件 12.【2012高考天津理6】在中,内角A,B,C所对的边分别是,已知8b=5c,C=2B,则cosC= (A) (B) (C) (D) 13.【2012高考全国卷理7】已知α为第二象限角,,则cos2α= (A) (B) (C) (D) 二、填空题 14.【2012高考湖南理15】函数f(x)=sin ()的导函数的部分图像如图4所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点. (1)若,点P的坐标为(0,),则 ; (2)若在曲线段与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 . 15.【2012高考湖北理11】设△的内角,,所对的边分别为,,. 若,则角 . 16.【2012高考北京理11】在△ABC中,若=2,b+c=7,cosB=,则b=_______。 17.【2012高考安徽理15】设的内角所对的边为;则下列命题正确的是 ①若;则 ②若;则 ③若;则 ④若;则 ⑤若;则 18.【2012高考福建理13】已知△ABC得三边长成公比为的等比数列,则其最大角的余弦值为_________. 19.【2012高考重庆理13】设的内角的对边分别为,且,,则 20.【2012高考上海理4】若是直线的一个法向量,则的倾斜角的大小 为 (结果用反三角函数值表示)。 21.【2012高考全国卷理14】当函数取得最大值时,x=___________. 22.【2012高考江苏11】(5分)设为锐角,若,则的值为 ▲ . 三、解答题 23.【2012高考新课标理17】(本小题满分12分) 已知分别为三个内角的对边, (1)求 (2)若,的面积为;求. 24.【2012高考湖北理17】(本小题满分12分) 已知向量,,设函数的图象关于直线对称,其中,为常数,且. (Ⅰ)求函数的最小正周期; (Ⅱ)若的图象经过点,求函数在区间上的取值范围. 25.【2012高考安徽理16】)(本小题满分12分) 设函数。 (I)求函数的最小正周期; (II)设函数对任意,有,且当时, ,求函数在上的解析式。 26.【2012高考四川理18】(本小题满分12分) 函数在一个周期内的图象如图所示,为图象的最高点,、为图象与轴的交点,且为正三角形。 (Ⅰ)求的值及函数的值域; (Ⅱ)若,且,求的值。 27.【2012高考陕西理16】(本小题满分12分) 函数()的最大值为3, 其图像相邻两条对称轴之间的距离为, (1)求函数的解析式; (2)设,则,求的值。 28.【2012高考广东理16】(本小题满分12分) 已知函数,(其中ω>0,x∈R)的最小正周期为10π. (1)求ω的值; (2)设,,,求cos(α+β)的值. 29.【2012高考山东理17】(本小题满分12分) 已知向量,函数的最大值为6. (Ⅰ)求; (Ⅱ)将函数的图象向左平移个单位,再将所得图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数的图象.求在上的值域. 30.【2012高考北京理15】(本小题共13分)已知函数。 (1)求的定义域及最小正周期; (2)求的单调递减区间。 31.【2012高考重庆理18】(本小题满分13分(Ⅰ)小问8分(Ⅱ)小问5分) 设,其中 (Ⅰ)求函数 的值域 (Ⅱ)若在区间上为增函数,求 的最大值. 32.【2012高考浙江理18】(本小题满分14分)在ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=,sinB=cosC. (Ⅰ)求tanC的值; (Ⅱ)若a=,求ABC的面积. 33.【2012高考辽宁理17】(本小题满分12分) 在中,角A、B、C的对边分别为a,b,c。角A,B,C成等差数列。 (Ⅰ)求的值; (Ⅱ)边a,b,c成等比数列,求的值。 34.【2012高考江西理17】(本小题满分12分) 在△ABC中,角A,B,C的对边分别为a,b,c。已知 (1)求证: (2)若,求△ABC的面积。 35.【2012高考全国卷理17】(本小题满分10分) 三角形ABC的内角A、B、C的对边分别为a、b、c,已知cos(A-C)+cosB=1,a=2c,求c. 36.【2012高考天津理15】(本小题满分13分) 已知函数 (Ⅰ)求函数的最小正周期; (Ⅱ)求函数在区间上的最大值和最小值. 37.【2012高考江苏15】(14分)在中,已知. (1)求证:; (2)若求A的值. 2011年高考题 一、选择题 1.(山东理6)若函数 (ω>0)在区间上单调递增,在区间上单调递减,则ω= A.3 B.2 C. D. 2.(山东理9)函数的图象大致是 3.(全国大纲理5)设函数,将的图像向右平移个单位长度后,所得的图像与原图像重合,则的最小值等于 A. B. C. D. 4.(湖北理3)已知函数,若,则x的取值范围为 A. B. C. D. 5.(全国新课标理11)设函数的最小正周期为,且则 (A)在单调递减 (B)在单调递减 (C)在单调递增 (D)在单调递增 6.(安徽理9)已知函数,其中为实数,若对恒成立,且 ,则的单调递增区间是 (A) (B) (C) (D) 二、填空题 7.(上海理8)函数的最大值为 。 8.(辽宁理16)已知函数=Atan(x+)(),y=的部分图像如下图,则 . 三、解答题 9.(江苏9)函数是常数,的部分图象如图所示,则f(0)= 10(北京理15) 已知函数。 (Ⅰ)求的最小正周期: (Ⅱ)求在区间上的最大值和最小值。 11.(福建理16) 已知等比数列{an}的公比q=3,前3项和S3=。 (I)求数列{an}的通项公式; (II)若函数在处取得最大值,且最大值为a3,求函数f(x)的解析式。 12.(广东理16) 已知函数 (1)求的值; (2)设求的值. 13.(湖北理16) 设的内角A、B、C、所对的边分别为a、b、c,已知 (Ⅰ)求的周长 (Ⅱ)求的值 14.(四川理17) 已知函数 (1)求的最小正周期和最小值; (2)已知,求证: 15.(天津理15) 已知函数 (Ⅰ)求的定义域与最小正周期; (II)设,若求的大小. 16.(重庆理16) 设,满足,求函数在上的最大值和最小值. 2010年高考题 一、选择题 1.(2010全国卷2理)(7)为了得到函数的图像,只需把函数的图像 (A)向左平移个长度单位 (B)向右平移个长度单位 (C)向左平移个长度单位 (D)向右平移个长度单位 2.(2010陕西文)3.函数f (x)=2sinxcosx是 (A)最小正周期为2π的奇函数 (B)最小正周期为2π的偶函数 (C)最小正周期为π的奇函数 (D)最小正周期为π的偶函数 3.(2010辽宁文)(6)设,函数的图像向右平移个单位后与原图像重合,则的最小值是 (A) (B) (C) (D) 3 4.(2010辽宁理)(5)设>0,函数y=sin(x+)+2的图像向右平移个单位后与原图像重合,则的最小值是 (A) (B) (C) (D)3 5.(2010重庆文)(6)下列函数中,周期为,且在上为减函数的是 (A) (B) (C) (D) 6.(2010重庆理) (6)已知函数的部分图象如题(6)图所示,则 A. =1 = B. =1 =- C. =2 = D. =2 = - 7.(2010山东文)(10)观察,,,由归纳推理可得:若定义在上的函数满足,记为的导函数,则= (A) (B) (C) (D) 8.(2010四川理)(6)将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 (A) (B) (C) (D) 9.(2010天津文)(8) 为了得到这个函数的图象,只要将的图象上所有的点 (A)向左平移 个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变 (B) 向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 (C) 向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变 (D) 向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 10.(2010福建文) 11.(2010四川文)(7)将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 (A) (B) (C) (D) 12.(2010湖北文)2.函数f(x)= 的最小正周期为 A. B.x C.2 D.4 13.(2010福建理)1.的值等于( ) A. B. C. D. 二、填空题 1.(2010浙江理)(11)函数的最小正周期是__________________ . 2.(2010浙江文)(12)函数的最小正周期是 。 3.(2010福建文)16.观察下列等式: ① cos2a=2-1; ② cos4a=8- 8+ 1; ③ cos6a=32- 48+ 18- 1; ④ cos8a=128- 256+ 160- 32+ 1; ⑤ cos10a= m- 1280+ 1120+ n+ p- 1. 可以推测,m – n + p = . 4.(2010山东理) 5.(2010福建理)14.已知函数和的图象的对称轴完全相同。若,则的取值范围是 。 6.(2010江苏卷)10、定义在区间上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为____________。 三、解答题 1.(2010湖南文)16. (本小题满分12分) 已知函数 (I)求函数的最小正周期。 (II) 求函数的最大值及取最大值时x的集合。 2.(2010浙江理)(18)(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c,已知 (I)求sinC的值; (Ⅱ)当a=2, 2sinA=sinC时,求b及c的长. 3.(2010江西理)17.(本小题满分12分) 已知函数。 (1) 当m=0时,求在区间上的取值范围; (2) 当时,,求m的值。 4.(2010浙江文)(18)(本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足。 (Ⅰ)求角C的大小; (Ⅱ)求的最大值。 5.(2010北京文)(15)(本小题共13分) 已知函数 (Ⅰ)求的值; (Ⅱ)求的最大值和最小值 6.(2010北京理)(15)(本小题共13分) 已知函数。 (Ⅰ)求的值; (Ⅱ)求的最大值和最小值。 7.(2010广东理)16、(本小题满分14分) 已知函数在时取得最大值4. (1) 求的最小正周期; (2) 求的解析式; (3) 若(α +)=,求sinα. 8.(2010广东文) 9.(2010湖北文)16.(本小题满分12分) 已经函数 (Ⅰ)函数的图象可由函数的图象经过怎样变化得出? (Ⅱ)求函数的最小值,并求使用取得最小值的的集合。 10.(2010湖南理)16.(本小题满分12分) 已知函数. (Ⅰ)求函数的最大值; (II)求函数的零点的集合。 2009年高考题 一、选择题 1.(2009年广东卷文)函数是 A.最小正周期为的奇函数 B. 最小正周期为的偶函数 C. 最小正周期为的奇函数 D. 最小正周期为的偶函数 2.(2009全国卷Ⅰ理)如果函数的图像关于点中心对称,那么的最小值为( ) A . B. C. D. 3.(2009全国卷Ⅰ理)若,则函数的最大值为 。 4..(2009浙江理)已知是实数,则函数的图象不可能是 ( ) 5..(2009浙江文)已知是实数,则函数的图象不可能是( ) 6.(2009山东卷理)将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ). A. B. C. D. 7.(2009山东卷文)将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ). A. B. C. D. 8.(2009安徽卷理)已知函数,的图像与直线的两个相邻交点的距离等于,则的单调递增区间是 A. B. C. D. 9..(2009安徽卷文)设函数,其中,则导数的取值范围是 A. B. C. D. 10.(2009江西卷文)函数的最小正周期为 A. B. C. D. 11.(2009江西卷理)若函数,,则的最大值为 A.1 B. C. D. 12.(2009湖北卷理)函数的图象按向量平移到,的函数解析式为当为奇函数时,向量可以等于 13.(2009全国卷Ⅱ理)若将函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为 A. B. C. D. 14..(2009福建卷理)函数最小值是 ( ) A.-1 B. C. D.1 15.(2009辽宁卷理)已知函数=Acos()的图象如图所示,,则=( ) A. B. C.- D. 16.(2009全国卷Ⅰ文)如果函数的图像关于点中心对称,那么的最小值为 A. B. C. D. 17.(2009湖北卷文)函数的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于 A. B. C. D. 18.(2009湖南卷理)将函数y=sinx的图象向左平移0 <2的单位后,得到函数y=sin的图象,则等于 (D) A. B. C. D. 19.(2009天津卷理)已知函数的最小正周期为,为了得到函数的图象,只要将的图象 A 向左平移个单位长度 B 向右平移个单位长度 C 向左平移个单位长度 D 向右平移个单位长度 二、填空题 20.(2009江苏卷)函数(为常数,)在闭区间上的图象如图所示,则= . 21(2009宁夏海南卷理)已知函数y=sin(x+)(>0, -<)的图像如图所示,则 =________________ 22.(2009宁夏海南卷文)已知函数的图像如图所示,则 。 23.(2009湖南卷理)若x∈(0, )则2tanx+tan(-x)的最小值为 24.(2009年上海卷理)函数的最小值是_____________________ . 25.(2009年上海卷理)当,不等式成立,则实数的取值范围是_______________. 26.(2009年上海卷理)已知函数.项数为27的等差数列满足,且公差.若,则当=____________是,. 27.(2009上海卷文)函数的最小值是 。 28.(2009辽宁卷文)已知函数的图象如图所示, 则 = 三、解答题 29.(2009全国卷Ⅰ理)在中,内角A、B、C的对边长分别为、、,已知,且 求b 30.(2009北京文)(本小题共12分)已知函数. (Ⅰ)求的最小正周期; (Ⅱ)求在区间上的最大值和最小值. 31.(2009北京理)(本小题共13分) 在中,角的对边分别为,。 (Ⅰ)求的值; (Ⅱ)求的面积. 32.(2009江苏卷) 设向量 (1)若与垂直,求的值; (2)求的最大值; (3)若,求证:∥. 33.(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+)+sinx. (1) 求函数f(x)的最大值和最小正周期. (2) 设A,B,C为ABC的三个内角,若cosB=,,且C为锐角,求sinA. 34.(2009山东卷文)(本小题满分12分)设函数f(x)=2在处取最小值. (1) 求.的值; (2) 在ABC中,分别是角A,B,C的对边,已知,求角C.. 35.(2009全国卷Ⅱ文)(本小题满分12分)设△ABC的内角A、B、C的对边长分别为a、b、c,,,求B. 解析:本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB=(负值舍掉),从而求出B=。 36.(2009江西卷文)(本小题满分12分) 在△中,所对的边分别为,,. (1)求; (2)若,求,,. 37.(2009江西卷理)△中,所对的边分别为,,. (1)求; (2)若,求. 38.(2009全国卷Ⅱ理)设的内角、、的对边长分别为、、,,,求。 39.(2009陕西卷理)(本小题满分12分) 已知函数(其中)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为. (Ⅰ)求的解析式;(Ⅱ)当,求的值域. 40.(2009湖北卷文) 在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 (Ⅰ)确定角C的大小: (Ⅱ)若c=,且△ABC的面积为,求a+b的值。 41.(2009湖南卷理)在,已知,求角A,B,C的大小. 42.(2009福建卷文).c.o.m 已知函数其中, (I)若求的值; (Ⅱ)在(I)的条件下,若函数的图像的相邻两条对称轴之间的距离等于,求函数的解析式;并求最小正实数,使得函数的图像象左平移个单位所对应的函数是偶函数。 43.(2009重庆卷理)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.) 设函数. (Ⅰ)求的最小正周期. (Ⅱ)若函数与的图像关于直线对称,求当时的最大值. 44.(2009重庆卷文)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.) 设函数的最小正周期为. (Ⅰ)求的最小正周期. (Ⅱ)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间. 45.(2009上海卷文)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分 . 已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量, , . (1) 若//,求证:ΔABC为等腰三角形; (2) 若⊥,边长c = 2,角C = ,求ΔABC的面积 . w 2008年高考题 一、选择题 1.(2008山东)函数的图象是 ( ) y x 1 1 O 2.(海南、宁夏理科卷)已知函数)在区间的图像如下:那么=( ) A.1 B.2 C. D. 3、(2008广东)已知函数,则是( ) A、最小正周期为的奇函数 B、最小正周期为的奇函数 C、最小正周期为的偶函数 D、最小正周期为的偶函数 4.(2008海南、宁夏文科卷)函数的最小值和最大值分别为( ) A. -3,1 B. -2,2 C. -3, D. -2, 5.(2007福建)已知函数的最小正周期为,则该函数的图象( ) A.关于点对称 B.关于直线对称 C.关于点对称 D.关于直线对称 6.(2007广东)若函数,则是( ) A.最小正周期为的奇函数 B.最小正周期为的奇函数 C.最小正周期为的偶函数 D.最小正周期为的偶函数 7.(2007海南、宁夏)函数在区间的简图是( ) 8.(2007浙江)若函数,(其中,)的最小正周期是,且,则( ) A. B. C. D. 二、填空题 12.(2008江苏卷)的最小正周期为,其中,则 13.(广东理科卷)已知函数,,则的最小正周期是 . 14.(2007安徽)函数的图象为,如下结论中正确的是__________(写出所有正确结论的编号). ①图象关于直线对称; ②图象关于点对称; ③函数在区间内是增函数; ④由的图角向右平移个单位长度可以得到图象 15.(2007四川)下面有五个命题: ①函数y=sin4x-cos4x的最小正周期是. ②终边在y轴上的角的集合是{a|a=}. ③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点. ④把函数 ⑤函数 其中真命题的序号是 三、解答题 16.(2008山东)已知函数f(x)=为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 (Ⅰ)求f()的值; (Ⅱ)将函数y=f(x)的图象向右平移个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间. 17.(2008广东)已知函数,的最大值是1,其图像经过点. (1)求的解析式; (2)已知,且,,求的值. 18.(2007湖北)已知函数,. (I)设是函数图象的一条对称轴,求的值. (II)求函数的单调递增区间. 第二部分 四年联考汇编 2013-2014年联考题 一、选择题 1、(绵阳市南山中学2014届高三上学期12月月考)要得到函数的图象,只需将函数的图象上所有点的( ) A. 横坐标缩短到原来的(纵坐标不变),所得图象再向左平移个单位长度. B. 横坐标缩短到原来的(纵坐标不变),所得图象再向右平移个单位长度. C. 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移个单位长度. D. 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移个单位长度. 2、(雅安中学2014届高三上学期12月月考)已知,则的值是 A. 3 B . —3 C. 2 D. -2 3、(成都七中2014届高三上期中考试)已知,则=( ) A. B. C. D. 4、(绵阳市高中2014届高三11月第一次诊断性考试)已知函数其中k>0,若当自变量x在任何两个整数间(包括整数本身)变化 时,至少含有2个周期,则最小的正整数k为 A、50 B、51 C、12 D、13 5、(成都石室中学2014届高三上学期期中)函数的最小正周期是( ) A. B. C. 2π D. 4π 6、(成都市2014届高三上学期摸底)若的值为 A. -1 B. C.l D.2 8、(泸州市2014届高三第一次教学质量诊断)将函数的图象向右平移个单位长度后得到函数的图象,若、的图象都经过点,则的值可以是 A. B. C. D. 9、(乐山市第一中学2014届高三10月月考)已知函数( ) A、 B、 C、 D、 10、(德阳中学2014届高三“零诊”考试) 把函数的图象向右平移个单位,再把所得函数图象上各点的横坐标缩短 为原来的,所得的函数解析式为( ) A. B. C. D. 11、(乐山市第一中学2014届高三10月月考)为了得到函数的图像,只需把函数的图像上所有的点( ) (A)向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变) (B)向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变) (C)向左平移个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) (D)向右平移个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) 12、(泸州市2014届高三第一次教学质量诊断)函数的图象大致为 A. B. C. D. 13、(绵阳市高中2014届高三11月第一次诊断性考试)下列不等式中,正确的是 A、sin1°>cos1 B、sin1>cos1° C、sin1<sin2 D、sin2<sin3 14、(什邡中学高中2014届高三上学期第二次月考)将函数图象上所有点的横坐标伸长到原来的2倍,再向右平移个单位长度,得到函数的图象,则图象的解析式是( ) A. B. C. D. 15、(资阳市2014届高三上学期第一次诊断性考试) 中,若,则 (A) (B) (C) (D) 16、(资阳市2014届高三上学期第一次诊断性考试)若把函数()的图象向左平移个单位后与函数的图象重合,则的值可能是 (A) (B) (C) (D) 17、(雅安中学2014届高三上学期12月月考)在ΔABC中,角A,B,C所对的边的长分别为,若,则 ΔABC的形状是 A.锐角三角 B.直角三角形 C.钝角三角形 D.正三角形 18、(绵阳市高中2014届高三11月第一次诊断性考试)已知都是锐角,且,则tan为 A、2 B、- C、-或2 D、或-2 二、填空题 1、(成都七中2014届高三上期中考试)已知,,则= . 2、(成都七中2014届高三上期中考试)ΔABC中,B=120º,AC=3,AB=,则ΔABC的面积为 . 3、(成都七中2014届高三上期中考试)在平面直角坐标系中,已知角的顶点在坐标原点,始边在轴的非负半轴上,终边经过点,则 4、(德阳中学2014届高三“零诊”考试)已知,则 5、(乐山市第一中学2014届高三10月月考) 函数是常数,的部分图象如图所示,则 6、(乐山市第一中学2014届高三10月月考)设为锐角,若,则的值为 . 7、(什邡中学高中2014届高三上学期第二次月考)设θ为第二象限角,若tan(θ+)=,则sinθ+cosθ= . 8、(资阳市2014届高三上学期第一次诊断性考试)在平面直角坐标系中,角α的顶点与原点重合,始边与x轴的非负半轴重合,若角α终边经过点,则___________. 三、解答题, 1、(绵阳市南山中学2014届高三上学期12月月考) 已知函数,. (I)若,求函数的最大值和最小值,并写出相应的x的值; (II)设的内角、、的对边分别为、、,满足,且,求、的值. 2、(成都七中2014届高三上期中考试) ΔABC中,,. (1)求证:; (2)若a、b、c分别是角A、B、C的对边,,求c和ΔABC的面积. 3、(成都高新区2014届高三10月统一检测) 已知函数,. (Ⅰ)求函数的最小值和最小正周期; (Ⅱ)设的内角、、的对边分别为、、,满足,且,求、的值. 4、(成都石室中学2014届高三上学期期中) 已知中,角的对边分别为,且有。 (1)求角的大小; (2)设向量,且,求的值。 5、(树德中学高2014届高三上学期期中) 已知函数(其中)的图象如图所示. (1) 求函数的解析式; (2) 设函数,且, 求的单调区间. 6、(成都外国语学校2014届高三11月月考) 已知函数.(1)求的值; (2)若对于任意的,都有,求实数的取值范围. 7、(达州市普通高中2014届高三第一次诊断检测) 如图所示,图象为函数 的部分图象如图所示 (1) 求的解析式. (2) 已知且求的值。 8、(德阳中学2014届高三“零诊”考试) 已知函数, 且函数的最小正周期为(1)求的值和函数的单调增区间;(2)在中,角A、B、C所对的边分别是、、,又,,的面积等于,求边长的值. 9、(乐山市第一中学2014届高三10月月考) 已知函数()的最小正周期为. (Ⅰ)求的值及函数的单调递增区间; (Ⅱ)当时,求函数的取值范围. 10、(乐山市第一中学2014届高三10月月考)某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度=4m,仰角∠ABE=,∠ADE=。 (1)该小组已经测得一组、的值,tan=1.24,tan=1.20,请据此算出H的值; (2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使与之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,-最大? 11、(泸州市2014届高三第一次教学质量诊断) 在△ABC中,角、、的对边分别为、、,设S为△ABC的面积,满足 . (Ⅰ)求角C的大小; (Ⅱ)若,且,求的值. 12、(绵阳市高中2014届高三11月第一次诊断性考试) 已知函数 (I)求函数f(x)的定义域及最大值; (II)求使f(x)≥0成立的x的取值集合。 13、(绵阳市高中2014届高三11月第一次诊断性考试) 安通驾校拟围着一座山修建一条环形训练道路OASBCD,道路的平面图如图所示(单位:km),已知曲线ASB为函数的图象,且最高点为 S(1,2),折线段AOD为固定线路,其中AO=,OD=4,折线段BCD为可变线路,但为保证驾驶安全,限定∠BCD=120°。 (I)求的值; (II)应如何设计,才能使折线段道路BCD最长? 14、(什邡中学高中2014届高三上学期第二次月考) 已知函数的周期为,其中. (Ⅰ)求的值及函数的单调递增区间; (Ⅱ)在中,设内角A、B、C所对边的长分别为a、b、c,若,,f(A)=,求b的值. 15、(资阳市2014届高三上学期第一次诊断性考试) 已知函数(). (Ⅰ)求在内的单调递增区间; (Ⅱ)在中,为锐角,且,,是边上一点,,试求的最大值. 2012-2013年联考题 (一) 1【云南省昆明一中2013届高三新课程第一次摸底测试理】在△ABC中的内角A、B、C所对的边分别为a,b,c,若则△ABC的形状为 A.直角三角形 B.锐角三角形 C.等边三角形 D.等腰直角三角形 2.【云南省昆明一中2013届高三新课程第一次摸底测试理】函数的简图是 3.【云南省昆明一中2013届高三新课程第一次摸底测试理】化简则 A. B. C. D. 4.【云南省玉溪一中2013届高三第三次月考 理】函数为增函数的区间是( ) A. B. C. D. 5.【云南省玉溪一中2013届高三第四次月考理】已知函数的图象如图所示,则等于( ) A. B. C. D. 6.【云南省玉溪一中2013届高三第四次月考理】在中,若,则的形状是( ) A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形 7.【云南省玉溪一中2013届高三上学期期中考试理】函数的最大值为 ( ) A. B. C. D. 8.【云南师大附中2013届高三高考适应性月考卷(三)理科】对于函数,下列说法正确的是( ) A.该函数的值域是 B.当且仅当时, C.当且仅当时,该函数取最大值1 D.该函数是以为最小正周期的周期函数 9.【天津市耀华中学2013届高三第一次月考理科】在△ABC中,a,b,c分别是角A,B,C的对边,a=,b=,且1+2cos(B+C)=0,则BC边上的高等于 A、-1 B、+1 C、 D、 10.【天津市耀华中学2013届高三第一次月考理科】把函数的图象上所有的点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是 A、 B、 C、 D、 11.【天津市新华中学2012届高三上学期第二次月考理】 把函数的图象向右平移个单位,再把所得图象上各点的横坐标缩短到原来的一半,则所得图象对应的函数解析式是 A. y=sin(4x+) B. y=sin(4x+) C. y=sin4x D. y=sinx 12.【天津市天津一中2013届高三上学期一月考 理】在∆ABC中,A,B,C为内角,且,则∆ABC是 A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形 13.【天津市天津一中2013届高三上学期一月考 理】函数f(x)=sin2x-4sin3xcosx(x∈R)的最小正周期为 A. B. C. D.π 14.【天津市天津一中2013届高三上学期一月考 理】设函数(x∈R),则f(x) A.在区间[-π,]上是减函数 B.在区间上是增函数 C.在区间[,]上是增函数 D.在区间上是减函数 15.【山东省烟台市莱州一中2013届高三10月月考(理)】和是方程的两根,则p、q之间的关系是 A. B. C. D. 16.【山东省烟台市莱州一中2013届高三10月月考(理)】已知、都是锐角,则= A. B. C. D. 17.【山东省烟台市莱州一中2013届高三10月月考(理)】如果函数的图像关于点中心对称,那么的最小值为 A. B. C. D. 18.【山东省烟台市莱州一中2013届高三10月月考(理)】函数的图象如下,则等于 A.0 B.503 C.1006 D.2012 19.【山东省烟台市莱州一中20l3届高三第二次质量检测 (理)】已知,则等于 A. B. C. D. 20.【山东省烟台市莱州一中20l3届高三第二次质量检测 (理)】函数(><)的图象如图所示,为了得到的图象,可以将的图象 A.向右平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向左平移个单位长度 21.【山东省烟台市莱州一中20l3届高三第二次质量检测 (理)】2009年北京庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为10米,则旗杆的高度为______米。 22.【山东省烟台市莱州一中2013届高三10月月考(理)】若则_________. 23.【山东省烟台市莱州一中2013届高三10月月考(理)】关于函数有下列命题: ①函数的周期为; ②直线是的一条对称轴; ③点是的图象的一个对称中心; ④将的图象向左平移个单位,可得到的图象.其中真命题的序号是______.(把你认为真命题的序号都写上) 24.【天津市天津一中2013届高三上学期一月考 理】已知,且,则_________. 25.【天津市天津一中2013届高三上学期一月考 理】函数(x∈R)的图象为C,以下结论中: ①图象C关于直线对称; ②图象C关于点对称; ③函数f(x)在区间内是增函数; ④由的图象向右平移个单位长度可以得到图象C. 则正确的是 .(写出所有正确结论的编号) 26.【天津市新华中学2012届高三上学期第二次月考理】 在△ABC中,若sinA=2sinBcosC则△ABC的形状为________。 27.【天津市耀华中学2013届高三第一次月考理科】函数为常数,A>0, >0)的部分图象如图所示,则f(0)的值是 ; 28.【天津市耀华中学2013届高三第一次月考理科】在△ABC中,a,b,c分别是角A,B,C的对边,若,则的值为 ; 29.【云南师大附中2013届高三高考适应性月考卷(三)理科】在锐角△ABC中,角A、B、C所对的边分别为a、b、c,若b=2,B=且sin2A+sin(A+C)=sinB,则△ABC的面积为 。 30【山东省临沂市2013届高三上学期期中考试理】在△ABC中,若则的值为 . 31.【 北京四中2013届高三上学期期中测验数学(理)】已知函数,给出下列四个说法: ①若,则; ②的最小正周期是; ③在区间上是增函数; ④的图象关于直线对称. 其中正确说法的序号是______. 32.【 北京四中2013届高三上学期期中测验数学(理)】定义一种运算 ,令,且, 则函数的最大值是______. 33.【山东省德州市乐陵一中2013届高三10月月考数学理】若α是锐角,且的值是 . 34.【山东省德州市乐陵一中2013届高三10月月考数学理】函数的图象如图所示,则的值等于 35.【山东省实验中学2013届高三第一次诊断性测试理】在△ABC中,角A,B,C的对边为a,b,c,若,则角A= 。 36.【山东省德州市乐陵一中2013届高三10月月考数学理】如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得,CD=30,并在点C测得塔顶A的仰角为60.则塔高AB=__________. 37.【山东省聊城市东阿一中2013届高三上学期期初考试 】在△ABC中,若∠A:∠B:∠C=1:2:3,则 38.【山东省聊城市东阿一中2013届高三上学期期初考试 】已知 54【山东省临沂市2013届高三上学期期中考试理】已知下列四个命题: ①若; ②函数是奇函数; ③“”是“”的充分不必要条件; ④在△ABC中,若,则△ABC是直角三角形. 其中所有真命题的序号是 . 39.【山东省实验中学2013届高三第二次诊断性测试 理】在中,,且,则此三角形为 . 40.【山东省师大附中2013届高三12月第三次模拟检测理】在中,依次成等比数列,则B的取值范围是 41.【山东省烟台市2013届高三上学期期中考试理】 在中,若,则__________. 42.【山东省烟台市2013届高三上学期期中考试理】函数 的单调递增区间为 (二) 1.【山东省泰安市2013届高三上学期期中考试数学理】(本小题满分12分) 已知函数,直线是函数的图像的任意两条对称轴,且的最小值为. (I)求的值; (II)求函数的单调增区间; (III)若,求的值. 2.【山东省师大附中2013届高三12月第三次模拟检测理】(本题满分12分)设函数, (Ⅰ)求的周期和最大值 (Ⅱ)求的单调递增区间 3.【山东省师大附中2013届高三12月第三次模拟检测理】(本题满分12分) 在中, (Ⅰ)若三边长构成公差为4的等差数列,求的面积 (Ⅱ)已知是的中线,若,求的最小值 4.【山东省师大附中2013届高三上学期期中考试数学理】(本题满分12分)已知函数 (I)求的最小正周期和单调递增区间; (II)当时,求函数的最大值和最小值及相应的的值. 5.【山东省师大附中2013届高三上学期期中考试数学理】(本题满分12分)已知的三内角A,B,C所对三边分别为a,b,c,且 (I)求tanA的值; (II)若的面积,求a的值. 6.【山东省师大附中2013届高三上学期期中考试数学理】(本题满分12分)设函数. (I)当时,求函数的单调区间; (II)当时,求所有极值的和. 7.【山东省实验中学2013届高三第三次诊断性测试理】(本小题满分12分)在内, 分别为角A,B,C所对的边,a,b,c成等差数列,且a=2c。 (1) 求的值;(Ⅱ)若,求b的值。 8.【山东省青岛市2013届高三上学期期中考试理】(本小题满分12分) 已知向量,, 设函数的图象关于直线对称,其中为常数,且. (Ⅰ)求函数的表达式; (Ⅱ)若将图象上各点的横坐标变为原来的,再将所得图象向右平移个单位,纵坐标不变,得到的图象, 若关于的方程在区间上有且只有一个实数解,求实数的取值范围. 9.【山东省青岛市2013届高三上学期期中考试理】(本小题满分12分) 在中,分别是角的对边,已知. (Ⅰ)若,求的大小; (Ⅱ)若,的面积,且,求. 10.【北京市东城区普通校2013届高三12月联考数学(理)】(本小题满分分) 已知:在中, 、、分别为角、、所对的边,且角为锐角, (Ⅰ)求的值; (Ⅱ)当,时,求及的长. 11.【北京市东城区普通校2013届高三12月联考数学(理)】(本小题满分分) 已知:函数的部分图象如图所示. (Ⅰ)求 函 数的 解 析 式; (Ⅱ)在△中,角的 对 边 分 别 是,若的 取 值 范 围. 12.【 北京四中2013届高三上学期期中测验数学(理)】 (本小题满分13分) 如图,在平面直角坐标系中,以轴为始边作两个锐角,它们的终边分别与单位圆交于两点.已知的横坐标分别为. (1)求的值; (2)求的值. 13.【 北京四中2013届高三上学期期中测验数学(理)】(本小题满分13分) 已知函数. (1)求函数图象的对称轴方程; (2)求的单调增区间. (3)当时,求函数的最大值,最小值. 14.【 山东省滨州市滨城区一中2013届高三11月质检数学理】设的内角A、B、C的对应边分别为已知 (1)求的边长。 (2)求的值 15.【 山东省滨州市滨城区一中2013届高三11月质检数学理】 (本题满分12分) 在△ABC的三个内角A、B、C所对的边分别a、b、c, 设函数 (1)求角C的大小; (2)求函数的单调递增区间 16.【山东省德州市乐陵一中2013届高三10月月考数学理】(本小题满分12分) 已知 (1) 求的值. (2)求 的值 17.【山东省德州市乐陵一中2013届高三10月月考数学理】(本小题满分12分) 在中,角所对的边为已知. (Ⅰ)求的值; (Ⅱ)若的面积为,且,求的值. 18.【山东省聊城市东阿一中2013届高三上学期期初考试 】(本小题满分14分) 已知,设函数 2,4,6 (1)求的最小正周期及单调递增区间; (2)当时,求的值域. 19.【山东省聊城市东阿一中2013届高三上学期期初考试 】(本小题满分12分)已知函数. (1)求的值; (2)若对于任意的,都有,求实数的取值范围. 20【山东省聊城市东阿一中2013届高三上学期期初考试 】(本小题满分12分)在中,角所对的边为,已知。 (1)求的值; (2)若的面积为,且,求的值。 2011-2012年联考题 1、(2012滨州二模)函数f(x)=sin()(其中)的图象如图所求,为了得到g(x)=sin的图象,可以将f(x)的图象 (A)向右平移个单位长度 (B)向右平移个单位长度 (C)向左平移个单位长度 (D)向左平移个单位长度 2、(2012滨州二模)函数y=(-)的图象大致为 3、(2012德州二模)设函数,则下列结论正确的是 A.把的图象向左平移个单位,得到一个偶函数的图象 B.的图象关于点对称 C.的最小正周期为,且在上为增函数 D.f(x)的图象关于直线x=对称 4、(2012德州一模)已知函数的最大值为4,最小值为0,两条对称轴间的最短距离为,直线是其图象的一条对称轴,则符合条件的解析式是( ) A. B. C. D. 5、(2012济南3月模拟)函数的最小正周期是 A. B. C. 2π D. 4π 6、(2012济南三模)如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”. 给出下列函数: ①; ②; ③; ④. 其中“同簇函数”的是( ) A.①② B.①④ C.②③ D.③④ 9、(2012临沂二模)函数的部分图象如图,设是图象的最高点,是图象与轴的交点,则 (A) (B) (C) (D) 10、(2012临沂二模)已知船在灯塔北偏东处,且船到灯塔的距离为2km,船在灯塔北偏西处,、两船间的距离为3km,则B船到灯塔的距离为____________km。 11、(2012青岛二模)已知函数,,,那么下面命题中真命题的序号是 ①的最大值为 ② 的最小值为 ③在上是增函数 ④ 在上是增函数 A.①③ B.①④ C.②③ D.②④ 12、(2012青岛二模)若则 . 13、(2012青岛3月模拟)将函数的图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将所得图象向左平移个单位,则所得函数图象对应的解析式为 A. B. C. D. 14、(2012日照5月模拟)要得到函数的图象,可以将函数的图象 (A)沿轴向左平移个单位 (B)沿向右平移个单位 (C)沿轴向左平移个单位 (D)沿向右平移个单位 15、(2012泰安一模)函数(为常数,A>0, >0)的部分图象如图所示,则的值是 ▲ . 16、(2012烟台二模)已知倾斜角为的直线与直线平行,则tan的值为 A. B. C. D. 17、(2012烟台二模)函数y=x+sin,的大致图象是 18、(2012滨州二模)在△ABC中,内角A、B、C的对边分别为a、b、c,已知a2+b2=6abcosC,且sin2c=2sinAsinB。 (I)求角C的大小; (II)设函数f(x)=sin-,且f(x)图象上相邻两最高点间的距离为,求f(A)的取值范围。 19、(2012德州二模)在△ABC中,角A,B,C的对边分别是a、b、c,已知向量 且m//n. (I)求角A的大小; (II)若面积的最大值。 20、(2012德州一模)已知函数 (I)求函数的最小正周期及在区间上的值域; (Ⅱ)在ABC中,角A、B、C所对的边分别是a、b、c,又的面积等于3,求边长a的值. 21、(2012济南3月模拟)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos,=3. (1) 求△ABC的面积; (2) 若c=1,求a、sinB的值. 22、(2012济南三模)已知函数的图象经过点 (1)求实数的值; (2)求函数的周期及单调增区间. 23、(2012莱芜3月模拟)已知的三个内角所对的边分别为a,b,c,向量, ,且. (Ⅰ)求角的大小; (Ⅱ)若向量,试求的取值范围. 24、(2012青岛二模)已知向量,设函数,若函数的图象与的图象关于坐标原点对称. (Ⅰ)求函数在区间上的最大值,并求出此时的值; (Ⅱ)在中,分别是角的对边,为锐角,若,,的面积为,求边的长. 25、(2012青岛3月模拟)已知锐角中内角、、的对边分别为、、,,且. (Ⅰ)求角的值; (Ⅱ)设函数,图象上相邻两最高点间的距离为,求的取值范围. 26、(2012日照5月模拟)已知函数,且函数的最小正周期为。 (Ⅰ)求函数的解析式; (Ⅱ)在中,角A,B,C所对的边分别为,若,且,试求的值。 27、(2012威海二模)已知函数(),直线,是图象的任意两条对称轴,且的最小值为. (I)求的表达式; (Ⅱ)将函数的图象向右平移个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数的图象,若关于的方程,在区间上有且只有一个实数解,求实数的取值范围. 28、(2012烟台二模) 在锐角三角形ABC中,a、b、c分别是角A、B、C的对边,向量 且m//n. (1)求角A的大小; (2)求函数的值域. 最新模拟 【江西省新钢中学2012届高三第一次考试】设函数为 A.周期函数,最小正周期为 B.周期函数,最小正周期为 C.周期函数,最小正周期为 D.非周期函数 【江西省新钢中学2012届高三第一次考试】5.E,F是等腰直角△ABC斜边AB上的三等分点,则 A. B. C. D. 【江西省新钢中学2012届高三第一次考试】6.若,, ,,则 A. B. C. D. 【江西省新钢中学2012届高三第一次考试】7.如图,在△中,是边上的点,且,则的值为 A. B. C. D. 【江西省新钢中学2012届高三模拟】12.已知 则的值为__________ 【河北衡水中学2012届高三模拟】13.在中,,则的最大值为 。 【2012唐山市高三模拟统一考试理】的值为( ) A. B. C. D.2 【2012厦门市高三模拟质检理】对任意x、y∈R,恒有sinx+cosy=2sin()cos(),则sin等于 A. B. C. D. 【2012厦门市高三质检理】已知函数f(x)=Asin()(A>0,0<<)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0)。若∠PRQ=,则y=f(x) 的最大值及的值分别是 A.2, B., C., D. 2, 【2012年石家庄市高中毕业班教学质检1理】下列函数中,周期是,又是偶函数的是 A.y=sinx B.y=cosx C.y=sin2x D.y=cos2x 【2012武昌区高三年级元月调研理】给出以下4个命题: ①函数的最小正周期是; ②终边在y轴上的角的集合是; ③把函数的图象向右平移个单位得到函数的图象; ④函数在区间上是减函数. 其中真命题的个数是 ( ) A.1 B.2 C.3 D.4 【2012年西安市高三年级第四次质检理】设,则函数的 A.图像关于直线对称 B.图像关于直线对称 C.图像关于直线对称 D.图像关于直线对称 【2012唐山市高三上学期模拟统一考试理】函数 ( ) A.在单调递减 B.在单调递增 C.在单调递减 D. 在单调递增 【山东省日照市2012届高三模拟理】(6)函数的图象如图所示,为了得到的图象,则只需将的图象 (A)向右平移个长度单位 (B)向右平移个长度单位 (C)向左平移个长度单位 (D)向左平移个长度单位 【山东实验中学2012届高三第一次诊断性考试理】8. 要得到函数的图像,只需将函数的图像 ( ) (A).向左平移个单位 (B).向右平移个单位 (C).向左平移个单位 (D).向右平移个单位[高&考%资(源#网] 【2012厦门模拟质检理7】已知函数f(x)=sin(ωx+)(ω>0),将函数y=f(x)的图象向右平移个单位长度后,所得图象与原函数图象重合ω最小值等于 A. B.3 C.6 D.9 【2012粤西北九校联考理4】如图,设A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点 C,测出AC的距离为50m,∠ACB = 45°,∠CAB = 105°后,就可以计算出A、B两点的距离为( ) 【2012宁德质检理3】为了得到函数的图象,可将函数的图象 ( ) A.向右平移个单位 B.向左平移个单位 C.向右平移个单位 D.向左平移个单位 【2012宁德质检理8】已知的面积为,则的周长等于 ( ) A. B. C. D. B A C 【2012韶关第一次调研理4】为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩(如图),要测算两点的距离,测量人员在岸边定出基线,测得,,就可以计算出两点的距离为( ) A. B. C. D. 【2012海南嘉积中学模拟理13】设为第一象限的角,,则 . 【2012黑龙江绥化市一模理3】若,则的值为( ) A.2 B.3 C.4 D.6 【2012 浙江瑞安模拟质检理5】设,则的值为( ) A. B. C. D. 【2012 浙江瑞安模拟质检理13】函数的部分图象如右图所示,设是图象的最高点,是图象与轴的交点,则= . 【2012延吉市质检理4】在中,若则角B的大小为 ( ) A.30° B.45° C.135° D.45°或135° 【2012浙江宁波市模拟理】若,且,则 . 【2012安徽省合肥市质检理】已知,则= ( ) A. B. C. D. 【2012山东青岛市模拟理】已知,则的值为 A. B. C. D. 【2012山东青岛市模拟理】已知函数为奇函数,该函数的部分图象如图所示,是边长为的等边三角形,则的值为 A. B. C. D. 【2012吉林市模拟质检理】已知是第四象限角,且,则( ) A. B. C. D. 【2012吉林市模拟质检理】为了得到函数的图象,只需将函数的图象 A.向左平移个长度单位 B.向右平移个长度单位 C.向左平移个长度单位 D.向右平移个长度单位 【2012广东佛山市质检理】把函数的图象上所有的点向左平移个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为( ) A. B. C. D. 【2012河南郑州市质检理】函数图象的一条对称轴是( ) A. B. C. D. 【2012北京海淀区模拟理】函数的部分图象如图所示,那么 (A) (B) (C) (D) 【2012延吉市质检理12】已知,,的最小值为,则正数 . 【2012金华十校高三上学期模拟联考理】已知,则= ; 【2012唐山市高三上学期模拟统一考试理】在中,边上的高为则AC+BC= 。 【2012厦门市高三上学期模拟质检理】函数f(x)=sin(x+)-cos(x+),x∈[0,2π]的单调递减区间是 。 【2012黄冈市高三上学期模拟考试理】已知中,,那么角A等于 。 【2012年石家庄市高中毕业班教学质检1理】某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D. (I)求AB的长度; (Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素, 小李、小王谁的设计使建造费用最低,请说明理由. 【2012厦门市高三上学期模拟质检理】在△ABC中,a、b、c分别是三个内角A、B、C的对边,a=2,sin且△ABC的面积为4 (Ⅰ)求cosB的值; (Ⅱ)求边b、c的长。 【2012江西师大附中高三模拟理】已知向量,, (1)若,求的值; (2)在中,角的对边分别是,且满足,求函数的取值范围. 【2012黄冈市高三模拟考试理】已知函数为偶函数,其图象上相邻的两个最低点间的距离为。 (1)求的解析式; (2)若,求的值。 【2012武昌区高三年级元月调研理】设的内角A、B、C所对的边分别为a、b、c,已知,E为边AB的中点。 (I)求的周长; (II)求的内切圆的半径与的面积. 【2012浙江宁波市模拟理科】已知,满足. (I)将表示为的函数,并求的最小正周期; (II)已知分别为的三个内角对应的边长,若,且,求的取值范围. 【2012吉林市模拟质检理】在某海岸A处,发现北偏东方向,距离A处n mile的B处有一艘走私船在A处北偏西的方向,距离A处n mile的C处的缉私船奉命以n mile/h的速度追截走私船. 此时,走私船正以5 n mile/h的速度从B处按照北偏东方向逃窜,问缉私船至少经过多长时间可以追上走私船,并指出缉私船航行方向. A C B · · 【2012江西南昌市调研理】已知向量=sin2C,其中A,B,C分别为△ABC的三边a,b,c所对的角. (1)求角C的大小; (2)已知A=75°,c=(cm),求△ABC的面积 【2012 广东佛山市质检理】在△中,角、、的对边分别为,若,且. (1)求的值; (2)若,求△的面积. 【2012北京海淀区模拟理】在中,角,,所对的边分别为,,, , . (Ⅰ)求的值; (Ⅱ)若,求边的长. 【2012广东韶关市调研理】已知函数. (1)求的周期和单调递增区间; (2)说明的图象可由的图象经过怎样变化得到. 2011年联考题 题组一 选择题 1.(安徽省百校论坛2011届高三第三次联合考试理) 已知等于 ( ) A. B. C. D.— 2.(浙江省金丽衢十二校2011届高三第一次联考文)函数的最大值是 ( ) A. B. C.2 D.1 3.(山东省莱阳市2011届高三上学期期末数学模拟6理)已知,则的值是( ) A、 B、 C、 D、 4.(湖南省嘉禾一中2011届高三上学期1月高考押题卷)在区间上随机取一个数的值介于0到之间的概率为 ( ) A. B. C. D. 5. (湖北省补习学校2011届高三联合体大联考试题理) 已知下列不等式中必成立的是( ) A. B. C. D. 6.(河南省鹿邑县五校2011届高三12月联考理)函数的图像为C,如下结论中正确的是 ( ) A.图像C关于直线对称 B.图像C关于点对称 C.函数在区间内是增函数 D.由的图像向右平移个单位长度可以得到图像C。 7. (河南省辉县市第一高级中学2011届高三12月月考理)若则 A. B.2 C. D.-2 8. (北京四中2011届高三上学期开学测试理科试题) 已知,则等于( ) A.7 B. C. D. 9.(福建省三明一中2011届高三上学期第三次月考理) 已知函数,给出下列四个命题: ①若 ②的最小正周期是; ③在区间上是增函数; ④的图象关于直线对称; ⑤当时,的值域为 其中正确的命题为 ( ) A.①②④ B.③④⑤ C.②③ D.③④ 10.(浙江省温州市啸秋中学2010学年第一学期高三会考模拟试卷)函数的最小值是 A. B. C. D. 11.(浙江省嵊州二中2011届高三12月月考试题文) 函数的最大值为 ( ) (A) (B) (C) (D) 12.(山东省日照市2011届高三第一次调研考试文)已知则的值为 (A) (B) (C) (D) 13. (福建省四地六校2011届高三上学期第三次联考试题理)已知,且其中,则关于的值,在以下四个答案中,可能正确的是 ( ) A. B.3 或 C. D.或 14.(甘肃省甘谷三中2011届高三第三次检测试题)的值为( ) A. B. C. D. 15. (甘肃省甘谷三中2011届高三第三次检测试题) 若,则( ) A. B. C. 0 D. 0或 16.(福建省四地六校2011届高三上学期第三次联考试题理)给出下面的3个命题:(1)函数的最小正周期是;(2)函数在区间上单调递增;(3)是函数的图象的一条对称轴. 其中正确命题的个数是( ) A.0 B.1 C.2 D.3 17.(甘肃省甘谷三中2011届高三第三次检测试题) 已知函数的最小正周期为,则该函数的图象( ) A.关于点对称 B.关于直线对称 C.关于点对称 D.关于直线对称 18.(山东省莱阳市2011届高三上学期期末数学模拟6理)已知函数的最大值是4,最小值是0,最小正周期是,直线是其图象的一条对称轴,则下面各式中符合条件的解析式是( ) A. B. C. D. 19.(吉林省东北师大附中2011届高三上学期第三次模底考试理) 已知函数的最小正周期为,为了得到函数 的图象,只要将的图象 ( ) A. 向左平移个单位长度 B. 向右平移个单位长度 C. 向左平移个单位长度 D. 向右平移个单位长度 20.(湖南省嘉禾一中2011届高三上学期1月高考押题卷)函数图象如右图,则函数的单调递增区间为( ) A. B. C. D. 21.(湖北省涟源一中、双峰一中2011届高三第五次月考理)下列函数中,周期为,且在上为减函数的是 ( ) A. B. C. D. 22.(湖北省部分重点中学2011届高三第二次联考试卷)函数的图像如图所示,,则的值为 ( ) A. B. C. D. 23.(黑龙江省佳木斯大学附属中学2011届高三上学期期末考试理) 函数 ,给出下列四个命题 (1)函数在区间上是减函数; (2)直线是函数图象的一条对称轴; (3)函数的图象可由函数的图象向左平移而得到; (4)若 ,则 的值域是 其中正确命题的个数是 ( ) A.1 B.2 C.3 D.4 24.(黑龙江省哈九中2011届高三期末考试试题理)将函数的图像按向量平移之后所得函数图像的解析式为 ( ) A. B. C. D. 25.(广西北海二中2011届高三12月月考试题理)的图象是 ( ) A.关于原点成中心对称 B.关于轴成轴对称 C.关于点成中心对称 D.关于直线成轴对称 26.(河南省辉县市第一高级中学2011届高三12月月考理)已知函数的部分图象如图所示,则函数的解析式为 A. B. C. D. 27.(广东省高州市南塘中学2011届高三上学期16周抽考理) 已知函数的最大值为2,则的最小正周期为 ( ) A. B. C. D. 28.(北京龙门育才学校2011届高三上学期第三次月考)函数是 ( ) A.最小正周期为的奇函数 B.最小正周期为的偶函数 C.最小正周期为的奇函数 D.最小正周期为的偶函数 29.(福建省厦门外国语学校2011届高三11月月考理)函数 ,给出下列四个命题 (1)函数在区间上是减函数; (2)直线是函数图象的一条对称轴; (3)函数 的图象可由函数的图象向左平移而得到; (4)若 ,则 的值域是 其中正确命题的个数是 ( ▲ ) A.1 B.2 C.3 D.4 30.(甘肃省甘谷三中2011届高三第三次检测试题) 若△的内角满足,则= ( ) A. B. C. D. 16题图 31.(广东省清远市清城区2011届高三第一次模拟考试理)函数(其中)的图象如图所示,为了得到的图像,则只要将的图像( ) A.向右平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向左平移个单位长度 32.(广西北海二中2011届高三12月月考试题理)函数的图象按向平移后的解析式为 ( ) A B C D 33.(河南省焦作市部分学校2011届高三上学期期终调研测试理)已知函数 ,下面结论错误的是 A.函数的最小正周期为 B.函数是奇函数 C.函数的图象关于直线对称 D.函数在区间上是减函数 34.(贵州省遵义四中2011届高三第四次月考理))函数的图象为,以下三个命题中,正确的有( )个 ①图象关于直线对称; ②函数在区间内是增函数; ③由的图象向右平移个单位长度可以得到图象. A.0 B.1 C.2 D.3 35.(河南省长葛第三实验高中2011届高三期中考试理) 函数的图象如下图,则 ( ) A. B. C. D. 填空题 36.(重庆市重庆八中2011届高三第四次月考文) 在中,如果=,则此三角形最大角的余弦值是 . 37.(重庆市南开中学高2011级高三1月月考文) 若 。 38.(山东省日照市2011届高三第一次调研考试文)关于函数有下列命题:①函数的周期为; ②直线是的一条对称轴;③点是的图象的一个对称中心;④将的图象向左平移个单位,可得到的图象.其中真命题的序号是 .(把你认为真命题的序号都写上) 39.(北京龙门育才学校2011届高三上学期第三次月考)已知是第二象限的角,,则__________。 40.(北京四中2011届高三上学期开学测试理科试题)的值域为___________。 41.(北京五中2011届高三上学期期中考试试题理)函数的最小正周期为 42.(福建省安溪梧桐中学2011届高三第三次阶段考试理)若是锐角,且,则的值是 . 43.(福建省四地六校2011届高三上学期第三次联考试题理)已知为第二象限角,且P( x,)为其终边上一点,若cos=则x的值为 44.(甘肃省甘谷三中2011届高三第三次检测试题)已知,sin()=- 则= 45.(福建省安溪梧桐中学2011届高三第三次阶段考试理)下图展示了一个由角的区间(0,)到实数集R的映射过程:区间(0,)中的角始边落在OA上,则终边对应半圆弧AB上的点M,如图1;将半圆弧围成一个椭圆,使两端点A、B恰好重合,如图2;再将这个椭圆放在平面直角坐标系中,使其椭圆中心在y轴上,点A的坐标为,如图3中直线与x轴交于点,则的象就是n,记作. 下列说法中正确命题的序号是 .(填出所有正确命题的序号) ①; ②是奇函数; ③是定义域上的单调函数; 2 0 2 6 x y ④的图象关于点对称 ; ⑤的图象关于y轴对称 46.(甘肃省甘谷三中2011届高三第三次检测试题) 函数的图象如图所示, 则的值等于 . 47.(广东省新兴惠能中学2011届高三第四次月考理)已知是第二象限角, ,则 简答题 48.(甘肃省甘谷三中2011届高三第三次检测试题) (12分)已知函数,. (I)求的最大值和最小值;(II)若不等式在上恒成立,求实数的取值范围 49.(山东省日照市2011届高三第一次调研考试文)(本小题满分12分) 设函数. (Ⅰ)求的最小正周期; (Ⅱ)求函数在上的值域. 50.(重庆市南开中学高2011级高三1月月考文) (13分) 已知向量 (1)当时,若,求的值; (2)定义函数的最小正周期及最大值。 51.(湖南省嘉禾一中2011届高三上学期1月高考押题卷) 已知函数 (Ⅰ)求函数的最小正周期和图象的对称轴方程 (Ⅱ)求函数在区间上的值域 52.(北京龙门育才学校2011届高三上学期第三次月考)(理科做)(本小题满分13分)已知向量=, 。 (Ⅰ)求函数的解析式,并求其单调增区间; (Ⅱ)若集合,试判断 与集合的关系。 53.(甘肃省天水一中2011届高三上学期第三次月考试题理)(10分)求值(每小题5分) (1). (2)已知,求的值。 54.(浙江省嵊州二中2011届高三12月月考试题文)(本小题满分14分)已知中的内角的对边分别为,定义向量, 且. (Ⅰ)求函数的单调递增区间; (Ⅱ)如果,求的面积的最大值 55.(山东省莱阳市2011届高三上学期期末数学模拟6理)(本小题满分12分) 已知函数, (I)求函数的最小值和最小正周期; (II)设的内角的对边分别为,且,,若向量与向量共线,求的值. 56.(湖北省补习学校2011届高三联合体大联考试题理) (12分)设 (1)若,求的值 (2)若,求在上的递减区间 57.(福建省安溪梧桐中学2011届高三第三次阶段考试理)(本小题满分13分) 设函数的图象经过点. (Ⅰ)求的解析式,并求函数的最小正周期和单调递增区间 (Ⅱ)若,其中是面积为的锐角的内角,且, 求和的长. 58、(福建省三明一中2011届高三上学期第三次月考理)(本题满分13分) A、B是直线图像的两个相邻交点,且 (I)求的值; (II)在锐角中,a,b,c分别是角A,B,C的对边,若 的面积为,求a的值. 59.(广东省华附、中山附中2011届高三11月月考理) (12分)已知, (Ⅰ)求函数的最小正周期; (Ⅱ) 当,求函数的零点. 60.(广东省惠州三中2011届高三上学期第三次考试理)(12分)已知函数. (Ⅰ)求函数的最小正周期; (Ⅱ)若函数在[-,]上的最大值与最小值之和为,求实数的值. 61.(河南省长葛第三实验高中2011届高三期中考试理)(本小题满分12分) 已知函数为常数). (1)求函数的最小正周期; (2)求函数的单调递增区间; (3) 若时,的最小值为,求的值. 题组二 一、选择题 1.(成都市玉林中学2010—2011学年度)函数,已知在 时取得极值,则= (A)4 (B)3 (C)5 (D)2 2.(成都市玉林中学2010—2011学年度) (A) (B) (C)— (D)— 3. (成都市玉林中学2010—2011学年度)已知定义域为R的函数在上为减函数,且函数为偶函数,则 A. B. C. D. 4.(成都市玉林中学2010—2011学年度)的图象是: (A)关于原点成中心对称 (B)关于轴成轴对称 (C)关于点成中心对称 (D)关于直线成轴对称 D C P B A x y 0 4 9 14 5.(江西省2011届高三文)直角梯形ABCD,如图1,动点P从B点出发,由B→C→D→A沿边运动,设动点P运动的路程为x,ΔABP面积为,已知图象如图2,则ΔABC面积为( ) 图1 图2 A.10 B.16 C.18 D.32 6.(江西省2011届高三理)若函数f(x)=x- 在(1,+∞)上是增函数,则实数p的取值范围是 A.[-1,+∞) B.[1,+∞) C.(-∞,-1] D.(-∞,1] 7.(四川省成都市玉林中学2011届高三理)的图象是: A.关于原点成中心对称 B.关于轴成轴对称 C.关于点成中心对称 D.关于直线成轴对称 8.(浙江省桐乡一中2011届高三理)要得到函数y=cos2x的图象,只需将函数y=cos(2x-)的图象 (A)向右平移个单位 (B)向左平移个单位 (C)向右平移个单位 (D)向左平移个单位 9.(四川省成都外国语学校2011届高三10月文)同时具有性质:“①对任意,恒成立;②图象关于直线对称;③在上是增函数”的函数可以是( ) A. B. C. D. 10.(四川省成都外国语学校2011届高三10月文).已知函数的图象在点A处的切线的斜率为4,则函数的最大值是( ) A. 1 B. 2 C. D. 11.(2011湖南嘉禾一中)的最大值 和最小正周期分别是 ( ) A. B.2,2π C.,2π D.1,2π 12.(北京四中2011届高三上学期开学测试理科试题)函数的图象为C,则下列论断中,正确论断的个数是( ) (1)图象C关于直线对称; (2)函数在区间内是增函数; (3)由函数的图象向右平移个单位长度可以得到图象C. A.0 B.1 C.2 D.3 13.(北京五中2011届高三上学期期中考试试题理)将函数的图象向左平移个单位长度,向上平移1个单位长度,所得图象对应的函数解析式是( ) 14.(福建省安溪梧桐中学2011届高三第三次阶段考试理)将函数的图象向右平移个单位,再将图象上每一点的横坐标缩短到原来的倍,所得图象关于直线对称,则的最小正值为 ( ) A. B. C. D. 15.(福建省惠安荷山中学2011届高三第三次月考理科试卷) 在同一直角坐标系中,的图象和直线的交点个数是( ) A. 0 B. 1 C. 2 D. 4 16.(福建省惠安荷山中学2011届高三第三次月考理科试卷) 函数 ,给出下列四个命题: (1)函数在区间上是减函数; (2)直线是函数图象的一条对称轴; (3)函数 的图象可由函数的图象向左平移而得到; (4)若 ,则 的值域是 。 其中正确命题的个数是 ( ) A.1 B.2 C.3 D.4 二、填空题 17.(江苏泰兴市重点中学2011届理)函数的最小正周期 18.(江苏泰兴市重点中学2011届理)函数在上的最小值等于 19.(江苏泰兴市重点中学2011届理)函数在上的单调增区间为 20.(江苏泰兴市重点中学2011届理)已知函数是奇函数,当时,,,则 _________ 21.(江苏泰兴市重点中学2011届理)设函数是定义在R上以3为周期的奇函数,若,,则a的取值范围是__________________________. 22.(江苏省2011届高三理)关于函数,有下列命题 ①其图象关于轴对称; ②当时,是增函数;当时,是减函数; ③的最小值是; ④在区间(-1,0)、(2,+∞)上是增函数 ⑤无最大值,也无最小值 其中所有正确结论的序号是 23.(湖南省嘉禾一中2011届高三上学期1月高考押题卷)函数的图象为,如下结论中正确的是_______ (写出所有正确结论的编号) ①图象关于直线对称; ②图象关于点对称; ③函数在区间内是增函数; ④由的图角向右平移个单位长度可以得到图象 24.(四川成都市玉林中学2010—2011学年度)已知函数.给出下列命题:①必是偶函数;②当时,的图像必关于直线x=1对称;③若,则在区间上是增函数;④有最大值. 其中正确的序号是 。 三、简答题 26.(江苏泰兴市重点中学2011届理)(本小题满分14分):已知函数 是奇函数,并且函数的图像经过点(1,3),(1)求实数的值;(2)求函数的值域 27.(江苏泰兴市重点中学2011届)(14分)已知 (1)若,求的值; (2)若,求的值。 28.(2011湖南嘉禾一中)(本小题满分12 分) 已知函数的最大值为1. (1)求常数a 的值; (2)求的单调递增区间; (3)求≥ 0 成立的x 的取值集合. 29.(2011湖南嘉禾一中)(本题满分13 分) 已知函数 (1)若在的图象上横坐标为的点处存在垂直于y 轴的切线,求a 的值; (2)若在区间(-2,3)内有两个不同的极值点,求a 取值范围; (3)在(1)的条件下,是否存在实数m,使得函数的图象与函数的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由. 30.(成都市玉林中学2010—2011学年度)(本题满分12分)已知向量a, b,若.(I)求函数的解析式和最小正周期; (II) 若,求的最大值和最小值. 31.(四川成都市玉林中学2010—2011学年度)(本题满分12分)已知向量a, b,若.(I)求函数的解析式和最小正周期; (II) 若,求的最大值和最小值. 32.(四川成都市玉林中学2010—2011学年度)(本题满分14分)已知二次函数,且满足 . (1)证明:函数的图象交于不同的两点A,B; (2)若函数上的最小值为9,最大值为21,试求的值; (3)求线段AB在轴上的射影A1B1的长的取值范围. 34.(江苏泰兴市重点中学2011届)(14分)设的内角A、B、C的对边长分别为a、b、c,且3+3-3=4bc . (Ⅰ) 求sinA的值; (Ⅱ)求的值. 35.(江苏泰兴市重点中学2011届)(16分)已知函数(其中常数),是奇函数。 (1)求的表达式; (2)讨论的单调性,并求在区间上的最大值和最小值。 36.(江苏泰兴市重点中学2011届理)(本题满分16分)设二次函数 在区间上的最大值、最小值分别是M、m,集合. (1)若,且,求M和m的值; (2)若,且,记,求的最小值. 2010年联考题 题组二(5月份更新) 一、选择题 1. (池州市七校元旦调研)如果函数的图像关于点中心对称,那么的最小值为( ) (A) (B) (C) (D) 2.(玉溪一中期中文)已知sin=,cos=,则角所在的象限是 ( ) A.第一象限. B. 第二象限. C. 第三象限. D. 第四象限. 3.(池州市七校元旦调研)已知是实数,则函数的图象不可能是 ( ) 4.(祥云一中三次月考理)在△ABC中,角A、B、C所对的边分别为a、b、c,已知B=,,c=2,则△ABC的面积为 A. B.1 C. D. 5. (肥城市第二次联考)若将函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为 A. B. C. D. 6.(祥云一中二次月考理)若关于的方程上恰有3个根,且最小根为则有 ( ) A. B. C. D. 7.(祥云一中三次月考理)使函数递减且函数递增的区间是 A.() B.()() C.()() D.()() 8.(祥云一中三次月考理)函数是 A.周期为的奇函数 B.周期为的偶函数 C.周期为2的奇函数 D.周期为2的偶函数 9. (三明市三校联考)设函数的最大值为3,则f(x)的图象的一条对称轴的方程是 ( ) A. B. C. D. 10.(祥云一中三次月考文)已知,则 A. B. C. D. 11. (哈师大附中、东北师大附中、辽宁省实验中学)函数的图象如下图,则( ) A. B. C. D. 12.(祥云一中三次月考文)已知函数,下面结论错误的是 A. 函数的最小正周期为2 B. 函数是奇函数 C.函数的图象关于直线=0对称 D. 函数在区间[0,]上是增函数 二、填空题 1.(肥城市第二次联考)已知,是第一象限角,则的值是: 。 2. (岳野两校联考)已知函数若对任意都有则=________. 3. (安庆市四校元旦联考)设函数的图象位于轴右侧所有的对称中心从左依次为,则的坐标是 。 4.(祥云一中二次月考理)如果且是第四象限的角,那么= 5.(祥云一中二次月考理)若,且,则 6.(昆明一中三次月考理)关于函数有下列命题: ① 的周期为π; ② x =是的一条对称轴; ③(,0)是的一个对称中心;④ 将的图象向左平移个单位,可得到的图象,其中正确的命题序号是 (把你认为正确命题的序号都写上). 7.(祥云一中三次月考文)已知 ,则 = . 8.(祥云一中三次月考理)y=f(x)是关于x=3对称的奇函数,f()=,, 若t=,则f(t)= . 题组一(1月份更新) 一、选择题 1.(2009昆明一中第三次模拟)若且,则是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 2、(2009玉溪市民族中学第四次月考)化简得-----------( ) A.sin B.cos C.1+cos2 D.1+sin2 3.(2009青岛一模)设函数,则下列结论正确的是 A.的图像关于直线对称 B.的图像关于点对称 C.把的图像向左平移个单位,得到一个偶函数的图像 D.的最小正周期为,且在上为增函数 4、(2009江门一模)已知,函数的图象关于直线对称,则的值可以是 A. B C. D. 5.(2009日照一模)已知函数,给出下列四个命题: ①若,则; ②的最小正周期是; ③在区间上是增函数; ④的图象关于直线对称 A.①②④ B.①③ C.②③ D.③④ 6.(2009牟定一中期中)已知是第三象限角,并且sin=,则等于 ( ) A. B C.- D.- 7.(2009南华一中12月月考)要得到一个奇函数,只需将函数的图象( ) A.向右平移个单位 B.向右平移个单位 C.向左平移个单位 D.向左平移个单位 8.(2009玉溪一中期中)要得到函数的图象,只要将函数的图象 ( ) A.向左平移个单位 B.向左平移个单位 C.向右平移个单位 D.向右平移个单位 9.(2009湛江一模)已知函数,给出下列四个命题: ①若,则 ②的最小正周期是 ③在区间上是增函数 ④的图象关于直线对称 其中真命题是 .①②④ .①③ .②③ .③④ 10.(2009云南师大附中)若函数的取值范围是 A. B. C. D. 二、填空题 1.(2009冠龙高级中学3月月考)已知,则=______________。 2.(2009上海青浦区)把化为积的形式,其结果为 . 3.(2009上海十校联考)函数的单调递增区间是______________. 4.(2009上海重点九校)方程 在区间内的解集 三、解答题 1、(2009广州一模)已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB=. (1)若b=4,求sinA的值; (2) 若△ABC的面积S△ABC=4,求b,c的值. 2.(2009聊城一模)设函数。 (1)写出函数的最小正周期及单调递减区间; (2)当时,函数的最大值与最小值的和为,求的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积。 3.(2009茂名一模)设函数将函数的图象向左平移个单位,得到函数的图象。 (1)求函数的最小正周期; (2)若且是偶函数,求的值。 4.(2009上海八校联考)已知函数. (1)求的最小正周期,并求的最小值; (2)若,且,求的值 5.(2009闵行三中模拟)已知函数是R上的奇函数,且最小正周期为π。 (1)求的值; (2)求取最小值时的x的集合。 6.(2009上海青浦区)已知为实数,函数,(). (1)若,试求的取值范围; (2)若,求函数的最小值. 7.(2009日照一模)已知中,角的对边分别为,且满足。 (I)求角的大小; (Ⅱ)设,求的最小值。 8.(2009汕头一模)己知函数f(x)=sin x一cos x。 (1)若cosx=-,x,求函数f (x)的值; (2)将函数f(x)的图像向右平移m个单位,使平移后的图像关于原点对称, 若0查看更多
相关文章
- 当前文档收益归属上传用户