人教A数学必修一 集合的基本运算

人教A数学必修一 集合的基本运算

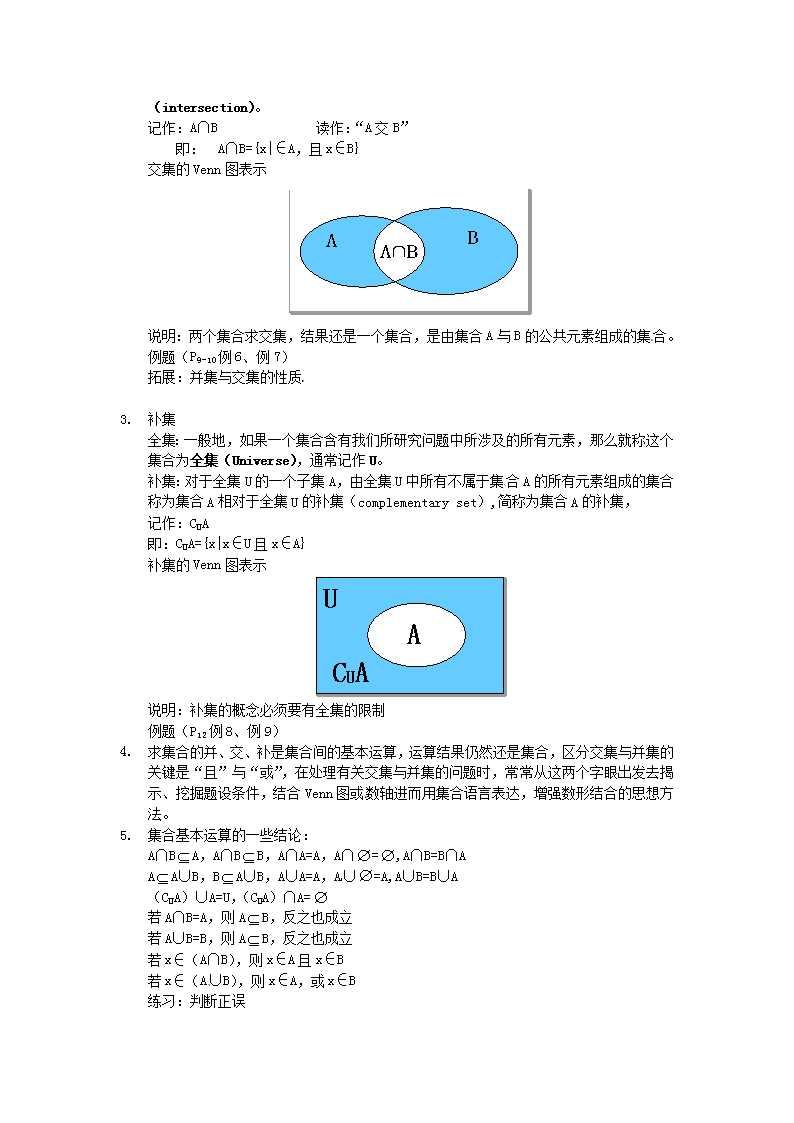
四川省米易中学校高一数学必修一《13 集合的基本运算》教案 教学目的：（1）理解两个集合的并集与交集的的含义，会求两个简单集合的并集与交集；‎ ‎（2）理解在给定集合中一个子集的补集的含义，会求给定子集的补集；（3）能用Venn图表达集合的关系及运算，体会直观图示对理解抽象概念的作用。‎ 课 型：新授课 教学重点：集合的交集与并集、补集的概念； ‎ 教学难点：集合的交集与并集、补集“是什么”，“为什么”，“怎样做”；‎ 教学过程：‎ 一、 引入课题 考察下列各个集合,你能说出集合C与集合A,B之间的关系吗?‎ ‎(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}‎ ‎(2) A={x|x是有理数},B={x|x是无理数},‎ ‎ C={x|x是实数}.‎ 思考（P9思考题），引入并集概念。‎ 二、 新课教学 1. 并集 一般地，由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集（Union）‎ 记作：A∪B 读作：“A并B”‎ 即： A∪B={x|x∈A，或x∈B}‎ ‎ A∪B A B A Venn图表示：‎ ‎?‎ 说明：两个集合求并集，结果还是一个集合，是由集合A与B的所有元素组成的集合（重复元素只看成一个元素）。‎ 例题（P9-10例4、例5）‎ 说明：连续的（用不等式表示的）实数集合可以用数轴上的一段封闭曲线来表示。‎ 问题：在上图中我们除了研究集合A与B的并集外，它们的公共部分（即问号部分）还应是我们所关心的，我们称其为集合A与B的交集。‎ 2. 交集 考察下列各个集合,你能说出集合A,B与集合C之间的关系吗?‎ ‎（1）A={2,4,6,8,10}, B={3,5,8,12} ,C={8};‎ ‎(2) A={x|x是我校在校的女同学},‎ B={x|x是我校的高一级同学},‎ C={x|x是我校的高一级女同学}.‎ 一般地，由属于集合A且属于集合B的元素所组成的集合，叫做集合A与B的交集 ‎（intersection）。‎ 记作：A∩B 读作：“A交B”‎ ‎ 即： A∩B={x|∈A，且x∈B}‎ 交集的Venn图表示 说明：两个集合求交集，结果还是一个集合，是由集合A与B的公共元素组成的集合。‎ 例题（P9-10例6、例7）‎ 拓展：并集与交集的性质 1. 补集 全集：一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，那么就称这个集合为全集（Universe），通常记作U。‎ 补集：对于全集U的一个子集A，由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集（complementary set）,简称为集合A的补集，‎ 记作：CUA 即：CUA={x|x∈U且x∈A}‎ 补集的Venn图表示 说明：补集的概念必须要有全集的限制 例题（P12例8、例9）‎ 2. 求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法。‎ 3. 集合基本运算的一些结论：‎ A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A AA∪B，BA∪B，A∪A=A，A∪=A,A∪B=B∪A ‎（CUA）∪A=U，（CUA）∩A= ‎ 若A∩B=A，则AB，反之也成立 若A∪B=B，则AB，反之也成立 若x∈（A∩B），则x∈A且x∈B 若x∈（A∪B），则x∈A，或x∈B 练习：判断正误 ‎ （1）若U={四边形}，A={梯形}，‎ ‎ 则CUA={平行四边形}‎ ‎ （2）若U是全集，且AÍB，则CUAÍCUB ‎ （3）若U={1，2，3}，A=U，则CUA=f ‎2. 设集合A={|‎2a-1|，2}，B={2，3，a2+‎2a-3}‎ ‎ 且CBA={5}，求实数a的值。‎ ‎3. 已知全集U={1，2，3，4，5}，‎ ‎ 非空集A={xÎU|x2-5x+q=0}，‎ ‎ 求CUA及q的值。‎ 1. 课堂归纳小结（略）‎ 一、 作业布置 1、 书面作业：P13习题1.1，第6-12题