- 2021-06-15 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版数形结合思想的应用情形归纳(4)学案
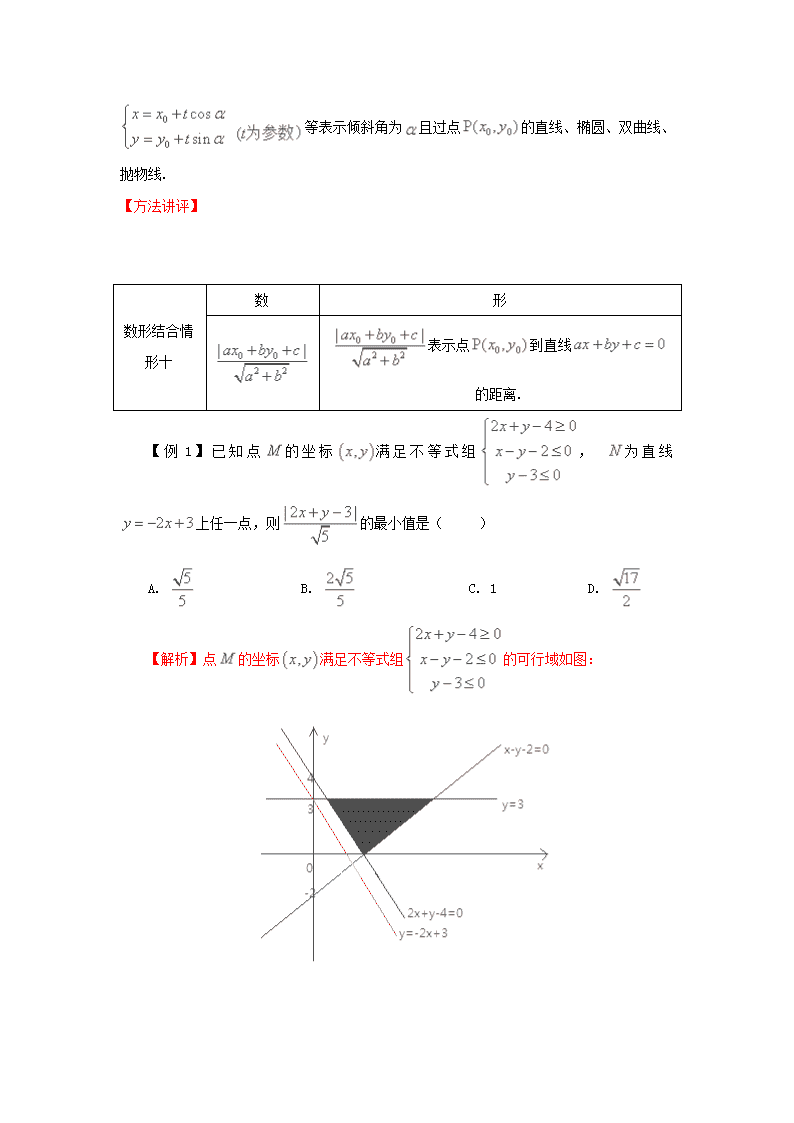
数学思想在高中数学中的应用情形归纳 第03讲:数形结合思想情形之10-13 【知识要点】 一、数学思想是人对数学知识的本质认识,是从某些具体的数学内容和对数学的认识过程中提炼上升的数学观点,它在认识过程中被反复运用,带有普遍的指导意义.是建立数学和用数学解决问题的指导思想,而且数学思想是数学学 的精髓,是数学素养的重要内容之一.学生只有领会了数学思想,才能有效地应用知识,形成能力.在我们解决数学问题进行数学思维时,也总是自觉或不自觉地运用数学思想方法. 高中数学解题常用的数学思想有数形结合思想、分类讨论思想、转化化归思想、函数方程思想等. 二、数形结合,是中学数学最重要的思想方法之一.著名数学家华罗庚先生说:“数与形本是相倚依,怎能分作两边飞,数缺形时少直觉,形少数时难入微,数形结合百般好,隔离分家万事休。切莫忘,几何代数流一体,永远联系切莫分离. ”它精辟地阐述了数形结合的重要性,它不仅是一个重要的数学思想,而且是一种重要的解题方法. 因而数形结合的能力必然是历年高考的一个重点.所谓数形结合的思想方法,就是由数学问题所呈现的条件和结论,通过研究数式的几何意义,或者研究几何问题的代数意义,设法沟通数学问题在数量关系和空间形式的内在联系,使隐含条件明朗化,复杂问题简单化,抽象问题具体化,开拓题目新思路,以便最终找到解决问题的带有数形信息转换特征的数学方法.数形结合思想就是把“数”和它对应的“形”联系起 分析解答数学问题,以形助数,以数解形,数形互助,提高解题效率,优化解题.高中数学中数形结合的情形很多,常见的情形见后面的方法讲评. /- 三、数形结合要注意三个原则:等价性原则、双向性原则、简单性原则. 四、本讲讲了数形结合思想情形之10-13, 情形10:表示点到直线的距离.情形11:方程,表示以点为圆心,以为半 径的圆;情形12:方程等表示椭圆、双曲线、抛物线;情形13:参数方程 等表示倾斜角为且过点的直线、椭圆、双曲线、抛物线. 【方法讲评】 数形结合情形十 数 形 表示点到直线的距离. 【例1】已知点的坐标满足不等式组, 为直线上任一点,则的最小值是( ) A. B. C. 1 D. 【解析】点的坐标满足不等式组的可行域如图: 【点评】(1)本题的关键是找到的几何意义,需要把它转化为,就知道它表示的几何意义了.所以我们在解答数学问题时,要注意观察题目中的数学信息,观察到这一点,问题就迎刃而解了. (2)解答数学问题,要有敏锐的观察力,你能看到别人看不到的信息,你在这方面领先别人了,你离成功便近了一步. 【反馈检测1】已知实数满足,则的最大值与最小值之差为( ) A. B. C. D. 3 数形结合情形十一 数 形 方程,表示以点为圆心,以为半径的圆; 表示以点,以为半径的圆. 【例2】已知圆,直线, . (1) 求证:对,直线与圆总有两个不同的交点A、B; (2) 求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线; (3) 是否存在实数,使得圆C上有四点到直线l的距离为?若存在,求出的范围;若不存在,说明理由. 【解析】(1)圆的圆心为,半径为,所以圆心C到直线的距离.所以直线与圆C相交,即直线与圆总有两个不同的交点. 或:直线的方程可化为,无论m怎么变化,直线过定点,由于,所以点是圆C内一点,故直线与圆总有两个不同的交点. (2)设中点为,因为直线恒过定点, 当直线的斜率存在时, ,又, , 圆心到直线的距离为 化简得,解得或. 【点评】(1)证明直线与圆总有两个不同的交点可以利用判别式法(比较和零的大小关系)、几何法(比较圆心到直线的距离和圆的半径 的大小关系)和定点分析法(找到定点判断定点和圆的位置关系).本题的第1问就是利用了几何法和定点分析法. (2)第2问求轨迹方程用的是直接法,直接把化简即可. (3)第3问用数形结合分析解答比较简洁. 【反馈检测2】在圆上任取一点,点在轴的正射影为点,当点在圆上运动时,动点满足. (Ⅰ)求动点的轨迹;(Ⅱ)如果动点的轨迹为曲线C,.点在曲线上,过点的直线交曲线于两点,设直线斜率为,直线斜率为,求证:为定值. 数形结合情形十二 数 形 ,. 表示焦点在轴上长轴为的椭圆. 表示焦点在轴上长轴为的椭圆. , 表示焦点在轴上实轴为的双曲线. 表示焦点在轴上实轴为的双曲线. 表示焦点在轴上的抛物线. 表示焦点在轴上的抛物线. 【例3】已知, 内切于点是两圆公切线上异于的一点,直线切于点, 切于点,且均不与重合,直线相交于点. (1)求的轨迹;(2)若直线与轴不垂直,它与的另一个交点为, 是点关于轴的对称点,求证:直线过定点. 【解析】(1) 因为内切于于,所以,解得, 所以的方程为: , 因为直线分别切于,所以, 的两个端点). (2)依题意,设直线的方程为, , 则且,联立方程组, 消去,并整理得, , , 直线的方程, 令, 得, 故直线过定点. 【点评】(1)第1问求动点的轨迹用的是定义法(待定系数法),但是要注意除去长轴的两个端点.(2)求直线过定点,一般先求出直线的方程,再找到直线经过的定点. 【反馈检测3】已知动点与双曲线的两个焦点的距离之和为定值,且的最小值为. (1)求动点的轨迹; (2)若已知,在动点的轨迹上且,求实数的取值范围. 数 形 数形结合情形十三 , 表示倾斜角为过点的直线. 表示圆心为半径为的圆. 表示焦点在轴上的椭圆. 表示焦点在轴上的双曲线. 表示焦点在轴上的抛物线. 【例4】在极坐标系中,曲线,曲线.以极点为坐标原点,极轴为轴正半轴建立直角坐标系,曲线的参数方程为(为参数). (1)求的直角坐标方程;学/- (2)与交于不同四点,这四点在上的排列顺次为,求的值. (2) 不妨设四个交点自下而上依次为,它们对应的参数分别为. 把代入, 则, , 所以. 【点评】(1)本题的难点在第2问,解答它的关键是理解直线参数方程中的几何意义.如果不用这种方法,解题就比较复杂. (2)当解析几何中涉及到线段时,都要联想到直线参数方程中的几何意义,看是否能利用参数的几何意义解答. 【反馈检测4】在直角坐标系中,直线的参数方程为(为参数),若以该直角坐标系的原点为极点, 轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为. (Ⅰ)求直线与曲线的普通方程; (Ⅱ)已知直线与曲线交于两点,设,求的值. 数学思想在高中数学教学中的应用情形归纳 第03讲:数形结合思想情形之10-13参考答案 【反馈检测1答案】C 【反馈检测1详细解析】 不等式组对应的区域如图所示,,表示区域内的点到直线的距离,观察得点B(2,-1)到直线的距离最大=,最小距离为0,所以 把,代入方程①,得, 所以动点M的轨迹方程为,它是焦点在x轴上,长轴为4的椭圆. / - (Ⅱ)方法一:由题意知直线斜率不为0,设直线方程为, 由消去,得, 易知,得 .所以为定值 方法二:(ⅰ)当直线斜率不存在时, .所以为定值 【反馈检测3答案】(1),它表示焦点在x轴上,长轴为6的椭圆;(2). 【反馈检测3详细解析】(1)由题意.设(),由余弦定理, 得 又·,当且仅当时,取最大值, 此时取最小值,令, 解得,,∴,故所求的轨迹方程为. 它表示焦点在x轴上,长轴为6的椭圆. (2)设,,则由,可得 =, 故,. ∵在动点的轨迹上,且, 消去可得,解得, 又,∴,解得,故实数的取值范围是. 【反馈检测4答案】(Ⅰ); ,(Ⅱ) . 【反馈检测4详细解析】(Ⅰ)由得, ∴直线的普通方程; 由得, 又∵, ∴曲线的普通方程为.查看更多