【数学】2019届一轮复习北师大版函数、不等式中恒成立问题学案
纵观近几年高考对于函数、不等式中恒成立问题的考查,重点是涉及到一次函数、二次函数的性质、不等式的性质及应用,图象渗透和换元、化归、数形结合、函数与方程、分类讨论、转化等数学思想方法.往往与导数相结合,在处理复杂问题时转化成为“恒成立问题”.解答这类题目应首先克服畏惧心理,通过总结高中阶段出现的这类问题的类型,形成完整的知识、方法体系,提高应对能力.
一. 函数性质法
1.一次函数
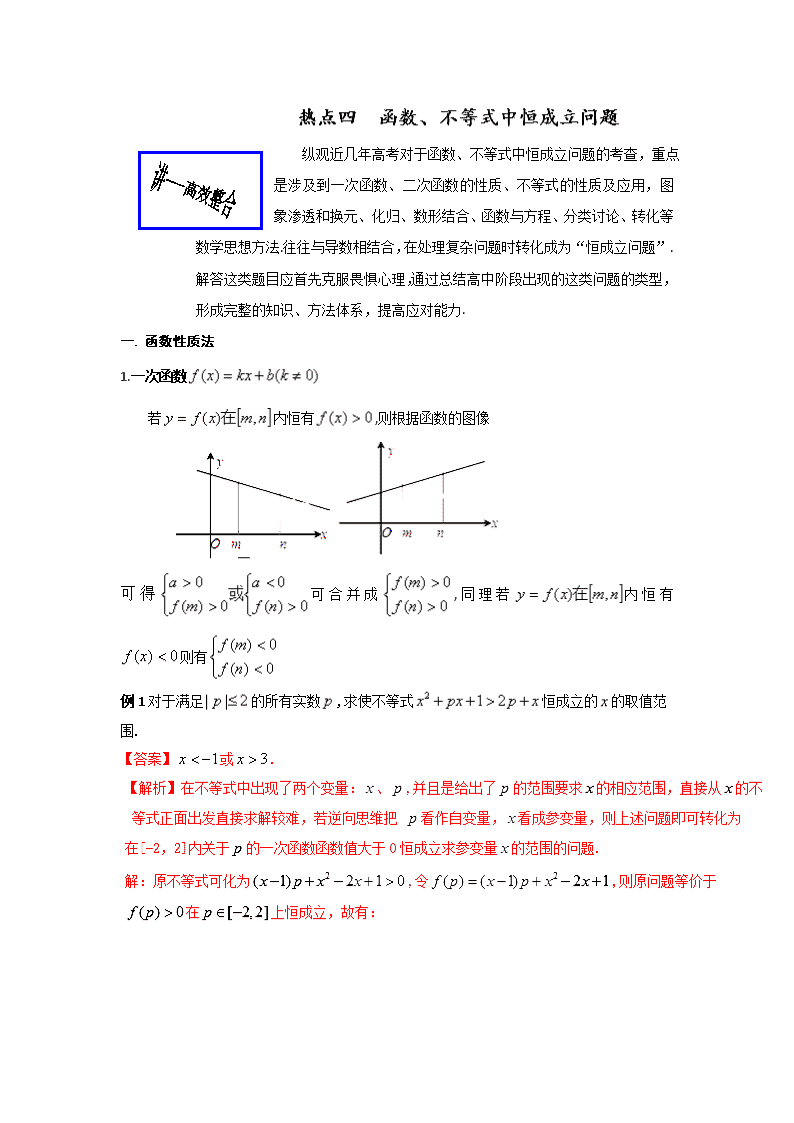
若内恒有,则根据函数的图像
可得可合并成,同理若内恒有则有
例1对于满足的所有实数,求使不等式恒成立的的取值范围.
【答案】或.
o
y
2
-2
x
y
-2
2 x
2. 二次函数——利用判别式、韦达定理及根的分布求解
有以下几种基本类型
类型1 设
(1) 上恒成立;
(2)上恒成立.
类型2 设
(1)当时,上恒成立
上恒成立
(2)当时,上恒成立
上恒成立
例2【2018届内蒙古包钢第一中学高三上第一次月考】若不等式对一切实数恒成立,则关于的不等式的解集为 学
A. B.
C. D.
【答案】B
【解析】对一切实数恒成立,所以,
所以0
4x+m-3恒成立,则x的取值范围是________________.
【答案】(-∞,-1)∪(3,+∞)
四. 数形结合
若所给不等式进行合理的变形化为(或)后,能非常容易地画出不等号两边函数的图像,则可以通过画图直接判断得出结果.尤其对于选择题、填空题这种方法更显方便、快捷.
例7.求证 ,对于恒有成立.
【答案】.
【解析】原方程可化为,由图像可知,,函数单调递增
,故得证.
五. 消元转化法
例8.已知是定义在上的奇函数,且,若,若[ 学_ _ ]
对于所有的恒成立,求实数t的取值范围.学
【答案】
六. 应用导数研究恒成立问题
通过导数证明不等式或研究不等式恒成立问题的基本思路是 以导函数和不等式为基础,单调性为主线,最(极)值为助手,利用转化与化归思想,从数形结合、分类讨论等多视角进行探究,经常是把不等式问题转化为判断函数的单调性、求函数的最值,利用最值得出相应结论,其中分类讨论是经常用到的数学思想方法.
例9【2018届皖江名校高三12月份大联考】已知函数(其中)在点处的切线斜率为1.
(1)用表示;
(2)设,若对定义域内的恒成立,求实数的取值范围;
(3)在(2)的前提下,如果,证明 .
【答案】(1);(2);(III)证明见解析.
【解析】试题分析 (1)由题意即得;
(2)在定义域上恒成立,即,由恒成立,得,再证当时, 即可;
(3)由(2)知,且在单调递减;在单调递增,当时,不妨设,要证明,等价于,需要证明
,令,可证得在上单调递增, 即可证得.
对恒成立,
令,则。学
这里先证明,记,则,
易得在上单调递增,在上单调递减, ,所以。
因此, ,且时,
所以,实数的取值范围是。
(3)由(2)知,且在单调递减;在单调递增,
当时,不妨设,要证明,等价于,
只需要证明,这里,
【反思提升】上述例子剖析了数学高考中恒成立问题的常见题型及解法,解决这类题目要看清式子的特征,选择合适的方法,以便事半功倍.(1)对于含二次项恒成立的问题,注意讨论二次项系数是否为0,这是容易漏掉的地方.(2)恒成立问题一般需转化为最值,利用单调性证明在闭区间的单调性.(3)一元二次不等式在上恒成立,看开口方向和判别式.(4)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法 一是利用二次函数在区间上的最值 处理;二是分离参数,再去求函数的最值 处理,一般后者比较简单.(5)值得一提的是,各种类型各种方法并不是完全孤立的,虽然方法表现的形式不尽相同,但其实质却往往与求函数的最值息息相关,从而在解数学函数与不等式恒成立的过程中,欣赏一下数学中的“统一美”,在努力攀登知识的高峰中,不要忘了多看身边的美景,度过有意义的时光.