- 2021-05-14 发布 |
- 37.5 KB |
- 4页


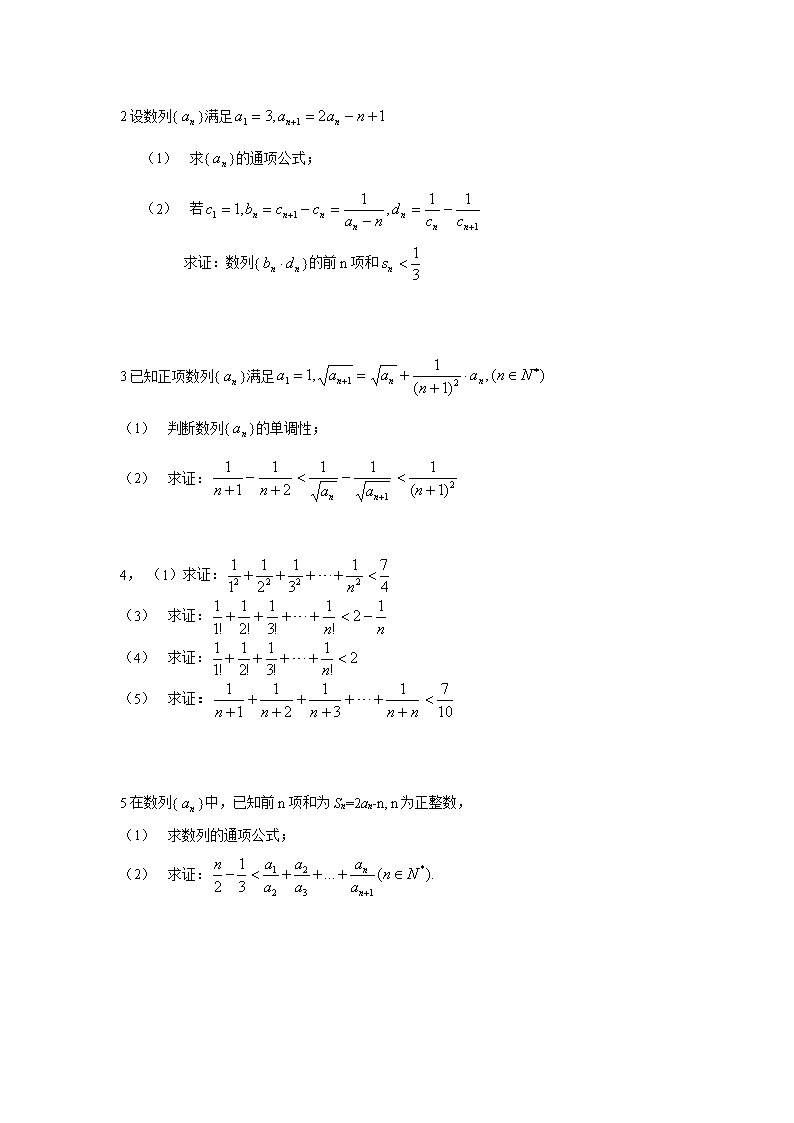
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考专题放缩法竞赛辅导
专题—放缩法证明数列不等式 放缩法是不等式证明中一种常用的方法,也是一种非常重要的方法。在证明过程中,适当地进行放缩,可以化繁为简、化难为易,达到事半功倍的效果。但放缩的范围较难把握,常常出现放缩之后得不出结论或得出相反结论的现象。因此,使用放缩法时,如何确定放缩目标尤为重要。要想正确确定放缩目标,就必须根据欲证结论,抓住题目的特点。掌握放缩技巧,真正做到弄懂弄通,并且还要根据不同题目的类型,采用恰到好处的放缩方法,才能把题解活,从而培养和提高自己的思维和逻辑推理能力,分析问题和解决问题的能力。 数列与不等式的综合问题常常出现在高考的压轴题中,是历年高考命题的热点,这类问题能有效地考查学生综合运用数列与不等式知识解决问题的能力.本文介绍一类与数列和有关的不等式问题,解决这类问题常常用到放缩法,而求解途径一般有两条:一是先求和再放缩,二是先放缩再求和. 注:常用放缩的结论:(1) (2). 例1.正数数列的前项的和,满足,试求: (1)数列的通项公式; (2)设,数列的前项的和为,求证: 例2.已知各项均为正数的数列的前项和为,且. (1) 求证:; (2) 求证: 例3.(1)设a,n∈N*,a≥2,证明:; (2)等比数列{an}中,,前n项的和为An,且A7,A9,A8成等差数列.设,数列{bn}前n项的和为Bn,证明:Bn<. 例4.已知数列满足:,.求证: 例5.在m(m≥2)个不同数的排列P1P2…Pn中,若1≤i<j≤m时Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列的逆序数为an,如排列21的逆序数,排列4321的逆序数. (1)求a4、a5,并写出an的表达式; (2)令,证明,n=1,2,…. 练习1已知数列{a}满足:a=1且. (1) 求数列{a}的通项公式; (2) 设mN,mn2,证明(a+)(m-n+1) 2设数列{}满足 (1) 求{}的通项公式; (2) 若 求证:数列{}的前n项和 3已知正项数列{}满足 (1) 判断数列{}的单调性; (2) 求证: 4, (1)求证: (3) 求证: (4) 求证: (5) 求证: 5在数列{}中,已知前n项和为Sn=2an-n, n为正整数, (1) 求数列的通项公式; (2) 求证: 6 已知数列{an}的前n项和Sn满足:Sn=2an +(-1)n,n≥1. (Ⅰ)写出求数列{an}的前3项a1,a2,a3; (Ⅱ)求数列{an}的通项公式; (Ⅲ)证明:对任意的整数m>4,有. 7,设等比数列的前n项和为,已知对,点均在函数 ()的图像上, (1) 求 r的值; (2) 当 b=2 时,记,求证对,不等式 成立。 8,对于任意大于1的自然数n,证明: 9,已知曲线,,从点P(-1,0)向曲线引斜率为的切线,切点为 (1)求数列的通项公式。 (2)证明查看更多