- 2021-05-14 发布 |
- 37.5 KB |
- 8页


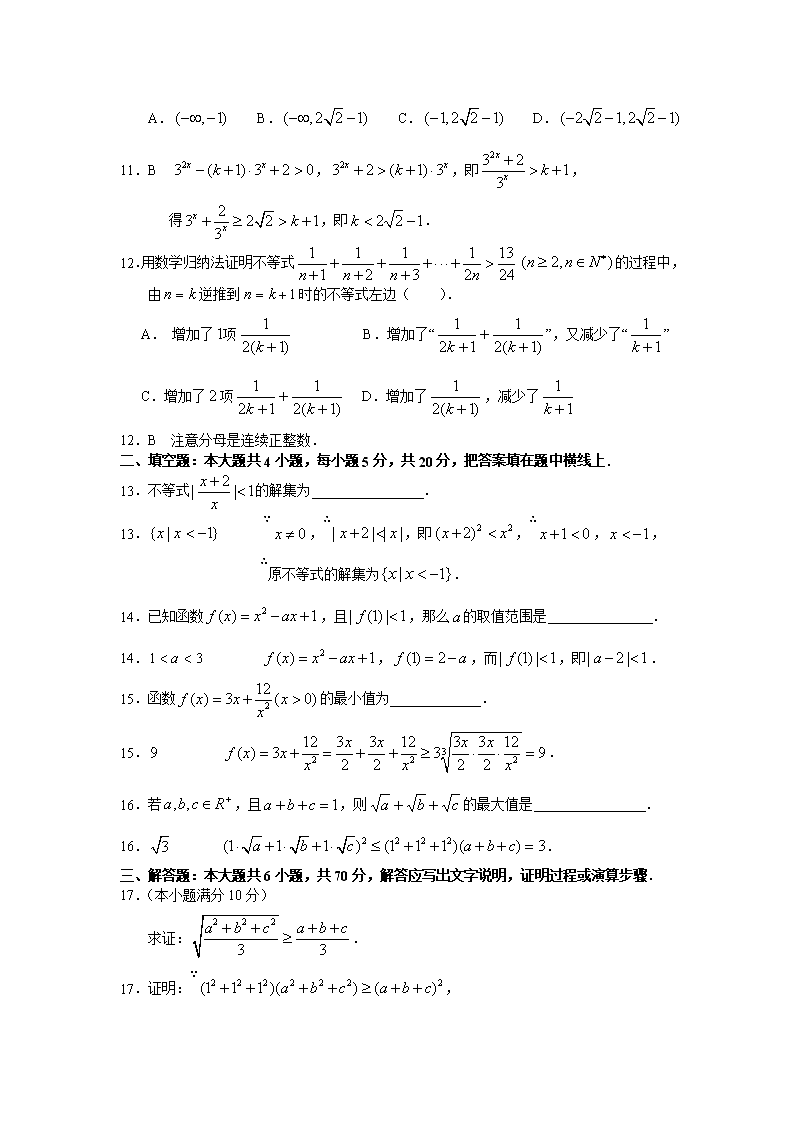
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
选修不等式选讲高考真题训练
不等式选讲综合测试 海南 李传牛 一、选择题:本大题共12小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的. 1.若,则下列不等式中正确的是( ). A. B. C. D. 1.D . 2.设, ,则的大小关系是( ). A. B. C. D. 2.B ,即. 通过放大分母使得分母一样,整个分式值变小 3.设命题甲:,命题乙:,则甲是乙的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3. A 命题甲:,或,甲可推出乙. 4.已知为非零实数,则最小值为( ) . A. B. C. D. 4.B , ∴所求最小值为. 5.正数满足,,则有( ). A. B. C. D.与大小不定 5.C 特殊值:正数,满足,得. 或由得, ∴,(1) 由得,(2) 将(1)代入(2)得,即,∴. 6.如果关于的不等式的非负整数解是,那么实数的取值 范围是( ). A. B. C. D. 6.A ,得,而正整数解是,则. 7.设,则的最小值为( ). A. B. C. D. 7.C , . 8.已知的解集与的解集相同,则( ). A. B. C. D. 8.B 由解得,因为的解集与 的解集相同,那么或为方程的解,则分别代入该方程,得. 9.已知不等式对任意正实数恒成立,则正实数的最小值为( ). A. B. C. D. 9.B ∵,∴,∴. 10.设,则的最大值为( ). A. B. C. D. 10.C 由排序不等式,所以. 11.已知,当时,恒为正,则的取值范围是( ). A. B. C. D. 11.B ,,即, 得,即. 12.用数学归纳法证明不等式的过程中,由逆推到时的不等式左边( ). A. 增加了项 B.增加了“”,又减少了“” C.增加了项 D.增加了,减少了 12.B 注意分母是连续正整数. 二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上. 13.不等式的解集为 . 13. ∵,∴,即,∴,, ∴原不等式的解集为. 14.已知函数,且,那么的取值范围是 . 14. ,,而,即. 15.函数的最小值为_____________. 15. . 16.若,且,则的最大值是 . 16. . 三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) 求证:. 17.证明:∵, ∴, 即. 18.(本小题满分10分) 无论取任何非零实数,试证明等式总不成立. 18.证明:设存在非零实数,使得等式成立, 则, ∴,即, 但是,即,从而得出矛盾. 故原命题成立. 19.(本小题满分12分) 已知,,为的三边,求证:. 19.证明:由余弦定理得,, , 三式相加得, 而,且三者至多一个可等于, 即, 所以. 20.(本小题满分12分) 已知都是正数,求证:. 20.证明:要证, 只需证,即, 移项得, ∵都是正数, ∴, ∴原不等式成立. 21.(本小题满分12分) 某单位决定投资元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价元,两侧墙砌砖,每米造价元,顶部每平方米造价元,试问:(1)仓库面积的最大允许值是多少?(2)为使达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长? 21.解:如图,设铁栅长为米,一堵砖墙长为米,则有, 由题意得, 应用二元均值不等式, 得 ∴,即, ∵,∴,∴. 因此,的最大允许值是平方米,取得此最大值的条件是, 而,求得,即铁栅的长应是米. 22.(本小题满分12分) 已知是定义在上的单调递增函数,对于任意的满足 ,且,满足. (1)求; (2)若,解不等式; (3)求证:. 22.解:(1)因为任意的满足, 令,则,得; (2), 而, 得,而是定义在上的单调递增函数, ,得不等式的解集为; (3)∵,在上的单调递增, ∴时,,时,. 又,或, ∵,则,∴, ∴, ∴,得. ∵,且,,, ∴,∴, 得,∴, 即,而, ∴,又, ∴. 答案与解析: 备用题: 1.已知,,则下列命题中正确的是( ). A. B. C. D. 1.D 令,可验证知D成立, 事实上我们有①,②,①﹢②可得. 2.已知,.设命题甲:满足;命题乙:且,那么甲是乙的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分条件也不必要条件 2.B ,,则,而, 即;命题甲:不能推出命题乙:且. 3.证明 ,假设时成立,当时,左端增加的项数是( ). A.项 B.项 C.项 D.项 3.D 从增加的项数是. 4.如果恒成立,则的取值范围是 . 4. ,而恒成立,则,即. 5.已知函数在区间上的最大值比最小值大,则实数 . 5. 显然,而,则, 得是函数的递减区间, ,, 即,得, ,而,则. 6.要制作如图所示的铝合金窗架,当窗户采光面积为 一常数时(中间横梁面积忽略不计),要使所用的铝合 金材料最省,窗户的宽与高的比应为 . 6. 设宽为,高为,则,所用的铝合金材料为, ,此时,. 7.若,试比较与的大小. 7.解:, 即,而,则, 得,即,所以. 8.已知,设:函数在上单调递减,:不等式的解集 为.如果和有且仅有一个正确,求的取值范围. 8.解:∵在上单调递减,∴, 又∵的最小值是, ∴,即, 由题设,当为真为假时,有,且, ∴; 当为假为真时,有且,∴. 故的取值范围是. 作 者 李传牛 工作单位 海南省海口市第十四中学 邮政编码 570311 联系手机 13976611338 E--MAIL lcn111@sohu.com QQ交流 284682392查看更多