河北省邯郸市高考数学模拟试卷理科解析

河北省邯郸市高考数学模拟试卷理科解析

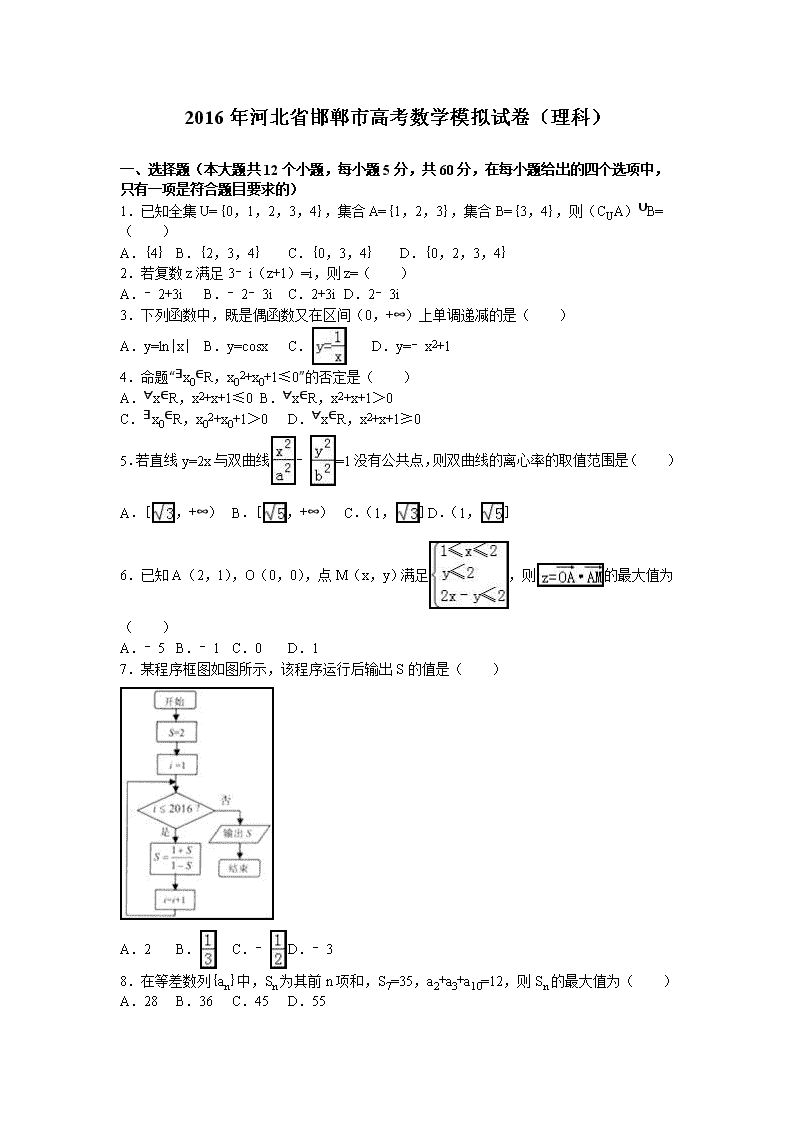
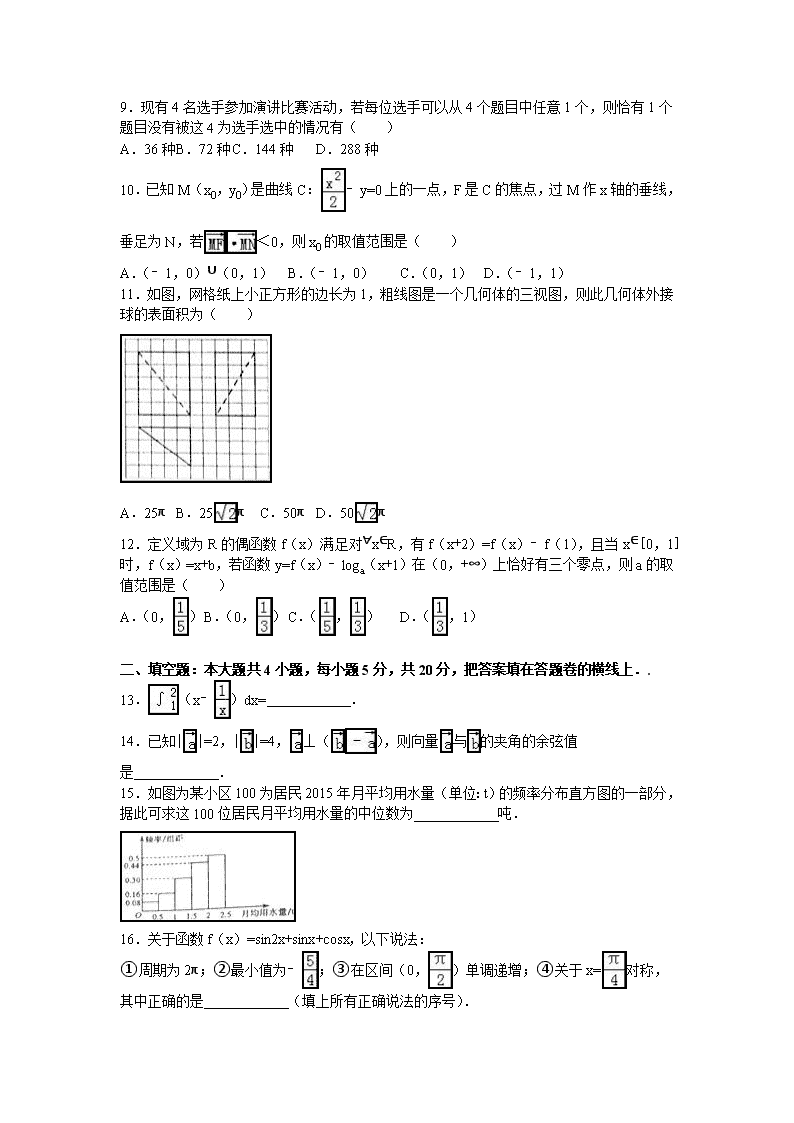
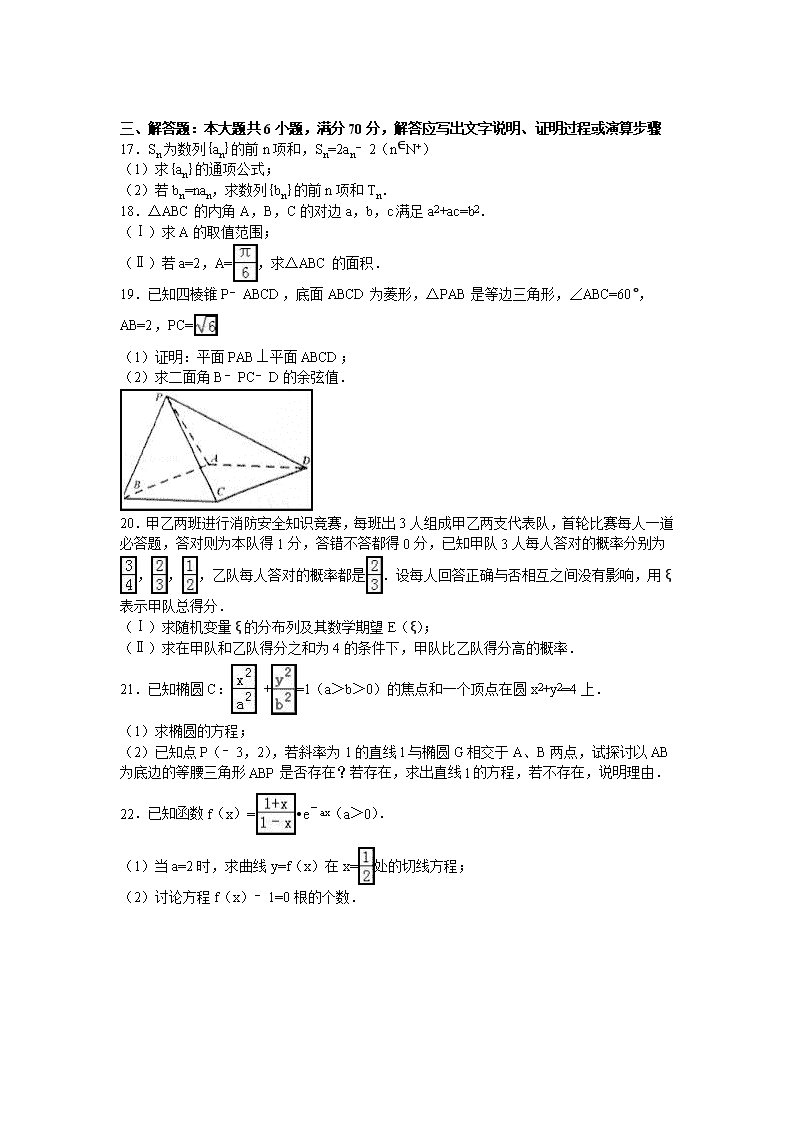
‎2016年河北省邯郸市高考数学模拟试卷（理科）‎ ‎　‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，集合B={3，4}，则（CUA）∪B=（　　）‎ A．{4} B．{2，3，4} C．{0，3，4} D．{0，2，3，4}‎ ‎2．若复数z满足3﹣i（z+1）=i，则z=（　　）‎ A．﹣2+3i B．﹣2﹣3i C．2+3i D．2﹣3i ‎3．下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（　　）‎ A．y=ln|x| B．y=cosx C． D．y=﹣x2+1‎ ‎4．命题“∃x0∈R，x02+x0+1≤0”的否定是（　　）‎ A．∀x∈R，x2+x+1≤0 B．∀x∈R，x2+x+1＞0‎ C．∃x0∈R，x02+x0+1＞0 D．∀x∈R，x2+x+1≥0‎ ‎5．若直线y=2x与双曲线﹣=1没有公共点，则双曲线的离心率的取值范围是（　　）‎ A．[，+∞） B．[，+∞） C．（1，] D．（1，]‎ ‎6．已知A（2，1），O（0，0），点M（x，y）满足，则的最大值为（　　）‎ A．﹣5 B．﹣1 C．0 D．1‎ ‎7．某程序框图如图所示，该程序运行后输出S的值是（　　）‎ A．2 B． C．﹣ D．﹣3‎ ‎8．在等差数列{an}中，Sn为其前n项和，S7=35，a2+a3+a10=12，则Sn的最大值为（　　）‎ A．28 B．36 C．45 D．55‎ ‎9．现有4名选手参加演讲比赛活动，若每位选手可以从4个题目中任意1个，则恰有1个题目没有被这4为选手选中的情况有（　　）‎ A．36种 B．72种 C．144种 D．288种 ‎10．已知M（x0，y0）是曲线C：﹣y=0上的一点，F是C的焦点，过M作x轴的垂线，垂足为N，若＜0，则x0的取值范围是（　　）‎ A．（﹣1，0）∪（0，1） B．（﹣1，0） C．（0，1） D．（﹣1，1）‎ ‎11．如图，网格纸上小正方形的边长为1，粗线图是一个几何体的三视图，则此几何体外接球的表面积为（　　）‎ A．25π B．25π C．50π D．50π ‎12．定义域为R的偶函数f（x）满足对∀x∈R，有f（x+2）=f（x）﹣f（1），且当x∈[0，1]时，f（x）=x+b，若函数y=f（x）﹣loga（x+1）在（0，+∞）上恰好有三个零点，则a的取值范围是（　　）‎ A．（0，） B．（0，） C．（，） D．（，1）‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．.‎ ‎13．（x﹣）dx=　　　　　　．‎ ‎14．已知||=2，||=4，⊥（），则向量与的夹角的余弦值是　　　　　　．‎ ‎15．如图为某小区100为居民2015年月平均用水量（单位：t）的频率分布直方图的一部分，据此可求这100位居民月平均用水量的中位数为　　　　　　吨．‎ ‎16．关于函数f（x）=sin2x+sinx+cosx，以下说法：‎ ‎①周期为2π；②最小值为﹣；③在区间（0，）单调递增；④关于x=对称，‎ 其中正确的是　　　　　　（填上所有正确说法的序号）．‎ ‎　‎ 三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤 ‎17．Sn为数列{an}的前n项和，Sn=2an﹣2（n∈N+）‎ ‎（1）求{an}的通项公式；‎ ‎（2）若bn=nan，求数列{bn}的前n项和Tn．‎ ‎18．△ABC的内角A，B，C的对边a，b，c满足a2+ac=b2．‎ ‎（Ⅰ）求A的取值范围；‎ ‎（Ⅱ）若a=2，A=，求△ABC的面积．‎ ‎19．已知四棱锥P﹣ABCD，底面ABCD为菱形，△PAB是等边三角形，∠ABC=60°，AB=2，PC=‎ ‎（1）证明：平面PAB⊥平面ABCD；‎ ‎（2）求二面角B﹣PC﹣D的余弦值．‎ ‎20．甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为，，，乙队每人答对的概率都是．设每人回答正确与否相互之间没有影响，用ξ表示甲队总得分．‎ ‎（Ⅰ）求随机变量ξ的分布列及其数学期望E（ξ）；‎ ‎（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．‎ ‎21．已知椭圆C： +=1（a＞b＞0）的焦点和一个顶点在圆x2+y2=4上．‎ ‎（1）求椭圆的方程；‎ ‎（2）已知点P（﹣3，2），若斜率为1的直线l与椭圆G相交于A、B两点，试探讨以AB为底边的等腰三角形ABP是否存在？若存在，求出直线l的方程，若不存在，说明理由．‎ ‎22．已知函数f（x）=•e﹣ax（a＞0）．‎ ‎（1）当a=2时，求曲线y=f（x）在x=处的切线方程；‎ ‎（2）讨论方程f（x）﹣1=0根的个数．‎ ‎　‎ ‎2016年河北省邯郸市高考数学模拟试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，集合B={3，4}，则（CUA）∪B=（　　）‎ A．{4} B．{2，3，4} C．{0，3，4} D．{0，2，3，4}‎ ‎【考点】交、并、补集的混合运算．‎ ‎【分析】根据全集、补集与并集的定义，进行计算即可．‎ ‎【解答】解：全集U={0，1，2，3，4}，集合A={1，2，3}，集合B={3，4}，‎ ‎∴CUA={0，4}，‎ ‎∴（CUA）∪B={0，3，4}．‎ 故选：C．‎ ‎　‎ ‎2．若复数z满足3﹣i（z+1）=i，则z=（　　）‎ A．﹣2+3i B．﹣2﹣3i C．2+3i D．2﹣3i ‎【考点】复数代数形式的乘除运算．‎ ‎【分析】把已知等式变形，和利用复数代数形式的乘除运算化简得答案．‎ ‎【解答】解：由3﹣i（z+1）=i，得 i（z+1）=3﹣i，‎ ‎∴z+1=，‎ 则z=﹣2﹣3i．‎ 故选：B．‎ ‎　‎ ‎3．下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（　　）‎ A．y=ln|x| B．y=cosx C． D．y=﹣x2+1‎ ‎【考点】奇偶性与单调性的综合．‎ ‎【分析】根据函数奇偶性和单调性的性质分别进行判断即可．‎ ‎【解答】解：y=ln|x|是偶函数，则（0，+∞）上单调递增，不满足条件．‎ y=cosx是偶函数，则（0，+∞）上不单调，不满足条件．‎ 是奇函数，则（0，+∞）上单调递减，不满足条件．‎ y=﹣x2+1是偶函数，则（0，+∞）上单调递减，满足条件．‎ 故选：D ‎　‎ ‎4．命题“∃x0∈R，x02+x0+1≤0”的否定是（　　）‎ A．∀x∈R，x2+x+1≤0 B．∀x∈R，x2+x+1＞0‎ C．∃x0∈R，x02+x0+1＞0 D．∀x∈R，x2+x+1≥0‎ ‎【考点】命题的否定．‎ ‎【分析】特称命题“∃x0∈R，x02+x0+1≤0”的否定是：把∃改为∀，其它条件不变，然后否定结论，变为一个全称命题．即“∀x∈R，x2+x+1＞0”．‎ ‎【解答】解：特称命题“∃x0∈R，x02+x0+1≤0”的否定是全称命题：‎ ‎“∀x∈R，x2+x+1＞0”．‎ 故选B．‎ ‎　‎ ‎5．若直线y=2x与双曲线﹣=1没有公共点，则双曲线的离心率的取值范围是（　　）‎ A．[，+∞） B．[，+∞） C．（1，] D．（1，]‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】求出双曲线的渐近线方程，由题意可得渐近线的斜率的正值不大于2，由a，b，c的关系和离心率公式，可得范围．‎ ‎【解答】解：双曲线的渐近线方程为y=±x，‎ 由直线y=2x与双曲线﹣=1没有公共点，‎ 可得≤2，即b≤2a，‎ 又e==≤=，‎ 但e＞1，可得1＜e≤．‎ 故选：D．‎ ‎　‎ ‎6．已知A（2，1），O（0，0），点M（x，y）满足，则的最大值为（　　）‎ A．﹣5 B．﹣1 C．0 D．1‎ ‎【考点】简单线性规划．‎ ‎【分析】先画出平面区域D，进行数量积的运算即得z=2x+y﹣5，所以y=﹣2x+5+z，所以根据线性规划的方法求出z的最大值即可．‎ ‎【解答】解：表示的平面区域D，如图中阴影部分所示，‎ 的=（2，1）•（x﹣2，y﹣1）=2x+y﹣5；‎ ‎∴y=﹣2x+5+z；‎ ‎∴5+z表示直线y=﹣2x+5+z在y轴上的截距，所以截距最大时z最大；‎ 如图所示，当该直线经过点A（2，2）时，截距最大，此时z最大；‎ 所以点（2，2）带人直线y=﹣2x+5+z即得z=1．‎ 故选：D．‎ ‎　‎ ‎7．某程序框图如图所示，该程序运行后输出S的值是（　　）‎ A．2 B． C．﹣ D．﹣3‎ ‎【考点】程序框图．‎ ‎【分析】模拟执行程序，依次写出每次循环得到的S，i的值，当i=2017时不满足条件i≤2016，退出循环，输出S的值，即可得解．‎ ‎【解答】解：模拟执行程序，可得 S=2，i=1‎ 满足条件i≤2016，S=﹣3，i=2‎ 满足条件i≤2016，S=﹣，i=3‎ 满足条件i≤2016，S=，i=4‎ 满足条件i≤2016，S=2，i=5‎ ‎…‎ 观察规律可知S的取值周期为4，由2016=504×4可得 满足条件i≤2016，S=，i=2016‎ 满足条件i≤2016，S=2，i=2017‎ 不满足条件i≤2016，退出循环，输出S的值为2．‎ 故选：A．‎ ‎　‎ ‎8．在等差数列{an}中，Sn为其前n项和，S7=35，a2+a3+a10=12，则Sn的最大值为（　　）‎ A．28 B．36 C．45 D．55‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】由题意和等差数列的求和公式和性质可得a4=5，a5=4，进而可得通项公式，可得数列前8项为正数，第9项为0，从第10项开始为负数，可得结论．‎ ‎【解答】解：∵在等差数列{an}中，Sn为其前n项和，S7=35，a2+a3+a10=12，‎ ‎∴S7=7a4=35，a2+a3+a10=3a5=12，∴a4=5，a5=4，‎ ‎∴公差d=a5﹣a4=﹣1，故an=5﹣（n﹣4）=9﹣n，‎ 故数列的前8项为正数，第9项为0，从第10项开始为负数，‎ 故数列的前8或9项和最大为S9=9a5=36，‎ 故选：B．‎ ‎　‎ ‎9．现有4名选手参加演讲比赛活动，若每位选手可以从4个题目中任意1个，则恰有1个题目没有被这4为选手选中的情况有（　　）‎ A．36种 B．72种 C．144种 D．288种 ‎【考点】计数原理的应用．‎ ‎【分析】利用间接法，先确定4个选手无遗漏的选择，再去掉恰好2、3、4道题目被选的情况，即可得出结论．‎ ‎【解答】解：由题意，每个选手都有4种选择，所以4个选手无遗漏的选择是44种，‎ 其中恰好2道题目被选的有C42（C43A22+C42）=84、恰好3道未被选（四人选了同一题目，有4种）、恰好0道题未被选的（4个题目都被选，有A44=24种）．‎ 故共有256﹣84﹣4﹣24=144种．‎ 故选：C．‎ ‎　‎ ‎10．已知M（x0，y0）是曲线C：﹣y=0上的一点，F是C的焦点，过M作x轴的垂线，垂足为N，若＜0，则x0的取值范围是（　　）‎ A．（﹣1，0）∪（0，1） B．（﹣1，0） C．（0，1） D．（﹣1，1）‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】由题意可设M（x0，），（x0≠0），求得N的坐标，求出抛物线的焦点坐标，运用向量的数量积的坐标表示，解不等式即可得到所求范围．‎ ‎【解答】解：由题意可设M（x0，），（x0≠0），‎ 由题意可得N（x0，0），‎ 又抛物线x2=2y的焦点F（0，），‎ 即有=（﹣x0，﹣），=（0，﹣），‎ 由＜0，即为（﹣）•（﹣）＜0，‎ 即有x02＜1且x0≠0），‎ 解得﹣1＜x0＜0且0＜x0＜1．‎ 故选：A．‎ ‎　‎ ‎11．如图，网格纸上小正方形的边长为1，粗线图是一个几何体的三视图，则此几何体外接球的表面积为（　　）‎ A．25π B．25π C．50π D．50π ‎【考点】球内接多面体；简单空间图形的三视图．‎ ‎【分析】几何体是底面为直角三角形的直三棱柱，补充为长方体，长宽高分别为3，4，5，求出对角线长，可得外接球的半径，代入球的表面积公式计算．‎ ‎【解答】解：由三视图知：几何体是底面为直角三角形的直三棱柱，补充为长方体，长宽高分别为3，4，5，‎ 其对角线长为=5，‎ ‎∴此几何体外接球的半径为 ‎∴外接球的表面积S=4π×（）2=50π．‎ 故选：C．‎ ‎　‎ ‎12．定义域为R的偶函数f（x）满足对∀x∈R，有f（x+2）=f（x）﹣f（1），且当x∈[0，1]时，f（x）=x+b，若函数y=f（x）﹣loga（x+1）在（0，+∞）上恰好有三个零点，则a的取值范围是（　　）‎ A．（0，） B．（0，） C．（，） D．（，1）‎ ‎【考点】函数零点的判定定理．‎ ‎【分析】根据条件先求出f（1）=0，即函数f（x）是周期为2的周期函数，然后根据奇偶性求出函数在一个周期内的图象，结合函数与方程之间的关系转化两个函数的交点个数问题，利用数形结合建立不等式关系进行求解即可．‎ ‎【解答】解：∵偶函数f（x）满足对∀x∈R，有f（x+2）=f（x）﹣f（1），‎ ‎∴令x=﹣1，得f（﹣1+2）=f（﹣1）﹣f（1），‎ 即f（1）=f（1）﹣f（1）=0，‎ 则f（1）=0，‎ 即对∀x∈R，有f（x+2）=f（x）﹣f（1）=f（x），‎ 则函数f（x）是周期为2的周期函数，‎ ‎∵当x∈[0，1]时，f（x）=x+b，‎ ‎∴f（1）=1+b=0，则b=﹣1，‎ 即当x∈[0，1]时，f（x）=x﹣1，‎ 若x∈[﹣1，0]时，﹣x∈[0，1]时，‎ 则f（﹣x）=﹣x﹣1=f（x），‎ 则当x∈[﹣1，0]时，f（x）=x+1，‎ 由函数y=f（x）﹣loga（x+1）=0，得f（x）=loga（x+1），‎ 作出f（x）和g（x）=loga（x+1）在（0，+∞）上的图象 若函数y=f（x）﹣loga（x+1）在（0，+∞）上恰好有三个零点，‎ 则等价为两个函数f（x）和g（x）在（0，+∞）上恰好有三个交点，‎ 若a＞1，两个函数只有一个交点，不满足条件．‎ 若0＜a＜1，要使两个函数有三个交点，‎ 则点A（2，﹣1）则g（x）的图象的下方，B（4，﹣1）在g（x）的上方，‎ 即，即，即＜a＜，‎ 即实数a的取值范围是（，），‎ 故选：C ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．.‎ ‎13．（x﹣）dx=　1﹣ln2　．‎ ‎【考点】定积分．‎ ‎【分析】根据：积分公式化简求解∫（x﹣）dx=（x﹣lnx）|，利用牛顿莱布尼兹定理得出答案即可．‎ ‎【解答】解：∫（x﹣）dx=（x﹣lnx）|=2﹣ln2﹣1+ln1=1﹣ln2，‎ 故答案为：1﹣ln2‎ ‎　‎ ‎14．已知||=2，||=4，⊥（），则向量与的夹角的余弦值是　　．‎ ‎【考点】平面向量数量积的运算．‎ ‎【分析】由便可得出，进行数量积的运算便可得到，从而便可得出向量与夹角的余弦值．‎ ‎【解答】解：∵；‎ ‎∴；‎ 即=；‎ ‎∴；‎ 即向量与夹角的余弦值是．‎ 故答案为：．‎ ‎　‎ ‎15．如图为某小区100为居民2015年月平均用水量（单位：t）的频率分布直方图的一部分，据此可求这100位居民月平均用水量的中位数为　2.02　吨．‎ ‎【考点】频率分布直方图．‎ ‎【分析】根据频率分布直方图，求出使直方图中左右两边频率相等对应的横坐标的值．‎ ‎【解答】解：根据频率分布直方图，得；‎ ‎0.08×0.5+0.16×0.5+0.30×0.5+0.44×0.5=0.49＜0.5，‎ ‎0.49+0.5×0.5=0.74＞0.5，‎ 设中位数为a，则 ‎0.49+（a﹣2）×0.5=0.5，‎ 解得a=2.02，‎ ‎∴估计中位数是2.02．‎ 故答案为：2.02．‎ ‎　‎ ‎16．关于函数f（x）=sin2x+sinx+cosx，以下说法：‎ ‎①周期为2π；②最小值为﹣；③在区间（0，）单调递增；④关于x=对称，‎ 其中正确的是　①②④　（填上所有正确说法的序号）．‎ ‎【考点】三角函数的化简求值．‎ ‎【分析】①由f（x+2π）=f（x）即可得证；‎ ‎②换元法，设t=sinx+cosx，由三角函数知识可得t∈[﹣，]，且sin2x=t2﹣1，可得y=t2+t﹣1，由二次函数区间的最值可得．‎ ‎③由②利用二次函数的性质即可得解；‎ ‎④证明f（﹣x）=f（x），即可判断正误．‎ ‎【解答】解：①∵f（x+2π）=sin[2（x+2π）]+sin（x+2π）+cos（x+2π）=sin2x+sinx+cosx=f（x），‎ ‎∴函数周期为2π，故①正确；‎ ‎②设t=sinx+cosx=sin（x+）∈[﹣，]，‎ ‎∴t2=（sinx+cosx）2=1+sin2x，‎ ‎∴sin2x=t2﹣1，‎ ‎∴y=sin2x+sinx+cosx=t2﹣1+t=t2+t﹣1=（t+）2﹣，t∈[﹣，]，‎ 由二次函数可知，当t∈[﹣，﹣]时，函数y=t2+t﹣1单调递减，当t∈[﹣，]时，函数y=t2+t﹣1单调递增，‎ ‎∴当t=﹣时，函数取最小值ymin=﹣，故②正确；‎ ‎③由②可知y=t2+t﹣1，t∈[﹣，]，故③错误；‎ ‎④∵f（﹣x）=sin[2（﹣x）]+sin（﹣x）+cos（﹣x）=sin（π﹣2x）+sinx+cosx=sin2x+sinx+cosx=f（x），‎ ‎∴函数关于x=对称，故④正确．‎ 故答案为：①②④．‎ ‎　‎ 三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤 ‎17．Sn为数列{an}的前n项和，Sn=2an﹣2（n∈N+）‎ ‎（1）求{an}的通项公式；‎ ‎（2）若bn=nan，求数列{bn}的前n项和Tn．‎ ‎【考点】数列的求和；根的存在性及根的个数判断．‎ ‎【分析】（Ⅰ）通过Sn=2an﹣2与Sn﹣1=2an﹣1﹣2（n≥2）作差，进而可知数列{an}是首项、公比均为2的等比数列，计算即得结论；‎ ‎（Ⅱ）通过（Ⅰ）得bn=3n×2n，进而利用错位相减法计算即得结论．‎ ‎【解答】解：（Ⅰ）依题意，Sn=2an﹣2，Sn﹣1=2an﹣1﹣2（n≥2），‎ 两式相减得：an=2an﹣1，‎ 又∵S1=2a1﹣2，即a1=2，‎ ‎∴数列{an}是首项、公比均为2的等比数列，‎ ‎∴an=2n；‎ ‎（Ⅱ）由（Ⅰ）得bn=3n×2n，‎ ‎∴Tn=3×2+6×22+9×23+…+3n×2n，‎ ‎2Tn=3×22+6×23+…+3（n﹣1）×2n+3n×2n+1，‎ 两式相减得：﹣Tn=3（2+22+23+…+2n）﹣3n×2n+1‎ ‎=3•﹣3n×2n+1‎ ‎=﹣3（n﹣1）2n+1﹣6，‎ ‎∴Tn=6+3（n﹣1）2n+1．‎ ‎　‎ ‎18．△ABC的内角A，B，C的对边a，b，c满足a2+ac=b2．‎ ‎（Ⅰ）求A的取值范围；‎ ‎（Ⅱ）若a=2，A=，求△ABC的面积．‎ ‎【考点】余弦定理；正弦定理．‎ ‎【分析】（1）由余弦定理得a2﹣b2=c2﹣2bccosA，由a2+ac=b2得a2﹣b2=﹣ac，故c2﹣2bccosA=﹣ac，即cosA=，因为a+c＞b，所以cosA，得出A的范围；‎ ‎（2）将A=和a=2分别代入a2+ac=b2和b2+c2﹣a2=2bccosA，联立方程组解出b，c，使用S=bcsinA求出面积．‎ ‎【解答】解：（1）由余弦定理得a2=b2+c2﹣2bccosA，∴a2﹣b2=c2﹣2bccosA，又∵a2+ac=b2，∴a2﹣b2=﹣ac．‎ ‎∴c2﹣2bccosA=﹣ac，∴cosA=，∵a+c＞b，∴cosA．∴0＜A＜．‎ ‎（2）∵a2+ac=b2，∴4+2c=b2，∵b2+c2﹣a2=2bccosA，∴b2+c2﹣4=bc，‎ 联立方程组，解得b=2，c=4．‎ S△ABC=bcsinA==2．‎ ‎　‎ ‎19．已知四棱锥P﹣ABCD，底面ABCD为菱形，△PAB是等边三角形，∠ABC=60°，AB=2，PC=‎ ‎（1）证明：平面PAB⊥平面ABCD；‎ ‎（2）求二面角B﹣PC﹣D的余弦值．‎ ‎【考点】二面角的平面角及求法；平面与平面垂直的判定．‎ ‎【分析】（1）取AB中点O，连结OP，OC，AC，推导出OP⊥AB，OP⊥OC，从而OP⊥面ABC，由此能证明平面PAB⊥平面ABCD．‎ ‎（2）以O为原点，OB，OC，OP为x，y，z轴，建立空间直角坐标系，利用向量法能求出二面角B﹣PC﹣D的余弦值．‎ ‎【解答】证明：（1）取AB中点O，连结OP，OC，AC，‎ ‎∵△PAB是等边三角形，∴OP=，且OP⊥AB，‎ 由题意知△ABC为等边三角形，且OC=，‎ 在△POC中，∵OC2+OP2=CP2，∴OP⊥OC，‎ ‎∴OP⊥面ABC，‎ ‎∵OP⊂平面PAB，∴平面PAB⊥平面ABCD．‎ 解：（2）以O为原点，OB，OC，OP为x，y，z轴，建立空间直角坐标系，‎ 则O（0，0，0），B（1，0，0），C（0，，0），P（0，0，），A（﹣1，0，0），D（﹣2，，0），‎ 设=（x，y，z）是平面PBC的法向量，‎ ‎=（﹣1，，0），=（﹣1，0，），‎ 则，取x=，得=（），‎ 设平面PCD的法向量=（a，b，c），‎ ‎=（0，，﹣），=（﹣2，，﹣），‎ 则，取b=1，得=（0，1，1）＜‎ cos＜＞==，‎ 由图形得二面角B﹣PC﹣D的平面角为钝角，‎ ‎∴二面角B﹣PC﹣D的余弦值为﹣．‎ ‎　‎ ‎20．甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为，，，乙队每人答对的概率都是．设每人回答正确与否相互之间没有影响，用ξ表示甲队总得分．‎ ‎（Ⅰ）求随机变量ξ的分布列及其数学期望E（ξ）；‎ ‎（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．‎ ‎【考点】条件概率与独立事件；离散型随机变量的期望与方差．‎ ‎【分析】（Ⅰ）由题设知ξ的可能取值为0，1，2，3，分别求出P（ξ=0），P（ξ=1），P（ξ=2），P（ξ=3），由此能求出随机变量ξ的分布列和数学期望E（ξ）．‎ ‎（Ⅱ）设“甲队和乙队得分之和为4”为事件A，“甲队比乙队得分高”为事件B，分别求出P（A），P（AB），再由P（B/A）=，能求出结果．‎ ‎【解答】解：（Ⅰ）由题设知ξ的可能取值为0，1，2，3，‎ P（ξ=0）=（1﹣）（1﹣）（1﹣）=，‎ P（ξ=1）=（1﹣）（1﹣）+（1﹣）××（1﹣）+（1﹣）（1﹣）×=，‎ P（ξ=2）=++=，‎ P（ξ=3）==，‎ ‎∴随机变量ξ的分布列为：‎ ‎ ξ ‎ 0‎ ‎1‎ ‎2‎ ‎ 3‎ P 数学期望E（ξ）=0×+1×+2×+3×=．‎ ‎（Ⅱ）设“甲队和乙队得分之和为4”为事件A，“甲队比乙队得分高”为事件B，‎ 则P（A）=++=，‎ P（AB）==，‎ P（B|A）===．‎ ‎　‎ ‎21．已知椭圆C： +=1（a＞b＞0）的焦点和一个顶点在圆x2+y2=4上．‎ ‎（1）求椭圆的方程；‎ ‎（2）已知点P（﹣3，2），若斜率为1的直线l与椭圆G相交于A、B两点，试探讨以AB为底边的等腰三角形ABP是否存在？若存在，求出直线l的方程，若不存在，说明理由．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（Ⅰ）设椭圆G的右焦点为F（c，0），由题意可得：b=c，且b2+c2=8，由此能求出椭圆G的方程．‎ ‎（Ⅱ）以AB为底的等腰三角形ABP存在．设斜率为1的直线l的方程为y=x+m，代入中，得：3x2+4mx+2m2﹣8=0，由此利用根的判别式、韦达定理，结合已知条件能求出直线l的方程．‎ ‎【解答】解：（Ⅰ）设椭圆G的右焦点为F（c，0），‎ 由题意可得：b=c，且b2+c2=8，∴b2=c2=4，‎ 故a2=b2+c2=8，‎ ‎∴椭圆G的方程为 ‎（Ⅱ）以AB为底的等腰三角形ABP存在．理由如下 设斜率为1的直线l的方程为y=x+m，代入中，‎ 化简得：3x2+4mx+2m2﹣8=0，①‎ 因为直线l与椭圆G相交于A，B两点，‎ ‎∴△=16m2﹣12（2m2﹣8）＞0，‎ 解得﹣2，②‎ 设A（x1，y1），B（x2，y2），则，．③‎ 于是AB的中点M（x0，y0）满足=﹣，．‎ 已知点P（﹣3，2），若以AB为底的等腰三角形ABP存在，‎ 则kPM=﹣1，即=﹣1，④，将M（﹣）代入④式，‎ 得m=3∈（﹣2，2）满足②‎ 此时直线l的方程为y=x+3．‎ ‎　‎ ‎22．已知函数f（x）=•e﹣ax（a＞0）．‎ ‎（1）当a=2时，求曲线y=f（x）在x=处的切线方程；‎ ‎（2）讨论方程f（x）﹣1=0根的个数．‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】（1）当a=2时，求函数的导数，利用导数的几何意义进行求解即可．‎ ‎（2）由f（x）﹣1=0得f（x）=1，求函数的导数f′（x），判断函数的单调性，利用函数单调性和最值之间的关系进行判断即可．‎ ‎【解答】解：（Ⅰ）当a=2时，f（x）=•e﹣2x．f（）=3e﹣1，‎ 又f′（x）=•e﹣2x，∴f′（）=2e﹣1，‎ 故所求切线方程为y﹣3e﹣1=2e﹣1（x﹣），即y=x+．‎ ‎（Ⅱ）方程f（x）﹣1=0即f（x）=1．‎ f（x）的定义域为（﹣∞，1）∪（1，+∞），‎ 当x＜﹣1或x＞1时，易知f（x）＜0，故方程f（x）=1无解；‎ 故只需考虑﹣1≤x≤1的情况，‎ f′（x）=•e﹣2x，‎ 当＜a≤2时，f′（x）≥0，所以f（x）区间[﹣1，1）上是增函数，又易知f（0）=1，‎ 所以方程f（x）=1只有一个根0；‎ 当a＞2时，由f′（x）=0可得x=±，且0＜＜1，‎ 由f′（x）＞0可得﹣1≤x＜﹣或＜x＜1，‎ 由f′（x）＜0可得﹣＜x＜，‎ 所以f（x）单调增区间为[﹣1，﹣）和（，1）上是增函数，‎ f（x）单调减区间为（﹣，），‎ 由上可知f（）＜f（0）＜f（﹣），即f（）＜1＜f（﹣），‎ 在区间（﹣，）上f（x）单调递减，且f（0）=1，‎ 所以方程f（x）=1有唯一的根x=0；‎ 在 区间[﹣1，﹣）上f（x）单调递增，且f（﹣1）=0＜1，f（﹣）＞1，‎ 所以方程f（x）=1存在唯一的根0‎ 在区间（，1）上，由f（）＜1，x→1时，f（x）→+∞，‎ 所以方程f（x）=1有唯一的根；‎ 综上所述：当0＜a≤2时，方程f（x）=1有1个根；‎ 当a＞2时，方程f（x）=1有3个根．‎ ‎　‎ ‎2016年8月13日