河南省普通高中高考数学适应性试卷理科解析

河南省普通高中高考数学适应性试卷理科解析

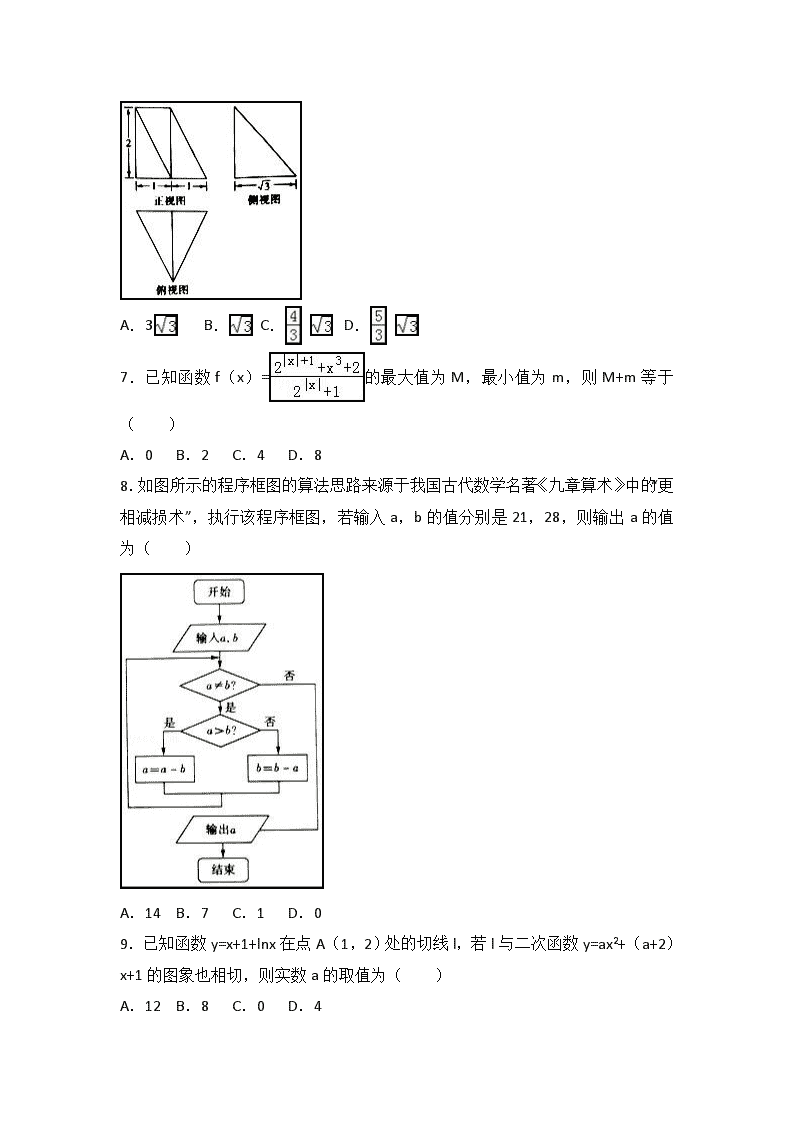
‎2017年河南省普通高中高考数学适应性试卷（理科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合A={x|x2﹣2x﹣3＞0}，B={x|lg（x﹣2）≤1}，则（∁RA）∪B=（　　）‎ A．（﹣1，12） B．（2，3） C．（2，3] D．[﹣1，12]‎ ‎2．欧拉（Leonhard Euler，国籍瑞士）是科学史上最多产的一位杰出的数学家，他发明的公式eix=cosx+isinx（i为虚数单位），将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，这个公式在复变函数理论中占用非常重要的地位，被誉为“数学中的天桥”，根据此公式可知，e﹣4i表示的复数在复平面中位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3．下列命题正确的是（　　）‎ A．∃x0∈R，sinx0+cosx0=‎ B．∀x≥0且x∈R，2x＞x2‎ C．已知a，b为实数，则a＞2，b＞2是ab＞4的充分条件 D．已知a，b为实数，则a+b=0的充要条件是=﹣1‎ ‎4．已知圆O：x2+y2=4（O为坐标原点）经过椭圆C： +=1（a＞b＞0）的短轴端点和两个焦点，则椭圆C的标准方程为（　　）‎ A． +=1 B． +=1‎ C． +=1 D． +=1‎ ‎5．已知等差数列{an}满足a1=1，an+2﹣an=6，则a11等于（　　）‎ A．31 B．32 C．61 D．62‎ ‎6．某几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．3 B． C． D． ‎ ‎7．已知函数f（x）=的最大值为M，最小值为m，则M+m等于（　　）‎ A．0 B．2 C．4 D．8‎ ‎8．如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b的值分别是21，28，则输出a的值为（　　）‎ A．14 B．7 C．1 D．0‎ ‎9．已知函数y=x+1+lnx在点A（1，2）处的切线l，若l与二次函数y=ax2+（a+2）x+1的图象也相切，则实数a的取值为（　　）‎ A．12 B．8 C．0 D．4‎ ‎10．已知△ABC的三个顶点的坐标为A（0，1），B（1，0），C（0，﹣2），O为坐标原点，动点M满足||=1，则|++的最大值是（　　）‎ A． B． C．﹣1 D．﹣1‎ ‎11．已知双曲线C：﹣=1（a＞0，b＞0）的左、右焦点分别为F1，F2，O为坐标原点，点P是双曲线在第一象限内的点，直线PO，PF2分别交双曲线C的左、右支于另一点M，N，若|PF1|=2|PF2|，且∠MF2N=120°，则双曲线的离心率为（　　）‎ A． B． C． D．‎ ‎12．定义在R上的函数f（x），当x∈[0，2]时，f（x）=4（1﹣|x﹣1|），且对于任意实数x∈[2n﹣2，2n+1﹣2]（n∈N*，n≥2），都有f（x）=f（﹣1）．若g（x）=f（x）﹣logax有且只有三个零点，则a的取值范围是（　　）‎ A．[2，10] B．[，] C．（2，10） D．[2，10）‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13．已知实数x，y满足条件若目标函数z=2x+y的最小值为3，则其最大值为　　．‎ ‎14．设二项式展开式中的常数项为a，则的值为　　．‎ ‎15．已知A，B，C是球O的球面上三点，且为该球面上的动点，球心O到平面ABC的距离为球半径的一半，则三棱锥D﹣ABC体积的最大值为　　．‎ ‎16．已知函数fn（x）=a1x+a2x2+a3x3+…+anxn，且fn（﹣1）=（﹣1）nn，n∈N*‎ ‎，设函数g（n）=，若bn=g（2n+4），n∈N*，则数列{bn}的前n（n≥2）项和Sn等于　　．‎ ‎　‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17．已知向量=（2cosx，sinx），=（cosx，2cosx），函数f（x）=•﹣1．‎ ‎（Ⅰ）求函数f（x）的单调递减区间；‎ ‎（Ⅱ）在锐角△ABC中，内角A、B、C的对边分别为a，b，c，tanB=，对任意满足条件的A，求f（A）的取值范围．‎ ‎18．某品牌的汽车4S店，对最近100例分期付款购车情况进行统计，统计结果如表所示，已知分9期付款的频率为0.4；该店经销一辆该品牌的汽车．若顾客分3期付款，其利润为1万元；分6期或9期付款，其利润为2万元；分12期付款，其利润为3万元．‎ ‎ 付款方式 分3期 ‎ 分6期 ‎ 分9期 ‎ 分12期 ‎ ‎ 频数 ‎20 ‎ ‎20 ‎ a ‎ b ‎ ‎（1）若以表中计算出的频率近似替代概率，从该店采用分期付款购车的顾客（数量较大）中随机抽取3位顾客，求事件A：“至多有1位采用分6期付款”的概率P（A）；‎ ‎（2）按分层抽样的方式从这100位顾客中抽出5人，再从抽出的5人中随机抽取3人，记该店在这3人身上赚取的总利润为随机变量η，求η的分布列及数学期望E（η）．‎ ‎19．如图所示，已知长方体ABCD中，为DC的中点．将△‎ ADM沿AM折起，使得AD⊥BM．‎ ‎（1）求证：平面ADM⊥平面ABCM；‎ ‎（2）是否存在满足的点E，使得二面角E﹣AM﹣D为大小为．若存在，求出相应的实数t；若不存在，请说明理由．‎ ‎20．设抛物线的顶点在坐标原点，焦点F在y轴正半轴上，过点F的直线交抛物线于A，B两点，线段AB的长是8，AB的中点到x轴的距离是3．‎ ‎（1）求抛物线的标准方程；‎ ‎（2）设直线m在y轴上的截距为6，且与抛物线交于P，Q两点，连结QF并延长交抛物线的准线于点R，当直线PR恰与抛物线相切时，求直线m的方程．‎ ‎21．已知函数．‎ ‎（1）当a=1时，求函数f（x）的单调区间；‎ ‎（2）若﹣1＜x＜1时，均有f（x）≤0成立，求实数a的取值范围．‎ ‎　‎ 四、请考生在第22、23两题中任选一题作答，注意：只能做所选定的题目，如果多做，则按所做的第一题计分，作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．4-4坐标系与参数方程 ‎22．在平面直角坐标系xoy中，曲线C1的参数方程为（θ为参数），以坐标原点O为极点，x轴的正半轴为极轴，与直角坐标系xoy取相同的单位长度建立极坐标系，曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ．‎ ‎（1）化曲线C1，C2的方程为普通方程，并说明它们分别表示什么曲线；‎ ‎（2）设曲线C2与x轴的一个交点的坐标为P（m，0）（m＞0），经过点P作斜率为1的直线，l交曲线C2于A，B两点，求线段AB的长．‎ ‎　‎ 五、4-5不等式选讲 ‎23．已知f（x）=|2x﹣1|+x+的最小值为m．‎ ‎（1）求m的值；‎ ‎（2）已知a，b，c是正实数，且a+b+c=m，求证：2（a3+b3+c3）≥ab+bc+ca﹣3abc．‎ ‎　‎ ‎2017年河南省普通高中高考数学适应性试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合A={x|x2﹣2x﹣3＞0}，B={x|lg（x﹣2）≤1}，则（∁RA）∪B=（　　）‎ A．（﹣1，12） B．（2，3） C．（2，3] D．[﹣1，12]‎ ‎【考点】交、并、补集的混合运算．‎ ‎【分析】首先化简集合A，B，进而算出∁RA，然后根据并集的定义进行求解．‎ ‎【解答】解：∵集合A={x|x2﹣2x﹣3＞0}={x|x＜﹣1或x＞3}‎ ‎∴∁RA={x|﹣1≤x≤3}=[﹣1，3]‎ ‎∵B={x|lg（x﹣2）≤1}，‎ ‎∴，‎ 解得2＜x≤12，‎ ‎∴B=（2，12]‎ ‎∴（∁RA）∪B=[﹣1，12]‎ 故选：D．‎ ‎　‎ ‎2．欧拉（Leonhard Euler，国籍瑞士）是科学史上最多产的一位杰出的数学家，他发明的公式eix=cosx+isinx（i为虚数单位），将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，这个公式在复变函数理论中占用非常重要的地位，被誉为“数学中的天桥”，根据此公式可知，e﹣4i表示的复数在复平面中位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【考点】复数的代数表示法及其几何意义．‎ ‎【分析】e﹣4i=cos（﹣4）+isin（﹣4），再利用诱导公式与三角函数求值即可得出．‎ ‎【解答】解：e﹣4i=cos（﹣4）+isin（﹣4），∵cos（﹣4）=cos[π+（4﹣π）]=﹣cos（4﹣π）＜0，sin（﹣4）=﹣sin[π+（4﹣π）]=sin（4﹣π）＞0，‎ ‎∴e﹣4i表示的复数在复平面中位于第二象限．‎ 故选：B．‎ ‎　‎ ‎3．下列命题正确的是（　　）‎ A．∃x0∈R，sinx0+cosx0=‎ B．∀x≥0且x∈R，2x＞x2‎ C．已知a，b为实数，则a＞2，b＞2是ab＞4的充分条件 D．已知a，b为实数，则a+b=0的充要条件是=﹣1‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】根据sinx+cosx=sin（x+）≤＜，判断A错误；‎ 举例说明x=2时2x=x2=4，判断B错误；‎ 根据a＞2，b＞2时ab＞4，判断充分性成立C正确；‎ 举例说明a=b=0时=﹣1不成立，判断D错误．‎ ‎【解答】解：对于A，∀x∈R，sinx+cosx=sin（x+）≤＜正确，‎ ‎∴该命题的否定是假命题，A错误；‎ 对于B，当x=2时，2x=x2=4，∴B错误；‎ 对于C，a，b为实数，当a＞2，b＞2时，ab＞4，充分性成立，‎ 是充分条件，C正确；‎ 对于D，a，b为实数，a+b=0时，若a=b=0，则=﹣1不成立，‎ ‎∴不是充要条件，D错误．‎ 故选：C．‎ ‎　‎ ‎4．已知圆O：x2+y2=4（O为坐标原点）经过椭圆C： +=1（a＞b＞0）的短轴端点和两个焦点，则椭圆C的标准方程为（　　）‎ A． +=1 B． +=1‎ C． +=1 D． +=1‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】根据圆O：x2+y2=4（O为坐标原点）经过椭圆C： +=1（a＞b＞0）的短轴端点和两个焦点，可得b，c，a，‎ ‎【解答】解：∵圆O：x2+y2=4（O为坐标原点）经过椭圆C： +=1（a＞b＞0）的短轴端点和两个焦点，‎ ‎∴b=2，c=2，则a2=b2+c2=8．‎ ‎∴椭圆C的标准方程为：，‎ 故选：B ‎　‎ ‎5．已知等差数列{an}满足a1=1，an+2﹣an=6，则a11等于（　　）‎ A．31 B．32 C．61 D．62‎ ‎【考点】等差数列的通项公式．‎ ‎【分析】由等差数列的性质依次求出a3，a5，a7，a9，a11．‎ ‎【解答】解：∵等差数列{an}满足a1=1，an+2﹣an=6，‎ ‎∴a3=6+1=7，‎ a5=6+7=13，‎ a7=6+13=19，‎ a9=6+19=25，‎ a11=6+25=31．‎ 故选：A．‎ ‎　‎ ‎6．某几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．3 B． C． D． ‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】由三视图可得，几何体为底面为正视图，高为的四棱锥，即可求出几何体的体积．‎ ‎【解答】解：由三视图可得，几何体为底面为正视图，高为的四棱锥，体积为=，‎ 故选B．‎ ‎　‎ ‎7．已知函数f（x）=的最大值为M，最小值为m，则M+m等于（　　）‎ A．0 B．2 C．4 D．8‎ ‎【考点】函数的最值及其几何意义．‎ ‎【分析】设g（x）=，得到g（x）为奇函数，得到g（x）max+g（x）min=0，相加可得答案．‎ ‎【解答】解：f（x）==2+，‎ ‎ 设g（x）=，‎ ‎∴g（﹣x）=﹣g（x），‎ ‎∴g（x）为奇函数，‎ ‎∴g（x）max+g（x）min=0‎ ‎∵M=f（x）max=2+g（x）max，m=f（x）min=2+g（x）min，‎ ‎∴M+m=2+g（x）max+2+g（x）min=4，‎ 故选：C ‎　‎ ‎8．如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b的值分别是21，28，则输出a的值为（　　）‎ A．14 B．7 C．1 D．0‎ ‎【考点】程序框图．‎ ‎【分析】由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．‎ ‎【解答】解：由a=21，b=28，不满足a＞b，‎ 则b变为28﹣21=7，‎ 由b＜a，则a变为21﹣7=14，‎ 由b＜a，则a变为14﹣7=7，‎ 由a=b=7，‎ 则输出的a=7．‎ 故选：B．‎ ‎　‎ ‎9．已知函数y=x+1+lnx在点A（1，2）处的切线l，若l与二次函数y=ax2+（a+2）x+1的图象也相切，则实数a的取值为（　　）‎ A．12 B．8 C．0 D．4‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】求出y=x+1+lnx的导数，求得切线的斜率，可得切线方程，再由于切线与曲线y=ax2+（a+2）x+1相切，有且只有一切点，进而可联立切线与曲线方程，根据△=0得到a的值．‎ ‎【解答】解：y=x+1+lnx的导数为y′=1+，‎ 曲线y=x+1+lnx在x=1处的切线斜率为k=2，‎ 则曲线y=x+1+lnx在x=1处的切线方程为y﹣2=2x﹣2，即y=2x．‎ 由于切线与曲线y=ax2+（a+2）x+1相切，‎ y=ax2+（a+2）x+1可联立y=2x，‎ 得ax2+ax+1=0，‎ 又a≠0，两线相切有一切点，‎ 所以有△=a2﹣4a=0，‎ 解得a=4．‎ 故选：D．‎ ‎　‎ ‎10．已知△ABC的三个顶点的坐标为A（0，1），B（1，0），C（0，﹣2），O为坐标原点，动点M满足||=1，则|++的最大值是（　　）‎ A． B． C．﹣1 D．﹣1‎ ‎【考点】平面向量的坐标运算．‎ ‎【分析】设点M的坐标是（x，y），由两点之间的距离公式化简||=1，判断出动点M的轨迹，由向量的坐标运算求出++，表示出|++|并判断几何意义，转化为圆外一点与圆上点的距离最值问题，即可求出答案．‎ ‎【解答】解：设点M的坐标是（x，y），‎ ‎∵C（0，﹣2），且||=1，‎ ‎∴，则x2+（y+2）2=1，‎ 即动点M的轨迹是以C为圆心、1为半径的圆，‎ ‎∵A（0，1），B（1，0），‎ ‎∴++=（x+1，y+1），‎ 则|++|=，几何意义表示：‎ 点M（x，y）与点A（﹣1，﹣1）之间的距离，即圆C上的点与点A（﹣1，﹣1）的距离，‎ ‎∵点A（﹣1，﹣1）在圆C外部，‎ ‎∴|++|的最大值是|AC|+1=+1=，‎ 故选A．‎ ‎　‎ ‎11．已知双曲线C：﹣=1（a＞0，b＞0）的左、右焦点分别为F1，F2，O为坐标原点，点P是双曲线在第一象限内的点，直线PO，PF2分别交双曲线C的左、右支于另一点M，N，若|PF1|=2|PF2|，且∠MF2N=120°，则双曲线的离心率为（　　）‎ A． B． C． D．‎ ‎【考点】直线与椭圆的位置关系．‎ ‎【分析】由题意，|PF1|=2|PF2|，|PF1|﹣|PF2|=2a，可得|PF1|=4a，|PF2|=2a，由∠MF2N=120°，可得∠F1PF2=120°，由余弦定理可得4c2=16a2+4a2﹣2•4a•2a•cos120°，即可求出双曲线C的离心率．‎ ‎【解答】解：由题意，|PF1|=2|PF2|，‎ 由双曲线的定义可得，|PF1|﹣|PF2|=2a，‎ 可得|PF1|=4a，|PF2|=2a，‎ 由四边形PF1MF2为平行四边形，‎ 又∠MF2N=120°，可得∠F1PF2=120°，‎ 在三角形PF1F2中，由余弦定理可得 ‎4c2=16a2+4a2﹣2•4a•2a•cos120°，‎ 即有4c2=20a2+8a2，即c2=7a2，‎ 可得c=a，‎ 即e==．‎ 故选B．‎ ‎　‎ ‎12．定义在R上的函数f（x），当x∈[0，2]时，f（x）=4（1﹣|x﹣1|），且对于任意实数x∈[2n﹣2，2n+1﹣2]（n∈N*，n≥2），都有f（x）=f（﹣1）．若g（x）=f（x）﹣logax有且只有三个零点，则a的取值范围是（　　）‎ A．[2，10] B．[，] C．（2，10） D．[2，10）‎ ‎【考点】根的存在性及根的个数判断；函数零点的判定定理．‎ ‎【分析】由g（x）=f（x）﹣logax=0，得f（x）=logax，分别作出函数f（x）和y=logax的图象，利用数形结合即可得到结论．‎ ‎【解答】解：当x∈[0，2]时，f（x）=4（1﹣|x﹣1|），‎ 当n=2时，x∈[2，6]，此时﹣1∈[0，2]，则f（x）=f（﹣1）=×4（1﹣|﹣1﹣1|）=2（1﹣|﹣2|），‎ 当n=3时，x∈[6，14]，此时﹣1∈[2，6]，则f（x）=f（﹣1）=×2（1﹣|﹣|）=1﹣|﹣|，‎ 由g（x）=f（x）﹣logax=0，得f（x）=logax，分别作出函数f（x）和y=loga x的图象，‎ 若0＜a＜1，则此时两个函数图象只有1个交点，不满足条件．‎ 若a＞1，当对数函数图象经过A时，两个图象只有2个交点，当图象经过点B时，两个函数有4个交点，‎ 则要使两个函数有3个交点，则对数函数图象必须在A点以下，B点以上，‎ ‎∵f（4）=2，f（10）=1，∴A（4，2），B（10，1），‎ 即满足，‎ 即，解得，‎ 即2＜a＜10，‎ 故选：C．‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13．已知实数x，y满足条件若目标函数z=2x+y的最小值为3，则其最大值为　7　．‎ ‎【考点】简单线性规划．‎ ‎【分析】作出不等式组对应的平面区域，利用目标函数z=2x+y的最小值为3，建立条件关系即可求出m的值，然后求解最大值即可．‎ ‎【解答】解：目标函数z=2x+y的最小值为3，‎ ‎∴y=﹣2x+z，要使目标函数z=﹣2x+y的最小值为3，‎ 作出不等式组对应的平面区域如图：‎ 则目标函数经过点A截距最小，‎ 由，解得A（2，﹣1），同时A也在直线﹣2x+y+m=0，‎ 解得m=5，‎ 目标函数z=2x+y经过B时取得最大值 由，解得B（3，1），‎ z的最大值为：7．‎ 故答案为：7．‎ ‎　‎ ‎14．设二项式展开式中的常数项为a，则的值为　﹣　．‎ ‎【考点】二项式系数的性质．‎ ‎【分析】利用二项式定理的通项公式可得a，再利用微积分基本定理即可得出．‎ ‎【解答】解：二项式展开式中的通项公式：Tr+1==（﹣1）r．‎ 令6﹣=0，解得r=4．‎ ‎∴常数项a==15，‎ 则=cos3xdx==﹣．‎ 故答案为：﹣．‎ ‎　‎ ‎15．已知A，B，C是球O的球面上三点，且为该球面上的动点，球心O到平面ABC的距离为球半径的一半，则三棱锥D﹣ABC体积的最大值为　　．‎ ‎【考点】棱柱、棱锥、棱台的体积．‎ ‎【分析】由题意画出图形，求出三角形ABC外接圆的半径，设出球的半径，利用直角三角形中的勾股定理求得球的半径，则三棱锥D﹣ABC体积的最大值可求．‎ ‎【解答】解：如图，在△ABC中，∵，‎ ‎∴由余弦定理可得cosA=，则A=120°，‎ ‎∴sinA=．‎ 设△ABC外接圆的半径为r，则，得r=3．‎ 设球的半径为R，则，解得．‎ ‎∵，‎ ‎∴三棱锥D﹣ABC体积的最大值为．‎ 故答案为：．‎ ‎　‎ ‎16．已知函数fn（x）=a1x+a2x2+a3x3+…+anxn，且fn（﹣1）=（﹣1）nn，n∈N*，设函数g（n）=，若bn=g（2n+4），n∈N*，则数列{bn}的前n（n≥2）项和Sn等于　2n+n﹣1　．‎ ‎【考点】数列的求和．‎ ‎【分析】由分段函数，求得bn=a，再由函数fn（x），求得n=1时，a1=1，将n换为n﹣1，作差可得an=2n﹣1，进而得到 bn=2n﹣1+1，再由数列的求和方法：分组求和，结合等比数列的求和公式，计算即可得到所求和．‎ ‎【解答】解：由函数g（n）=，‎ 可得bn=g（2n+4）=g（2n﹣1+2）=g（2n﹣2+1）=a，‎ 由函数fn（x）=a1x+a2x2+a3x3+…+anxn，且fn（﹣1）=（﹣1）nn，‎ 可得﹣a1+a2﹣a3+…+an（﹣1）n=（﹣1）nn，①‎ n=1时，﹣a1=﹣1，可得a1=1；‎ n≥2时，﹣a1+a2﹣a3+…+an﹣1（﹣1）n﹣1=（﹣1）n﹣1（n﹣1），②‎ ‎①﹣②可得an（﹣1）n=（﹣1）nn﹣（﹣1）n﹣1（n﹣1），‎ 化简可得an=2n﹣1，对n=1也成立．‎ 则bn=a=2n﹣1+1，‎ 则数列{bn}的前n（n≥2）项和Sn等于（1+2+4+…+2n﹣1）+n ‎=+n=2n+n﹣1．‎ 故答案为：2n+n﹣1．‎ ‎　‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17．已知向量=（2cosx，sinx），=（cosx，2cosx），函数f（x）=•﹣1．‎ ‎（Ⅰ）求函数f（x）的单调递减区间；‎ ‎（Ⅱ）在锐角△ABC中，内角A、B、C的对边分别为a，b，c，tanB=，对任意满足条件的A，求f（A）的取值范围．‎ ‎【考点】余弦定理；平面向量数量积的运算．‎ ‎【分析】（Ⅰ）根据函数f（x）=•﹣1．利用向量的数量积的运算求解f（x），结合三角函数的性质求解单调性即可．‎ ‎（Ⅱ）tanB=求解．‎ ‎【解答】解：（Ⅰ）向量=（2cosx，sinx），=（cosx，2cosx），‎ 函数f（x）=•﹣1．‎ 则f（x）=2cos2x+2sinxcosx﹣1=sin2x+cos2x=2sin（2x）‎ 由，‎ 解得：≤x≤，（k∈Z）．‎ 故得函数f（x）的单调递减区间为[，]，（k∈Z）‎ ‎（Ⅱ）由tanB=，即：，‎ ‎∵cosB=‎ ‎∴sinB=．‎ 又∵△ABC是锐角，‎ ‎∴B=．‎ 则＜A＜‎ 由（Ⅰ）可知f（A）=2sin（2A）‎ 那么：2A∈（，）‎ 则sin（2A）∈（，1）‎ 故得f（A）的取值范围是（﹣1，2）‎ ‎　‎ ‎18．某品牌的汽车4S店，对最近100例分期付款购车情况进行统计，统计结果如表所示，已知分9期付款的频率为0.4；该店经销一辆该品牌的汽车．若顾客分3期付款，其利润为1万元；分6期或9期付款，其利润为2万元；分12期付款，其利润为3万元．‎ ‎ 付款方式 分3期 ‎ 分6期 ‎ 分9期 ‎ 分12期 ‎ ‎ 频数 ‎20 ‎ ‎20 ‎ a ‎ b ‎ ‎（1）若以表中计算出的频率近似替代概率，从该店采用分期付款购车的顾客（数量较大）中随机抽取3位顾客，求事件A：“至多有1位采用分6期付款”的概率P（A）；‎ ‎（2）按分层抽样的方式从这100位顾客中抽出5人，再从抽出的5人中随机抽取3人，记该店在这3人身上赚取的总利润为随机变量η，求η的分布列及数学期望E（η）．‎ ‎【考点】离散型随机变量的期望与方差；列举法计算基本事件数及事件发生的概率．‎ ‎【分析】（1）由=0.4，得a=40，20+a+20+b=100，解得b．记分期付款的期数为ξ，依题意即可得出其概率．进而定点“购买该品牌汽车的3为顾客中至多有1位采用3期付款”的概率P（A）．‎ ‎（2）按分层抽样的方式从这100位顾客中抽出5人，则顾客分3期付款与分6期付款的各为1人，分9期付款的为2人，分12期付款为1人．则η的可能取值为5，6，7．利用相互独立与互斥事件的概率计算公式可得其概率，进而得到分布列与数学期望．‎ ‎【解答】解：（1）由=0.4，得a=40，‎ ‎∵20+a+20+b=100，∴b=20‎ 记分期付款的期数为ξ，依题意得：‎ P（ξ=3）==0.2，P（ξ=6）==0.2，P（ξ=9）==0.4，P（ξ=12）=‎ ‎=0.2．‎ 则“购买该品牌汽车的3为顾客中至多有1位采用3期付款”的概率 P（A）=+=0.896．‎ ‎（2）按分层抽样的方式从这100位顾客中抽出5人，则顾客分3期付款与分6期付款的各为1人，分9期付款的为2人，分12期付款为1人．则η的可能取值为5，6，7．‎ P（η=5）=P（ξ=3）×P（ξ=6）×P（ξ=9）+P（ξ=3）×P（ξ=9）×P（ξ=9）=+=．‎ P（η=6）=P（ξ=3）×P（ξ=6）×P（ξ=12）+P（ξ=6）×P（ξ=9）×P（ξ=9）+P（ξ=3）×P（ξ=9）×P（ξ=12）==，‎ P（η=7）=P（ξ=6）×P（ξ=9）×P（ξ=12）+P（ξ=9）×P（ξ=9）×P（ξ=12）==．‎ 列表如下：‎ η ‎5‎ ‎6‎ ‎7‎ P ‎0.3‎ ‎0.4‎ ‎0.3‎ 所以η的数学期望E（η）=5×0.3+6×0.4+7×0.3=6（万元）．‎ ‎　‎ ‎19．如图所示，已知长方体ABCD中，为DC的中点．将△ADM沿AM折起，使得AD⊥BM．‎ ‎（1）求证：平面ADM⊥平面ABCM；‎ ‎（2）是否存在满足的点E，使得二面角E﹣AM﹣D为大小为．若存在，求出相应的实数t；若不存在，请说明理由．‎ ‎【考点】与二面角有关的立体几何综合题；平面与平面垂直的判定．‎ ‎【分析】（1）推导出BM⊥AM，AD⊥BM，从而BM⊥平面ADM，由此能证明平面ADM⊥平面ABCM．‎ ‎（2）以M为原点，MA为x轴，MB为y轴，过M作平面ABCM的垂线为z轴，建立空间直角坐标系，利用向量法能求出存在满足的点E，使得二面角E﹣AM﹣D为大小为，并能求出相应的实数t的值．‎ ‎【解答】证明：（1）∵长方形ABCD中，AB=2AD=2，M为DC的中点，‎ ‎∴AM=BM=2，AM2+BM2=AB2，∴BM⊥AM，‎ ‎∵AD⊥BM，AD∩AM=A，∴BM⊥平面ADM，‎ 又BM⊂平面ABCM，∴平面ADM⊥平面ABCM．‎ 解：（2）以M为原点，MA为x轴，MB为y轴，过M作平面ABCM的垂线为z轴，‎ 建立空间直角坐标系，‎ 则A（2，0，0），B（0，2，0），D（1，0，1），M（0，0，0），‎ ‎=（0，2，0），=（1，﹣2，1），==（t，2﹣2t，1），‎ 设平面AME的一个法向量为=（x，y，z），‎ 则，‎ 取y=t，得=（0，t，2t﹣2），‎ 由（1）知平面AMD的一个法向量=（0，1，0），‎ ‎∵二面角E﹣AM﹣D为大小为，‎ ‎∴cos===，‎ 解得t=或t=2（舍），‎ ‎∴存在满足的点E，使得二面角E﹣AM﹣D为大小为，相应的实数t的值为．‎ ‎　‎ ‎20．设抛物线的顶点在坐标原点，焦点F在y轴正半轴上，过点F的直线交抛物线于A，B两点，线段AB的长是8，AB的中点到x轴的距离是3．‎ ‎（1）求抛物线的标准方程；‎ ‎（2）设直线m在y轴上的截距为6，且与抛物线交于P，Q两点，连结QF并延长交抛物线的准线于点R，当直线PR恰与抛物线相切时，求直线m的方程．‎ ‎【考点】直线与抛物线的位置关系．‎ ‎【分析】（1）设抛物线的方程为x2=2py（p＞0），求出准线方程，运用抛物线的定义和中位线定理，可得2（3+）=8，解得p，即可得到抛物线的方程；‎ ‎（2）设直线PQ的方程为y=kx+6，代入抛物线的方程，运用韦达定理，结合导数求得切线的斜率，再由两点的方斜率公式，以及三点共线的条件：斜率相等，化简整理解方程可得k的值，客人得到直线m的方程．‎ ‎【解答】解：（1）设抛物线的方程为x2=2py（p＞0），‎ 准线方程为y=﹣，‎ 由抛物线的定义可得|AF|+|BF|=|AB|=2（3+）=8，‎ 解得p=2，‎ 即有抛物线的方程为x2=4y；‎ ‎（2）设直线PQ的方程为y=kx+6，代入抛物线的方程，可得 x2﹣4kx﹣24=0，‎ 设P（x1，），Q（x2，），‎ 可得x1+x2=4k，x1x2=﹣24，‎ 由y=x2的导数为y′=x，‎ 设R（t，﹣1），可得kPR==x1，‎ 可得t=x1﹣，‎ 再由Q，F，R共线，可得=，‎ 消去t，可得=，‎ 即有16x1x2=4（x12+x22）﹣16﹣（x1x2）2，‎ 即有16×（﹣24）=4[（4k）2+2×24]﹣16﹣242，‎ 解方程可得k=±，‎ 即有直线m的方程为y=±x+6．‎ ‎　‎ ‎21．已知函数．‎ ‎（1）当a=1时，求函数f（x）的单调区间；‎ ‎（2）若﹣1＜x＜1时，均有f（x）≤0成立，求实数a的取值范围．‎ ‎【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．‎ ‎【分析】（Ⅰ）当a=1时，f（x）的定义域为（﹣1，1）∪（1，+∞），‎ 求出f′（x）=，即可求单调区间；‎ ‎（Ⅱ）f′（x）=，‎ 分（1）a≤0，（2）当a＞0，讨论单调性及最值即可．‎ ‎【解答】解：（Ⅰ）当a=1时，f（x）的定义域为（﹣1，1）∪（1，+∞），‎ f′（x）=，‎ 当﹣1＜x＜0或＞3时，f′（x）＞0，当0＜x＜1或1＜x＜3，f′（x）＜0，‎ 所以函数f（x）的增区间为（﹣1，0），（3，+∞），减区间为（0，1），（1，3）‎ ‎（Ⅱ）f′（x）=，‎ 当a≤0时，f′（x）＞0恒成立，故0＜x＜1时，f（x）＞f（0）=0，不符合题意．‎ 当a＞0时，由f′（x）=0，得x1=，x2=．‎ 若0＜a＜1，此时0＜x1＜1，对0＜x＜x1，有f′（x）＞0，f（x）＞f（0）=0，不符合题意．‎ 若a＞1，此时﹣1＜x1＜0，对x1＜x＜0，有f′（x）＜0，f（x）＞f（0）=0，不符合题意．‎ 若a=1，由（Ⅰ）知，函数f（x）在x=0处取得最大值0，符合题意，‎ 综上实数a的取值为1．‎ ‎　‎ 四、请考生在第22、23两题中任选一题作答，注意：只能做所选定的题目，如果多做，则按所做的第一题计分，作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．4-4坐标系与参数方程 ‎22．在平面直角坐标系xoy中，曲线C1的参数方程为（θ为参数），以坐标原点O为极点，x轴的正半轴为极轴，与直角坐标系xoy取相同的单位长度建立极坐标系，曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ．‎ ‎（1）化曲线C1，C2的方程为普通方程，并说明它们分别表示什么曲线；‎ ‎（2）设曲线C2与x轴的一个交点的坐标为P（m，0）（m＞0），经过点P作斜率为1的直线，l交曲线C2于A，B两点，求线段AB的长．‎ ‎【考点】参数方程化成普通方程．‎ ‎【分析】（1）根据sin2θ+cos2θ=1消去曲线C1‎ 的参数θ可得普通方程；根据ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得曲线C2的普通方程；‎ ‎（2）令曲线C2的y=0，求解P的坐标，可得过P的直线方程，参数方程的几何意义求解即可．‎ ‎【解答】解：（1）曲线C1的参数方程为，消去参数可得：，表示焦点在y轴上的椭圆方程．‎ 曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ，可得ρ2=2ρcosθ﹣4ρsinθ，‎ ‎∴x2+y2=2x﹣4y，整理得（x﹣1）2+（y+2）2=5，表示以（1，﹣2）为圆心，半径r=5的圆．‎ ‎（2）曲线C2与x轴的一个交点的坐标为P（m，0）（m＞0），令y=0，解得x=2，‎ ‎∴P（2，0），可得直线l：y=x﹣2．‎ 将曲线C1的参数方程带入直线l可得： sinθ=2cosθ﹣2．‎ 整理可得：cos（）=，即θ=2kπ或，（k∈Z）．‎ 那么：A（2，0），B（﹣1，﹣3），‎ ‎∴|AB|=．‎ ‎　‎ 五、4-5不等式选讲 ‎23．已知f（x）=|2x﹣1|+x+的最小值为m．‎ ‎（1）求m的值；‎ ‎（2）已知a，b，c是正实数，且a+b+c=m，求证：2（a3+b3+c3）≥ab+bc+ca﹣3abc．‎ ‎【考点】不等式的证明．‎ ‎【分析】（1）讨论当x≥时，当x＜时，去掉绝对值，运用一次函数的单调性，可得最小值；‎ ‎（2）由a+b+c=1，先证a3+b3≥a2b+b2a，由作差法可得，即有a3+b3≥ab﹣abc，同理可得b3+c3≥bc﹣abc，c3+a3≥ca﹣abc，累加即可得证．‎ ‎【解答】解：（1）当x≥时，f（x）=3x﹣递增，且f（x）≥﹣=1；‎ 当x＜时，f（x）=﹣x递减，且f（x）＞﹣=1；‎ 综上可得x=时，f（x）取得最小值1，即m=1；‎ ‎（2）证明：a，b，c是正实数，且a+b+c=1，‎ 由a3+b3﹣a2b﹣b2a=a2（a﹣b）+b2（b﹣a）=（a﹣b）（a2﹣b2）=（a+b）（a﹣b）2≥0，‎ 即有a3+b3﹣a2b﹣b2a≥0，即a3+b3≥a2b+b2a=ab（a+b）=ab（1﹣c）=ab﹣abc，‎ 可得a3+b3≥ab﹣abc，‎ 同理可得b3+c3≥bc﹣abc，‎ c3+a3≥ca﹣abc，‎ 上面三式相加可得，2（a3+b3+c3）≥ab+bc+ca﹣3abc，‎ 当且仅当a=b=c=取得等号．‎ ‎　‎ ‎2017年3月23日