宁波市中考数学试卷及答案word版

宁波市中考数学试卷及答案word版

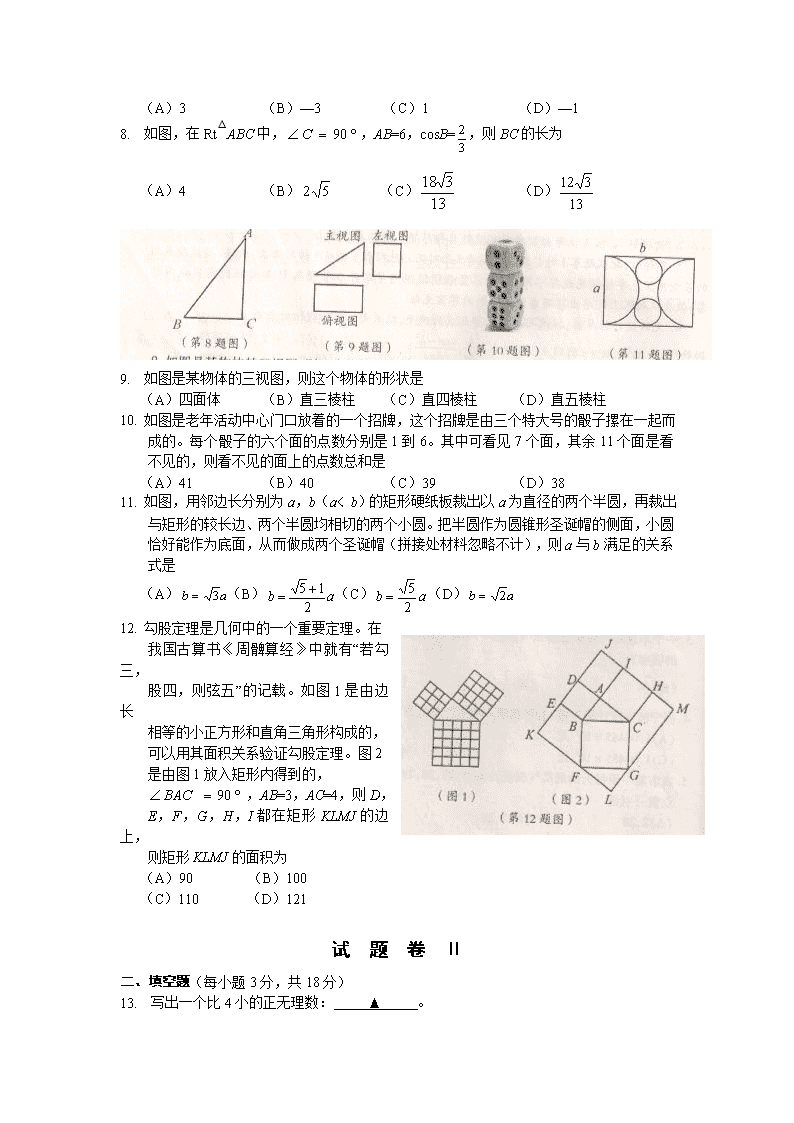
宁波市2012年初中毕业生学业考试 数 学 试 题 姓名 准考证号 ‎ 考生须知：‎ 1． 全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷，试题卷共6页，有三个大题，26个小题。满分120分，考试时间为120分钟。‎ 2． 请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上。‎ 3． 答题时，把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满。将试题卷Ⅱ的答案用黑色字迹钢笔或签字笔书写，答案必须按照题号顺序在答题卷Ⅱ各题目规定区域作答，坐在试题卷上或超出答题卷区域书写的答案无效。‎ 4． 允许使用计算器，但没有近似计算要求的试题，结果都不能用近似数表示。‎ 抛物线y=ax2+bx+c的顶点坐标为 试 题 卷 Ⅰ 一、选择题（每小题3分，共36分，在每小题给出的四个选项中，只有一个符合题目要求）‎ ‎1. （—2）0的值为 ‎ （A）—2 （B）0 （C）1 （D）2‎ ‎2. 下列交通标志图案是轴对称图形的是 3. 一个不透明口袋中装着只有颜色不同的1个红球和2个白球，搅匀后从中摸出一个球，摸到白球的概率为 ‎（A） （B） （C） （D）1‎ ‎4. 据宁波市统计局年报，去年我市人均生产总值为104485元，104485元用科学计数法表示为 ‎（A）1.04485×106元 （B）0.104485×106元 ‎（C）1.04485×105元 （D）10.4485×104元 ‎5. 我市某一周每天最高气温统计如下：27，28，29，29，30，29，28（单位：℃）。则这组数据的极差与众数分别是 ‎ （A）2,28 （B）3,29 （C）2,27 （D）3,28‎ ‎6. 下列计算正确的是 ‎ （A）（B） （C） （D）‎ ‎7. 已知实数x，y满足，则x—y等于 ‎ （A）3 （B）—3 （C）1 （D）—1‎ ‎8. 如图，在Rt△ABC中，，AB=6，cosB=，则BC的长为 ‎ （A）4 （B） （C） （D）‎ ‎9. 如图是某物体的三视图，则这个物体的形状是 ‎ （A）四面体 （B）直三棱柱 （C）直四棱柱 （D）直五棱柱 ‎10. 如图是老年活动中心门口放着的一个招牌，这个招牌是由三个特大号的骰子摞在一起而成的。每个骰子的六个面的点数分别是1到6。其中可看见7个面，其余11个面是看不见的，则看不见的面上的点数总和是 ‎ （A）41 （B）40 （C）39 （D）38‎ ‎11. 如图，用邻边长分别为a，b（a﹤b）的矩形硬纸板裁出以a为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆。把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽（拼接处材料忽略不计），则a与b满足的关系式是 ‎ （A）（B）（C）（D）‎ ‎12. 勾股定理是几何中的一个重要定理。在 ‎ 我国古算书《周髀算经》中就有“若勾三， ‎ 股四，则弦五”的记载。如图1是由边长 相等的小正方形和直角三角形构成的，‎ 可以用其面积关系验证勾股定理。图2‎ 是由图1放入矩形内得到的，‎ ‎，AB=3，AC=4，则D，‎ E，F，G，H，I都在矩形KLMJ的边上，‎ 则矩形KLMJ的面积为 ‎ （A）90 （B）100‎ ‎（C）110 （D）121‎ 试 题 卷 Ⅱ 二、填空题（每小题3分，共18分）‎ ‎13. 写出一个比4小的正无理数： ▲ 。‎ ‎14. 分式方程的解是 ▲ 。‎ ‎15. 如图是七年级（1）班学生参加课外兴趣小组人数的扇形统计图。如果参加外语兴趣小组的人数是12人，那么参加绘画兴趣小组的人数是 ▲ 人。‎ ‎16. 如图，AE∥BD，C是BD上的点，且AB=BC，，则 ‎ ▲ 度。‎ ‎17. 把二次函数的图象绕原点旋转180°后得到的图象解析式为 ‎ ▲ 。‎ ‎18. 如图，△ABC中，，，AB=，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为 ▲ 。‎ 三、解答题（本大题共8小题，共66分）‎ ‎19. （本题共6分）计算：‎ ‎20. （本题6分）用同样大小的黑色棋子按如图所示的规律摆放：‎ ‎（1）第5个图形有多少颗黑色棋子？‎ ‎（2）第几个图形有2013颗黑色棋子？请说明理由。‎ ‎21. （本题6分）如图，已知一次函数与反比例函数的图象交于点 ‎ A（—4，—2）和B（a，4）。‎ ‎（1）求反比例函数的解析式和点B的坐标；‎ ‎（2）根据图象回答，当x在什么范围内时，一次函数的值 ‎ 大于反比例函数的值？‎ ‎22. （本题8分）某学校要成立一支由6名女生组成的礼仪队，初三两个班各选6名女生，分别组成甲队和乙队参加选拔。每位女生的身高统计如下图，部分统计量如下表：‎ ‎（1）求甲队身高的中位数；‎ ‎（2）求乙队身高的平均数及身高不小于1.70米的频率；‎ ‎（3）如果选拔的标准是身高越整齐越好，那么甲、乙两队中哪一队将被录取？请说明 理由。‎ 23. ‎（本题8分）如图，在△ABC中，BE是它的角平分线，，D在AB边上以DB为直径的半圆O经过点E，交BC于点F。‎ ‎（1）求证：AC是⊙O 的切线；‎ ‎（2）已知sinA=，⊙O的半径为4，求图中阴影部分的 ‎ 面积。‎ ‎24. （本题10分）为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费。下表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息：‎ 自来水销售价格 污水处理价格 每户每月用水量 单价：元∕吨 单价：元∕吨 ‎17吨及以下 a ‎0.80‎ 超过17吨但不超过30吨的部分 b ‎0.80‎ 超过30吨的部分 ‎6.00‎ ‎0.80‎ ‎（说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费）‎ 已知小王家2012年4月份用水20吨，交水费66元；5月份用水25吨，交水费91元。‎ ‎（1）求a，b的值；‎ ‎（2）随着夏天的到来，用水量将增加。为了节省开支，小王计划把6月份的水费控制 在不超过家庭收入的2%。若小王的月收入为9200元，则小王家6月份最多能 用水多少吨？‎ ‎25. （本题10分）邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形。如图1，□ABCD中，若AB=1，BC=2，则□ABCD为1阶准菱形。‎ ‎（1）判断与推理：‎ ‎①邻边长分别为2和3的平行四边形是 ▲ 阶准菱形；‎ ‎②小明为了剪去一个菱形，进行如下操作：如图2，把□ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE。请证明四边形ABEF是菱形。‎ ‎（2）操作、探究与计算：‎ ‎①已知□ABCD是邻边长分别为1，a（a＞1），且是3阶准菱形，请画出□ABCD及裁剪线的示意图，并在图形下方写出a的值；‎ ‎②已知□ABCD的邻边长分别为a，b（a＞b），满足a=6b+r，b=5r，请写出□ABCD是几阶准菱形。‎ ‎ ‎ ‎26. （本题12分）如图，二次函数y=ax2+bx+c的图象交x轴于A（—1,0），B（2,0），交y轴于C（0，—2），过A，C画直线。‎ ‎（1）求二次函数的解析式；‎ ‎（2）点P在x轴正半轴上，且PA=PC，求OP的长；‎ ‎（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H。‎ ‎①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；‎ ‎②若⊙M的半径为，求点M的坐标。‎