中考数学试卷分类汇编解析动态问题

中考数学试卷分类汇编解析动态问题

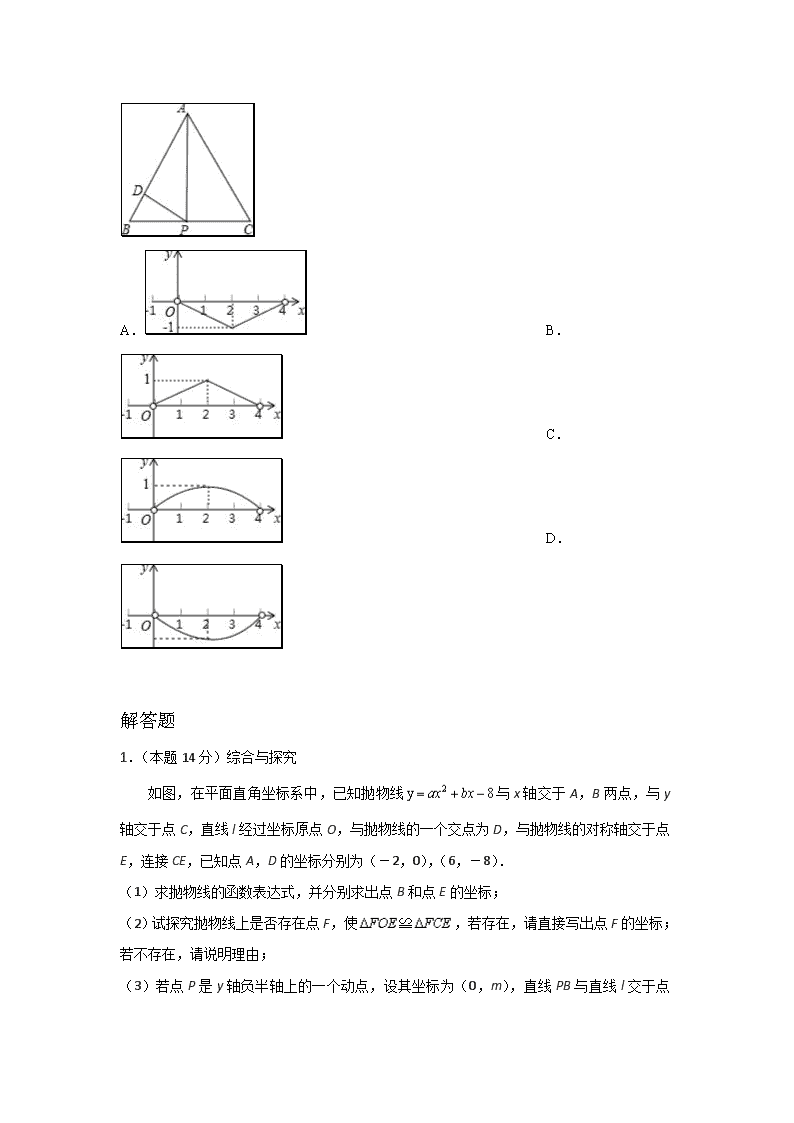
动态问题 一、选择题 ‎1. （2016·湖北鄂州） 如图，O是边长为4cm的正方形ABCD的中心，M是BC的中点，动点P由A开始沿折线A—B—M方向匀速运动，到M时停止运动，速度为1cm/s. 设P点的运动时间为t(s)，点P的运动路径与OA、OP所围成的图形面积为S(cm2)，则描述面积S(cm2)与时间t(s)的关系的图像可以是（ A ）‎ ‎2. 如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（　C　）‎ A．6 B．2+1 C．9 D．‎ ‎3. 如图，在△ABC中，∠ACB=90°，AC=4，BC=2．P是AB边上一动点，PD⊥AC于点D，点E在P的右侧，且PE=1，连结CE．P从点A出发，沿AB方向运动，当E到达点B时，P停止运动．在整个运动过程中，图中阴影部分面积S1+S2的大小变化情况是（　C　）‎ A．一直减小 B．一直不变 C．先减小后增大 D．先增大后减小 ‎4．如图，正△ABC的边长为4，点P为BC边上的任意一点（不与点B、C重合），且∠APD=60°，PD交AB于点D．设BP=x，BD=y，则y关于x的函数图象大致是（　C　） ‎ ‎ ‎ A． B． C． D．‎ ‎ ‎ 解答题 ‎1．（本题14分）综合与探究 如图，在平面直角坐标系中，已知抛物线与x轴交于A，B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（－2，0），（6，－8）．‎ ‎（1）求抛物线的函数表达式，并分别求出点B和点E的坐标；‎ ‎（2）试探究抛物线上是否存在点F，使≌，若存在，请直接写出点F的坐标；若不存在，请说明理由；‎ ‎（3）若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线l交于点 Q．试探究：当m为何值时，是等腰三角形．‎ 解答：（1）抛物线经过点A（－2，0），D（6，－8），‎ 解得…………………………………（1分）‎ 抛物线的函数表达式为……………………………（2分）‎ ‎，抛物线的对称轴为直线．又抛物线与x轴交于A，B两点，点A的坐标为（－2，0）．点B的坐标为（8，0）…………………（4分）‎ 设直线l的函数表达式为．点D（6，－8）在直线l上，6k=－8，解得．‎ 直线l的函数表达式为………………………………………………………（5分）‎ 点E为直线l和抛物线对称轴的交点．点E的横坐标为3，纵坐标为，即点E的坐标为（3，－4）……………………………………………………………………（6分）‎ ‎（2）抛物线上存在点F，使≌．‎ 点F的坐标为（）或（）．……………………………………（8分）‎ ‎（3）解法一：分两种情况： ‎ ‎①当时，是等腰三角形．‎ 点E的坐标为（3，－4），，过点E作直线ME//PB，交y轴于点M，交x轴于点H，则，……………………………………（9分）‎ 点M的坐标为（0，－5）．‎ 设直线ME的表达式为，，解得，ME的函数表达式为，令y=0，得，解得x=15，点H的坐标为（15，0）…（10分）‎ 又MH//PB，，即，……………………………（11分）‎ ‎②当时，是等腰三角形．‎ 当x=0时，，点C的坐标为（0，－8），‎ ‎，OE=CE，，又因为，，‎ ‎，CE//PB………………………………………………………………（12分）‎ 设直线CE交x轴于点N，其函数表达式为，，解得，CE的函数表达式为，令y=0，得，，点N的坐标为 ‎（6，0）………………………………………………………………（13分）‎ CN//PB，，，解得………………（14分）‎ 综上所述，当m的值为或时，是等腰三角形．‎ 解法二：‎ 当x=0时， ，点C的坐标为（0，－8），点E的坐标为 ‎（3，－4），，，OE=CE，，设抛物线的对称轴交直线PB于点M，交x轴于点H．分两种情况：‎ ① 当时，是等腰三角形．‎ ‎，，CE//PB………………………………………（9分）‎ 又HM//y轴，四边形PMEC是平行四边形，，‎ ‎，HM//y轴，‎ ‎∽，……………………………………………………（10分）‎ ‎………………………………………………………（11分）‎ ‎②当时，是等腰三角形．‎ 轴，∽，，……………（12分）‎ ‎，，轴，∽，…………………………………………………（13分）‎ ‎………………（14分）‎ 当m的值为或时，是等腰三角形．‎ ‎2．如图所示，梯形ABCD中，AB∥DC，∠B=90°，AD=15，AB=16，BC=12，点E是边AB上的动点，点F是射线CD上一点，射线ED和射线AF交于点G，且∠AGE=∠DAB．‎ ‎（1）求线段CD的长；‎ ‎（2）如果△AEC是以EG为腰的等腰三角形，求线段AE的长；‎ ‎（3）如果点F在边CD上（不与点C、D重合），设AE=x，DF=y，求y关于x的函数解析式，并写出x的取值范围．‎ 解：（1）作DH⊥AB于H，如图1，‎ 易得四边形BCDH为矩形，‎ ‎∴DH=BC=12，CD=BH，‎ 在Rt△ADH中，AH===9，‎ ‎∴BH=AB﹣AH=16﹣9=7，‎ ‎∴CD=7；‎ ‎（2）当EA=EG时，则∠AGE=∠GAE，‎ ‎∵∠AGE=∠DAB，‎ ‎∴∠GAE=∠DAB，‎ ‎∴G点与D点重合，即ED=EA，‎ 作EM⊥AD于M，如图1，则AM=AD=，‎ ‎∵∠MAE=∠HAD，‎ ‎∴Rt△AME∽Rt△AHD，‎ ‎∴AE：AD=AM：AH，即AE：15=：9，解得AE=；‎ 当GA=GE时，则∠AGE=∠AEG，‎ ‎∵∠AGE=∠DAB，‎ 而∠AGE=∠ADG+∠DAG，∠DAB=∠GAE+∠DAG，‎ ‎∴∠GAE=∠ADG，‎ ‎∴∠AEG=∠ADG，‎ ‎∴AE=AD=15，‎ 综上所述，△AEC是以EG为腰的等腰三角形时，线段AE的长为或15；‎ ‎（3）作DH⊥AB于H，如图2，则AH=9，HE=AE﹣AH=x﹣9，‎ 在Rt△ADE中，DE==，‎ ‎∵∠AGE=∠DAB，∠AEG=∠DEA，‎ ‎∴△EAG∽△EDA，‎ ‎∴EG：AE=AE：ED，即EG：x=x：，‎ ‎∴EG=，‎ ‎∴DG=DE﹣EG=﹣，‎ ‎∵DF∥AE，‎ ‎∴△DGF∽△EGA，‎ ‎∴DF：AE=DG：EG，即y：x=（﹣）：，‎ ‎∴y=（9＜x＜）．‎ ‎3．如图，在平面直角坐标系中，抛物线y=mx2+4mx﹣5m（m＜0）与x轴交于点A、B（点A在点B的左侧），该抛物线的对称轴与直线y=x相交于点E，与x轴相交于点D，点P在直线y=x上（不与原点重合），连接PD，过点P作PF⊥PD交y轴于点F，连接DF．‎ ‎（1）如图①所示，若抛物线顶点的纵坐标为6，求抛物线的解析式；‎ ‎（2）求A、B两点的坐标；‎ ‎（3）如图②所示，小红在探究点P的位置发现：当点P与点E重合时，∠PDF的大小为定值，进而猜想：对于直线y=x上任意一点P（不与原点重合），∠PDF的大小为定值．请你判断该猜想是否正确，并说明理由．‎ 解：（1）∵y=mx2+4mx﹣5m，‎ ‎∴y=m（x2+4x﹣5）=m（x+5）（x﹣1）．‎ 令y=0得：m（x+5）（x﹣1）=0，‎ ‎∵m≠0，‎ ‎∴x=﹣5或x=1．‎ ‎∴A（﹣5，0）、B（1，0）．‎ ‎∴抛物线的对称轴为x=﹣2．‎ ‎∵抛物线的顶点坐标为为6，‎ ‎∴﹣9m=6．‎ ‎∴m=﹣．‎ ‎∴抛物线的解析式为y=﹣x2﹣x+．‎ ‎（2）由（1）可知：A（﹣5，0）、B（1，0）．‎ ‎（3）如图所示：‎ ‎∵OP的解析式为y=x，‎ ‎∴∠AOP=30°．‎ ‎∴∠PBF=60°‎ ‎∵PD⊥PF，FO⊥OD，‎ ‎∴∠DPF=∠FOD=90°．‎ ‎∴∠DPF+∠FOD=180°．‎ ‎∴点O、D、P、F共圆．‎ ‎∴∠PDF=∠PBF．‎ ‎∴∠PDF=60°．‎ ‎4．如图1，在平面直角坐标系xOy中，抛物线y=ax2+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．‎ ‎（1）求抛物线的解析式，并写出其顶点B的坐标；‎ ‎（2）①当P点运动到A点处时，计算：PO=　5　，PH=　5　，由此发现，PO　=　PH（填“＞”、“＜”或“=”）；‎ ‎②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想；‎ ‎（3）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．‎ ‎（1）解：∵抛物线y=ax2+1经过点A（4，﹣3），‎ ‎∴﹣3=16a+1，‎ ‎∴a=﹣，‎ ‎∴抛物线解析式为y=﹣x2+1，顶点B（0，1）．‎ ‎（2）①当P点运动到A点处时，∵PO=5，PH=5，‎ ‎∴PO=PH，‎ 故答案分别为5，5，=．‎ ‎②结论：PO=PH．‎ 理由：设点P坐标（m，﹣ m2+1），‎ ‎∵PH=2﹣（﹣m2+1）=m2+1‎ PO==m2+1，‎ ‎∴PO=PH．‎ ‎（3）∵BC==，AC==，AB==4‎ ‎∴BC=AC，‎ ‎∵PO=PH，‎ 又∵以P，O，H为顶点的三角形与△ABC相似，‎ ‎∴PH与BC，PO与AC是对应边，‎ ‎∴=，设点P（m，﹣ m2+1），‎ ‎∴=，‎ 解得m=±1，‎ ‎∴点P坐标（1，）或（﹣1，）．‎ ‎5．已知：如图，在矩形ABCD中，Ab=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：‎ ‎（1）当t为何值时，△AOP是等腰三角形？‎ ‎（2）设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；‎ ‎（3）在运动过程中，是否存在某一时刻t，使S五边形S五边形OECQF：S△ACD=9：16？若存在，求出t的值；若不存在，请说明理由；‎ ‎（4）在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．‎ 解：（1）∵在矩形ABCD中，Ab=6cm，BC=8cm，‎ ‎∴AC=10，‎ ‎①当AP=PO=t，如图1，‎ 过P作PM⊥AO，‎ ‎∴AM=AO=，‎ ‎∵∠PMA=∠ADC=90°，∠PAM=∠CAD，‎ ‎∴△APM∽△ADC，‎ ‎∴，‎ ‎∴AP=t=，‎ ‎②当AP=AO=t=5，‎ ‎∴当t为或5时，△AOP是等腰三角形；‎ ‎（2）作EH⊥AC于H，QM⊥AC于M，DN⊥AC于N，交QF于G，‎ 在△APO与△CEO中，‎ ‎，‎ ‎∴△AOP≌△COE，‎ ‎∴CE=AP=t，‎ ‎∵△CEH∽△ABC，‎ ‎∴，‎ ‎∴EH=，‎ ‎∵DN==，‎ ‎∵QM∥DN，‎ ‎∴△CQM∽△CDN，‎ ‎∴，即，‎ ‎∴QM=，‎ ‎∴DG=﹣=，‎ ‎∵FQ∥AC，‎ ‎∴△DFQ∽△DOC，‎ ‎∴，‎ ‎∴FQ=，‎ ‎∴S五边形OECQF=S△OEC+S四边形OCQF=×5×+（+5）•=﹣t2+t+12，‎ ‎∴S与t的函数关系式为S=﹣t2+t+12；‎ ‎（3）存在，‎ ‎∵S△ACD=×6×8=24，‎ ‎∴S五边形OECQF：S△ACD=（﹣t2+t+12）：24=9：16，‎ 解得t=，t=0，（不合题意，舍去），‎ ‎∴t=时，S五边形S五边形OECQF：S△ACD=9：16；‎ ‎（4）如图3，过D作DM⊥AC于M，DN⊥AC于N，‎ ‎∵∠POD=∠COD，‎ ‎∴DM=DN=，‎ ‎∴ON=OM==，‎ ‎∵OP•DM=3PD，‎ ‎∴OP=5﹣t，‎ ‎∴PM=﹣t，‎ ‎∵PD2=PM2+DM2，‎ ‎∴（8﹣t）2=（﹣t）2+（）2，‎ 解得：t≈15（不合题意，舍去），t≈2.88，‎ ‎∴当t=2.88时，OD平分∠COP．‎ ‎　‎ ‎6．如图1，二次函数y=ax2+bx的图象过点A（﹣1，3），顶点B的横坐标为1．‎ ‎（1）求这个二次函数的表达式；‎ ‎（2）点P在该二次函数的图象上，点Q在x轴上，若以A、B、P、Q为顶点的四边形是平行四边形，求点P的坐标；‎ ‎（3）如图3，一次函数y=kx（k＞0）的图象与该二次函数的图象交于O、C两点，点T为该二次函数图象上位于直线OC下方的动点，过点T作直线TM⊥OC，垂足为点M，且M在线段OC上（不与O、C重合），过点T作直线TN∥y轴交OC于点N．若在点T运动的过程中，为常数，试确定k的值．‎ 解：（1）∵二次函数y=ax2+bx的图象过点A（﹣1，3），顶点B的横坐标为1，‎ 则有解得 ‎∴二次函数y=x2﹣2x，‎ ‎（2）由（1）得，B（1，﹣1），‎ ‎∵A（﹣1，3），‎ ‎∴直线AB解析式为y=﹣2x+1，AB=2，‎ 设点Q（m，0），P（n，n2﹣2n）‎ ‎∵以A、B、P、Q为顶点的四边形是平行四边形，‎ ‎①当AB为对角线时，根据中点坐标公式得，则有，解得或 ‎∴P（1+，2）和（1﹣，2）‎ ‎②当AB为边时，根据中点坐标公式得解得或 ‎∴P（1+，4）或（1﹣，4）．‎ ‎（3）设T（m，m2﹣2m），∵TM⊥OC，‎ ‎∴可以设直线TM为y=﹣x+b，则m2﹣2m=﹣m+b，b=m2﹣2m+，‎ 由解得，‎ ‎∴OM==，ON=m•，‎ ‎∴=，‎ ‎∴k=时， =．‎ ‎∴当k=时，点T运动的过程中，为常数．‎ ‎ ‎