中考数学试卷分类汇编32圆的有关性质

中考数学试卷分类汇编32圆的有关性质

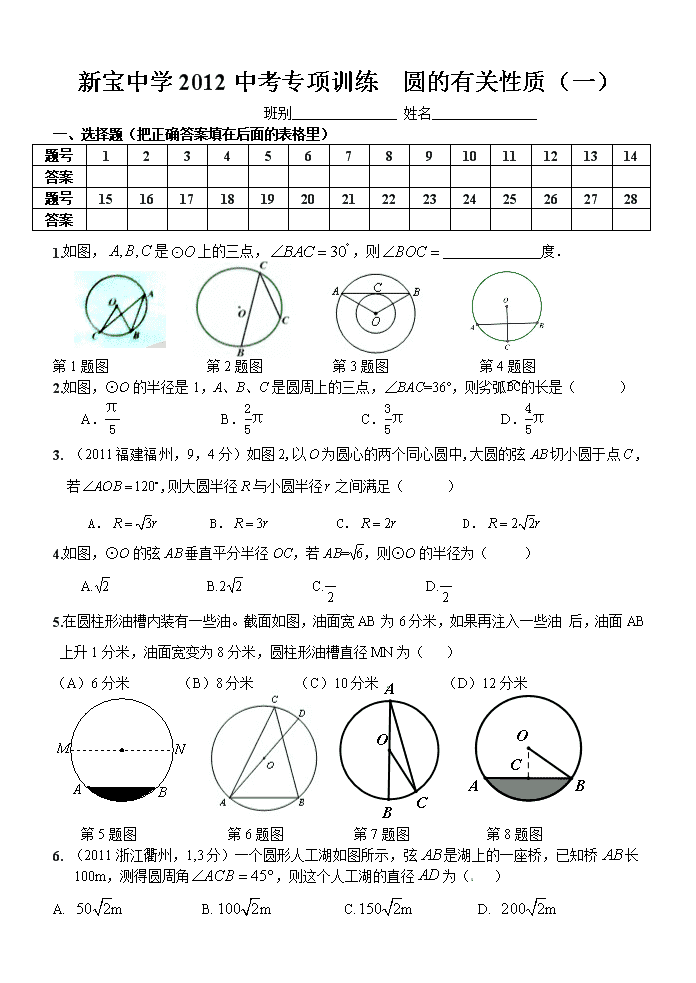
新宝中学2012中考专项训练　圆的有关性质（一）‎ 班别 姓名 ‎ 一、选择题（把正确答案填在后面的表格里）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ 答案 题号 ‎15‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 答案 ‎1.如图，是上的三点，，则 度．‎ 第1题图 第2题图 第3题图 第4题图 ‎ ‎2.如图，⊙O的半径是1，A、B、C是圆周上的三点，∠BAC=36°，则劣弧的长是（ ）‎ A． B．π C．π D．π ‎3. （2011福建福州，9，4分）如图2,以为圆心的两个同心圆中,大圆的弦切小圆于点,若,则大圆半径与小圆半径之间满足（ ）‎ ‎ A． B． C． D． ‎ ‎4.如图，⊙O的弦AB垂直平分半径OC，若AB=，则⊙O的半径为（ ）‎ A. B‎.2 C. D. ‎5.在圆柱形油槽内装有一些油。截面如图，油面宽AB为6分米，如果再注入一些油 后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为（ ）‎ ‎（A）6分米 （B）8分米 （C）10分米 （D）12分米 第5题图 第6题图 第7题图 第8题图 ‎6. （2011浙江衢州，1,3分）一个圆形人工湖如图所示，弦是湖上的一座桥，已知桥长‎100m，测得圆周角，则这个人工湖的直径为（ ）‎ A. B. C. D. ‎ ‎7.如图，的直径，点在上，若,则的度数是（ ）‎ ‎ A. B. C. D. ‎ ‎8. （2011浙江绍兴，6，4分）一条排水管的截面如图所示.已知排水管的截面圆半径，截面圆圆心到水面的距离是6，则水面宽是（ ）‎ ‎ A.16 B‎.10 C.8 D.6‎ ‎9. （2011浙江省，5，3分）如图，小华同学设计了一个圆直径的测量器，标有刻度的尺子OA、OB在O点钉在一起，并使它们保持垂直，在测直径时，把O点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为（ ）‎ A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位 第9题图 第10题图 第11题图 第12题图 ‎ ‎10．（2011四川重庆，6，4分）如图，⊙O是△ABC的外接圆，∠OCB＝40°则∠A的度数等于( )‎ A． 60° B． 50° C． 40° D． 30°‎ ‎11.如图，半径为10的⊙O中，弦AB的长为16，则这条弦的弦心距为（　　）‎ ‎（A）6 （B）8 （C）10 （D）12‎ ‎12. （2011台湾台北，16）如图(六)，为圆O的直径，直线ED为圆O的切线，A、C两点 在圆上，平分∠BAD且交于F点。若∠ADE＝，则∠AFB的度数( )‎ A．97 B．‎104 C．116 D．142‎ ‎13.如图(六)，△ABC的外接圆上，AB、BC、CA三弧的度数比为12：13：11．自BC上取一点D，过D分别作直线AC、直线AB的并行线，且交于E、F两点，则∠EDF的度数为（ ）‎ ‎ A． 55 B． ‎60 C． 65 D． 70‎ A B C O 第13题图 第14题图 第15题图 第16题图 ‎14. （2011甘肃兰州，12，4分）如图，⊙O过点B、C，圆心O在等腰Rt△ABC的内部，∠BAC=90°，OA=1，BC=6。则⊙O的半径为（ ）‎ A．6 B．‎13 ‎ C． D．‎ ‎15. （2011四川成都，7,3分）如图，若AB是⊙0的直径，CD是⊙O的弦，∠ABD=58°， 则∠BCD=（ ）‎ ‎(A)116° (B)32° (C)58° （D)64°‎ ‎16. （2011四川内江，9，3分）如图，⊙O是△ABC的外接圆，∠BAC=60°,若⊙O的半径OC为2，则弦BC的长为 A．1 B． C．2 D．2‎ ‎17. （2011浙江省舟山，6，3分）如图，半径为10的⊙O中，弦AB的长为16，则这条弦的弦心距为（　 　）‎ ‎（A）6 （B）8 （C）10 （D）12‎ 第17题图 第18题图 第19题图 第20题图 ‎ ‎18. （2011江苏南通，8，3分）如图，⊙O的弦AB＝8，M是AB的中点，且OM＝3，则⊙O的半径等于 A. ‎8 B. ‎2 ‎ C. 10 D. 5‎ ‎19. （2011山东临沂，6，3分）如图，⊙O的直径CD＝‎5cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OD＝3：5，则AB 的长是（ ）‎ A．‎2cm B．3cmC．‎4cm D．‎2‎cm ‎20．（2011上海，6，4分）矩形ABCD中，AB＝8，，点P在边AB上，且BP＝3AP，如果圆P是以点P为圆心，PD为半径的圆，那么下列判断正确的是（ ）．‎ ‎(A) 点B、C均在圆P外； (B) 点B在圆P外、点C在圆P内；‎ ‎(C) 点B在圆P内、点C在圆P外； (D) 点B、C均在圆P内．‎ ‎21.如图，AB为⊙O的直径，点C在⊙O上,∠A=30°,则∠B的度数为 （ ） ‎ ‎ A．15° B. 30° C. 45° D. 60°‎ A B C D E 第21题图 第22题图 第23题图 第24题图 ‎ ‎22. （2011四川凉山州，9，4分）如图，，点C在上，且点C不与A、B重合，则的度数为（ ）‎ A．　　 B．或 　　C．　　 D． 或 ‎23. （2011广东肇庆，7，3分）如图，四边形ABCD是圆内接四边形，E是BC 延长线上一点，若∠BAD ＝105°，则∠DCE的大小是 A． 115° B． 105° C． 100° D． 95°‎ ‎24.如图， AB为⊙ O 的直径， CD 为弦， AB ⊥ CD ，如果∠BOC = 70 ，那么∠A的度数为（ ）‎ ‎ A . B . C . D . ‎ 第24题图 第25题图 第26题图 第27题图 ‎25、 （2011浙江省舟山，15，4分）如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧BC于点D，连结CD、OD，给出以下四个结论：①AC∥OD；②；③△ODE∽△ADO；④．其中正确结论的序号是　 　．‎ A. ①④ B ①②④ C ①③④ D ①②③④‎ ‎26. （2011安徽，13，5分）如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O的半径是 ．‎ A B ‎2 C 3 D 6‎ ‎27.（2011江苏扬州，15,3分）如图，⊙O的弦CD与直径AB相交，若∠BAD=50°，则∠ACD= ‎ A 40° B 50° C60° D 70°‎ ‎28如图2，已知⊙O是△ABC的外接圆，‎ 且∠C =70°，则∠OAB =__________.‎ A 40° B 30° ‎ C 50° D 20°‎ 新宝中学2012中考专项训练　圆的有关性质（二）‎ 班别 姓名 ‎ 一、填空题：‎ ‎1. （2011山东日照，14，4分）如图，在以AB为直径的半圆中，有一个边长为1的内接正方形CDEF ‎，则以AC和BC的长为两根的一元二次方程是 ．‎ 第1题图 第2题图 第3题图 第 4 题图 ‎2. （2011山东泰安，23 ，3分）如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧CBA上一点，若∠ABC==320，则∠P的度数为 。‎ ‎3. （2011山东威海，15，3分）如图，⊙O的直径AB与弦CD相交于点E，若AE=5,BE=1,,则∠AED= . ‎ ‎4. （2011浙江杭州，14，4）如图，点A，B，C，D都在⊙O上，的度数等于84°，CA是∠OCD的平分线，则∠ABD十∠CAO= °．‎ ‎5. （2011福建泉州，16，4分）已知三角形的三边长分别为3，4，5，则它的边与半径为1的圆的公共点个数所有可能的情况是 .（写出符合的一种情况即可）‎ ‎6. （2011江苏连云港，15，3分）如图，点D为边AC上一点，点O为边AB上一点，AD=DO.以O为圆心，OD长为半径作半圆，交AC于另一点E，交AB于点F，G，连接EF.若∠BAC=22º，则∠EFG=_____.‎ ‎ 第7题图 ‎7. （2011四川广安，19，3分）如图3所示，若⊙O的半径为‎13cm，点是弦上一动点，且到圆心的最短距离为‎5 cm，则弦的长为________cm ‎8. （ 2011重庆江津， 16，4分）已知如图,在圆内接四边形ABCD中,∠B=30º,则∠D=____________.‎ A B C D 第8题图 ‎9. (2011重庆綦江，13，4分) 如图,已知AB为⊙O的直径，∠CAB＝30°,则∠D＝ .‎ ‎10、如图，在△ABC中，点P是△ABC的内心，则∠PBC+∠PCA+∠PAB= 度.‎ ‎11、(2011江苏南京，13，2分)如图，海边有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°，为了避免触礁，轮船P与A、B的张角∠APB的最大值为______°．‎ A B O P 第9题图 第10题图 第11题图 第12题图 ‎13、（2011江苏无锡，18，2分）如图，以原点O为圆心的圆交x轴于点A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB = 20°，则∠OCD = _____________．‎ y x O A B D C ‎（第13题）‎ ‎14. （2011内蒙古乌兰察布，14，4分）如图，是半径为 6 的⊙D的圆周，C点是上的任意一点， △ABD是等边三角形,则四边形ABCD的周长P的取值范围是 ‎ 第14题图 第15题图 ‎15. （2011湖北荆州，12，4分）如图，⊙O是△ABC的外接圆，CD是直径，∠B＝40°，则∠ACD的度数是　　　.‎ 二、解答题 ‎1. （2011浙江金华，21，8分）如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OA∥PE.‎ ‎（1）求证：AP＝AO；‎ ‎（2）若弦AB＝12，求tan∠OPB的值；‎ ‎（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，‎ 则能构成菱形的四个点为 ，能构成等腰梯形的四个点为 ‎ 或 或 .‎ ‎2.（2011浙江金华，24，12分）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上的一动点，连结OB、AB，并延长AB至点D，使DB＝AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF.‎ ‎（1）当∠AOB＝30°时，求弧AB的长；‎ ‎（2）当DE＝8时，求线段EF的长；‎ ‎（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似，若存在，请求出此时点E的坐标；若不存在，请说明理由.‎ ‎3. （2011山东德州22,10分）●观察计算 当，时， 与的大小关系是_________________．‎ 当，时， 与的大小关系是_________________．‎ ‎●探究证明 如图所示，为圆O的内接三角形，为直径，过C作于D，设，BD=b．‎ ‎（1）分别用表示线段OC，CD；‎ ‎（2）探求OC与CD表达式之间存在的关系 ‎（用含a，b的式子表示）．‎A B C O D ‎●归纳结论 根据上面的观察计算、探究证明，你能得出与的大小关系是：_________________________．‎ ‎●实践应用 要制作面积为‎1平方米的长方形镜框，直接利用探究得出的结论，求出镜框周长的最小值．‎ 新宝中学2012中考专项训练　圆的有关性质（三）‎ 班别 姓名 ‎ ‎1. （2011山东济宁，19，6分）如图，为外接圆的直径，，垂足为点，的平分线交于点，连接，.‎ ‎(1) 求证：； ‎ ‎ (2) 请判断，，三点是否在以为圆心，‎ 以为半径的圆上？并说明理由.‎ ‎2 已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.‎ ‎（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2‎ A B C D E F P ‎.‎ O G ‎（图1）‎ ‎.‎ A B C D E ‎.‎ O G ‎（图2）‎ ‎（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.‎ ‎3. （2011宁波市，25，10分）阅读下面的情境对话，然后解答问题 ‎（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？‎ ‎（2）在RtABC 中， ∠ACB＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若RtABC是奇异三角形，求a：b：c；‎ ‎（3）如图，AB是⊙O的直径，C是上一点（不与点A、B重合），D是半圆的中点，CD在直径AB的两侧，若在⊙O内存在点E使得AE＝AD，CB＝CE．‎ 求证：ACE是奇异三角形；‎ 当ACE是直角三角形时，求∠AOC的度数．‎ ‎4. （2011广东广州市，25，14分）‎ ‎ 如图7，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中 ∠DCE是直角，点D在线段AC上．‎ ‎　（1）证明：B、C、E三点共线；‎ ‎ （2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；‎ ‎ （3）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图8），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明；若不是，说明理由．‎ A B C D E M N O 图7‎ A B C D1‎ E1‎ M1‎ O N1‎ 图8‎ ‎5．（2011江西，21，8分）如图，已知⊙O的半径为2，弦BC的长为，点A为弦BC所对优弧上任意一点（B，C两点除外）。‎ ‎⑴求∠BAC的度数；‎ ‎⑵求△ABC面积的最大值.‎ ‎6. （已知 △ABC，分别以AC和BC为直径作半圆、P是AB的中点.‎ ‎（1）如8，若△ABC是等腰三角形，且AC=BC，在上分别取点E、F，使 则有结论① ②四边形是菱形.请给出结论②的证明；‎ ‎（2）如图9，若（1）中△ABC是任意三角形，其它条件不变，则（1）中的两个结论还成立吗？若成立，请给出证明；‎ ‎（3）如图10，若PC是的切线，求证：‎ B D ‎7. （2011江苏苏州，26,8分）如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD.‎ ‎（1）弦长AB=________（结果保留根号）；‎ ‎（2）当∠D=20°时，求∠BOD的度数；‎ ‎（3）当AC的长度为多少时，以点A、C、D为顶点的三角形与 以B、C、O为顶点的三角形相似？请写出解答过程.‎ 新宝中学2012中考专项训练　圆的有关性质（四）‎ 班别 姓名 ‎ ‎1. （2011江苏苏州，27,8分）已知四边形ABCD是边长为4的正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD.‎ ‎（1）如图①，当PA的长度等于______时，∠PAB=60°；‎ ‎ 当PA的长度等于______时，△PAD是等腰三角形；‎ ‎（2）如图②，以AB边所在的直线为x轴，AD边所在的直线为y轴，建立如图所示的直角坐标系（点A即为原点O），把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.设P点坐标为（a，b），试求2S1S3-S22的最大值，并求出此时a、b的值.‎ ‎2. （2011江苏泰州，26，10分）如图，以点O为圆心的两个同心圆中，矩形ABCD的边BC为大圆的弦，边AD与小圆相切于点M，OM的延长线与BC相交于点N．‎ ‎（1）点N是线段BC的中点吗？为什么？‎ ‎（2）若圆环的宽度（两圆半径之差）为‎6cm，AB=‎5cm，BC=‎10cm，‎ 求小圆的半径．‎ ‎3. （2011湖北黄冈，22，8分）在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．‎ ‎⑴求证△ABD为等腰三角形．‎ ‎⑵求证AC•AF=DF•FE ‎4. 如图，在 Rt△ABC中,∠ACB＝90°，D是AB 边上的一点，以BD为直径的 ⊙0与边 AC 相切于点E，连结DE并延长，与BC的延长线交于点 F . ‎ ‎( 1 ）求证： BD = BF ;‎ ‎( 2 ）若 BC = 12 , AD = 8 ，求 BF 的长．‎ ‎5. （2010湖北孝感，23，10分）如图，等边△ABC内接于⊙O，P是上任一点（点P不与点A、B重合）.连AP、BP，过点C作CM∥BP交PA的延长线于点M.‎ ‎（1）填空：∠APC＝ 度，∠BPC＝ 度；（2分）‎ ‎（2）求证：△ACM∽△BCP；（4分）‎ ‎（3）若PA=1，PB=2，求梯形PBCM的面积. （4分）‎ ‎6. （2011湖北宜昌，21，8分）如图D是△ABC 的边BC 的中点，过AD 延长线上的点E作AD的垂线EF，E为垂足，EF与AB 的延长线相交于点F，点0 在AD 上，AO = CO，BC//EF.‎ ‎(1)证明:AB=AC； ‎ ‎(2)证明:点0 是AABC 的外接圆的圆心；‎ ‎(3)当AB=5,BC=6时，连接BE若∠ABE=90°，求AE的长.‎ ‎ ‎ ‎7.已知：如图，在△ABC中，BC=AC， BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点 E．‎ ‎⑴求证：点D是AB的中点；‎ ‎⑵判断DE与⊙O的位置关系，并证明你的结论；‎ ‎⑶若⊙O的直径为18，cosB =，求DE的长．‎ ‎8. （2011江苏盐城，25，10分）如图，在△ABC中，∠C= 90°，以AB上一点O为圆心，OA长为半径的圆与BC相切于点D，分别交AC、AB于点E、F．‎ ‎（1）若AC=6，AB= 10，求⊙O的半径；‎ ‎（2）连接OE、ED、DF、EF．若四边形BDEF是平行四边形，‎ 试判断四边形OFDE的形状，并说明理由．‎