泉州市2015年中考数学卷

泉州市2015年中考数学卷

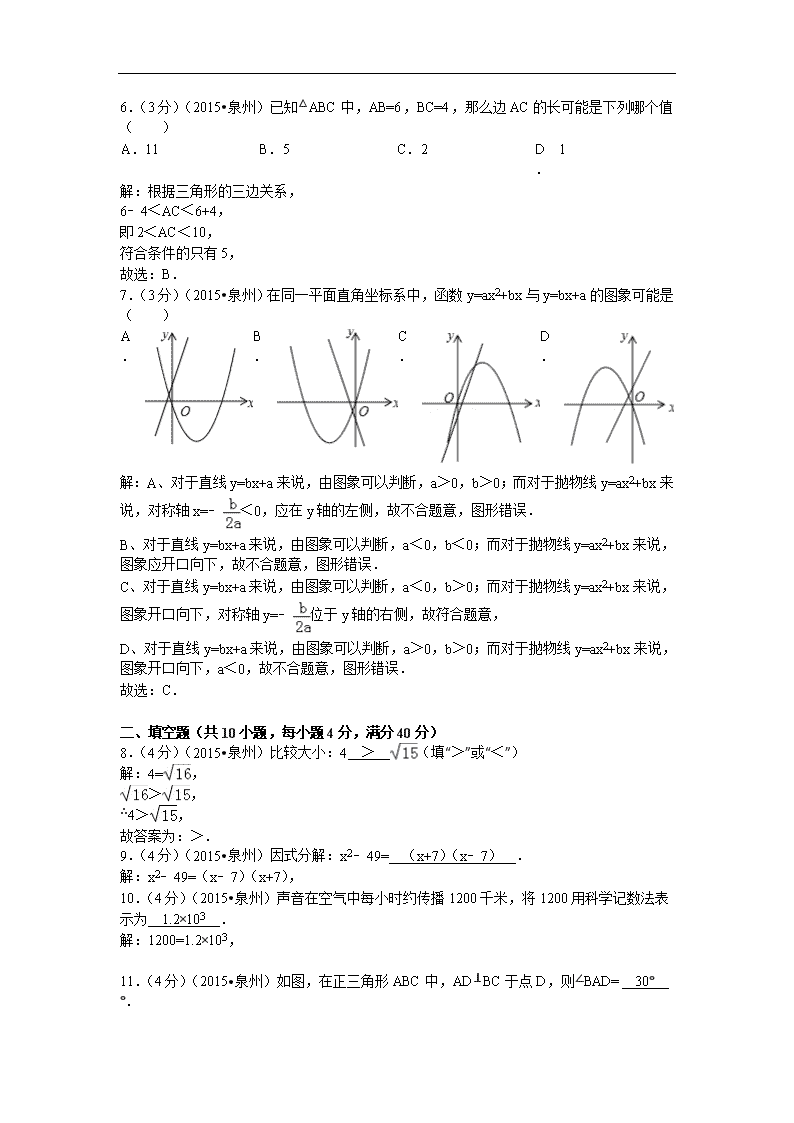
‎2015年福建省泉州市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（共7小题，每小题3分，满分21分）‎ ‎1．（3分）（2015•泉州）﹣7的倒数是（　　）‎ A． 7 B． ﹣7　 C． D． ﹣‎ 解：﹣7的倒数是﹣，故选：D．‎ 点评： 本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．‎ ‎2．（3分）（2015•泉州）计算：（ab2）3=（　　）‎ ‎　 A． 3ab2 B． ab6 C． a3b6 D． a3b2‎ 解：（ab2）3=a3（b2）3=a3b6故选C ‎　‎ ‎3．（3分）（2015•泉州）把不等式x+2≤0的解集在数轴上表示出来，则正确的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 解：解不等式x+2≤0，得x≤﹣2．‎ 表示在数轴上为：．‎ 故选：D．‎ ‎4．（3分）（2015•泉州）甲、乙、丙、丁四人参加训练，近期的10次百米测试平均成绩都是13.2秒，方差如表 ‎ 选手 ‎ 甲 ‎ 乙 ‎ 丙 ‎ 丁 ‎ 方差（秒2）‎ ‎ 0.020‎ ‎ 0.019‎ ‎ 0.021‎ ‎ 0.022‎ 则这四人中发挥最稳定的是（　　）‎ ‎　‎ A．‎ 甲 B．‎ 乙 C．‎ 丙 D．‎ 丁 解：∵0.019＜0.020＜0.021＜0.022，∴乙的方差最小，‎ ‎∴这四人中乙发挥最稳定，故选：B．‎ ‎5．（3分）（2015•泉州）如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5．EC=3，那么平移的距离为（　　）‎ ‎　‎ A．‎ ‎2‎ B．‎ ‎3‎ C．‎ ‎5‎ D．‎ ‎7‎ 解：根据平移的性质，‎ 易得平移的距离=BE=5﹣3=2，‎ 故选A．‎ ‎6．（3分）（2015•泉州）已知△ABC中，AB=6，BC=4，那么边AC的长可能是下列哪个值（　　）‎ ‎　‎ A．‎ ‎11‎ B．‎ ‎5‎ C．‎ ‎2‎ D．‎ ‎1‎ 解：根据三角形的三边关系，‎ ‎6﹣4＜AC＜6+4，‎ 即2＜AC＜10，‎ 符合条件的只有5，‎ 故选：B．‎ ‎7．（3分）（2015•泉州）在同一平面直角坐标系中，函数y=ax2+bx与y=bx+a的图象可能是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 解：A、对于直线y=bx+a来说，由图象可以判断，a＞0，b＞0；而对于抛物线y=ax2+bx来说，对称轴x=﹣＜0，应在y轴的左侧，故不合题意，图形错误．‎ B、对于直线y=bx+a来说，由图象可以判断，a＜0，b＜0；而对于抛物线y=ax2+bx来说，图象应开口向下，故不合题意，图形错误．‎ C、对于直线y=bx+a来说，由图象可以判断，a＜0，b＞0；而对于抛物线y=ax2+bx来说，图象开口向下，对称轴y=﹣位于y轴的右侧，故符合题意，‎ D、对于直线y=bx+a来说，由图象可以判断，a＞0，b＞0；而对于抛物线y=ax2+bx来说，图象开口向下，a＜0，故不合题意，图形错误．‎ 故选：C．‎ ‎　‎ 二、填空题（共10小题，每小题4分，满分40分）‎ ‎8．（4分）（2015•泉州）比较大小：4　＞　（填“＞”或“＜”）‎ 解：4=，‎ ‎＞，‎ ‎∴4＞，‎ 故答案为：＞．‎ ‎9．（4分）（2015•泉州）因式分解：x2﹣49=　（x+7）（x﹣7）　．‎ 解：x2﹣49=（x﹣7）（x+7），‎ ‎10．（4分）（2015•泉州）声音在空气中每小时约传播1200千米，将1200用科学记数法表示为　1.2×103　．‎ 解：1200=1.2×103，‎ ‎　‎ ‎11．（4分）（2015•泉州）如图，在正三角形ABC中，AD⊥BC于点D，则∠BAD=　30°　°．‎ 解：∵△ABC是等边三角形，‎ ‎∴∠BAC=60°，‎ ‎∵AB=AC，AD⊥BC，‎ ‎∴∠BAD=∠BAC=30°，‎ 故答案为：30°．‎ ‎　‎ ‎12．（4分）（2015•泉州）方程x2=2的解是　±　．‎ 解：x2=2，‎ x=±．‎ 故答案为±．‎ ‎13．（4分）（2015•泉州）计算：+=　2　．‎ 解：原式===2，‎ 故答案为：2‎ ‎　‎ ‎14．（4分）（2015•泉州）如图，AB和⊙O切于点B，AB=5，OB=3，则tanA=　　．‎ 解：∵直线AB与⊙O相切于点B，‎ 则∠OBA=90°．‎ ‎∵AB=5，OB=3，‎ ‎∴tanA==．‎ 故答案为：‎ ‎15．（4分）（2015•泉州）方程组的解是　　．‎ 解：，‎ ‎①+②得：3x=3，即x=1，‎ 把x=1代入①得：y=﹣3，‎ 则方程组的解为，‎ 故答案为：‎ ‎　‎ ‎16．（4分）（2015•泉州）如图，在⊙O的内接四边形ABCD中，点E在DC的延长线上．若∠A=50°，则∠BCE=　50°　．‎ 解：∵四边形ABCD内接于⊙O，‎ ‎∴∠BCE=∠A=50°．‎ 故答案为50°．‎ ‎　‎ ‎17．（4分）（2015•泉州）在以O为圆心3cm为半径的圆周上，依次有A、B、C三个点，若四边形OABC为菱形，则该菱形的边长等于　3　cm；弦AC所对的弧长等于　2π或4π　cm．‎ 解：连接OB和AC交于点D，‎ ‎∵四边形OABC为菱形，‎ ‎∴OA=AB=BC=OC，‎ ‎∵⊙O半径为3cm，‎ ‎∴OA=OC=3cm，‎ ‎∵OA=OB，‎ ‎∴△OAB为等边三角形，‎ ‎∴∠AOB=60°，‎ ‎∴∠AOC=120°，‎ ‎∴==2π，‎ ‎∴优弧==4π，‎ 故答案为3，2π或4π．‎ ‎　‎ 三、解答题（共9小题，满分89分）‎ ‎18．（9分）（2015•泉州）计算：|﹣4|+（2﹣π）0﹣8×4﹣1+÷．‎ 解：原式=4+1﹣2+3=6．‎ ‎19．（9分）（2015•泉州）先化简，再求值：（x﹣2）（x+2）+x2（x﹣1），其中x=﹣1．‎ 解：原式=x2﹣4+x3﹣x2=x3﹣4，‎ 当x=﹣1时，原式=﹣5．‎ ‎　‎ ‎20．（9分）（2015•泉州）如图，在矩形ABCD中．点O在边AB上，∠AOC=∠BOD．求证：AO=OB．‎ 解：∵四边形ABCD是矩形，‎ ‎∴∠A=∠B=90°，AD=BC，‎ ‎∵∠AOC=∠BOD，‎ ‎∴∠AOC﹣∠DOC=∠BOD﹣∠DOC，‎ ‎∴∠AOD=∠BOC，‎ 在△AOD和△BOC中，‎ ‎，‎ ‎∴△AOD≌△BOC，‎ ‎∴AO=OB．‎ ‎　‎ ‎21．（9分）（2015•泉州）为弘扬“东亚文化”，某单位开展了“东亚文化之都”演讲比赛，在安排1位女选手和3位男选手的出场顺序时，采用随机抽签方式．‎ ‎（1）请直接写出第一位出场是女选手的概率；‎ ‎（2）请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果，并求出他们都是男选手的概率．‎ 解：（1）P（第一位出场是女选手）=；‎ ‎（2）列表得：‎ 女 男 男 男 女 ‎﹣﹣﹣‎ ‎（男，女）‎ ‎（男，女）‎ ‎（男，女）‎ 男 ‎（女，男）‎ ‎﹣﹣﹣‎ ‎（男，男）‎ ‎（男，男）‎ 男 ‎（女，男）‎ ‎（男，男）‎ ‎﹣﹣﹣‎ ‎（男，男）‎ 男 ‎（女，男）‎ ‎（男，男）‎ ‎（男，男）‎ ‎﹣﹣﹣‎ 所有等可能的情况有12种，其中第一、二位出场都是男选手的情况有6种，‎ 则P（第一、二位出场都是男选手）==．‎ ‎　‎ ‎22．（9分）（2015•泉州）清明期间，某校师生组成200个小组参加“保护环境，美化家园”植树活动．综合实际情况，校方要求每小组植树量为2至5棵，活动结束后，校方随机抽查了其中50个小组，根据他们的植树量绘制出如图所示的两幅不完整统计图．请根据图中提供的信息，解答下面的问题：‎ ‎（1）请把条形统计图补充完整，并算出扇形统计图中，植树量为“5棵树”的圆心角是　72　°．‎ ‎（2）请你帮学校估算此次活动共种多少棵树．‎ 解：（1）植树量为“5棵树”的圆心角是：360°×=72°，‎ 故答案是：72；‎ ‎（2）每个小组的植树棵树：（2×8+3×15+4×17+5×10）=（棵），‎ 则此次活动植树的总棵树是：×200=716（棵）．‎ 答：此次活动约植树716棵．‎ ‎　‎ ‎23．（9分）（2015•泉州）如图，在平面直角坐标系中，点A（，1）、B（2，0）、O（0，0），反比例函数y=图象经过点A．‎ ‎（1）求k的值；‎ ‎（2）将△AOB绕点O逆时针旋转60°，得到△COD，其中点A与点C对应，试判断点D是否在该反比例函数的图象上？‎ 解：（1）∵函数y=的图象过点A（，1），‎ ‎∴k=xy=×1=；‎ ‎（2）∵B（2，0），‎ ‎∴OB=2，‎ ‎∵△AOB绕点O逆时针旋转60°得到△COD，‎ ‎∴OD=OB=2，∠BOD=60°，‎ 如图，过点D作DE⊥x轴于点E，‎ DE=OE•sin60°=2×=，‎ OE=OD•cos60°=2×=1，‎ ‎∴D（1，），‎ 由（1）可知y=，‎ ‎∴当x=1时，y==，‎ ‎∴D（1，）在反比例函数y=的图象上．‎ ‎　‎ ‎24．（9分）（2015•泉州）某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的而积最大？下面是两位学生争议的情境：‎ 请根据上面的信息，解决问题：‎ ‎（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；‎ ‎（2）请你判断谁的说法正确，为什么？‎ 解：（1）设AB=x米，可得BC=69+3﹣2x=72﹣2x；‎ ‎（2）小英说法正确；‎ 矩形面积S=x（72﹣2x）=﹣2（x﹣18）2+648，‎ ‎∵72﹣2x＞0，‎ ‎∴x＜36，‎ ‎∴0＜x＜36，‎ ‎∴当x=18时，S取最大值，‎ 此时x≠72﹣2x，‎ ‎∴面积最大的表示正方形．‎ ‎　‎ ‎25．（13分）（2015•泉州）（1）如图1是某个多面体的表面展开图．‎ ‎①请你写出这个多面体的名称，并指出图中哪三个字母表示多面体的同一点；‎ ‎②如果沿BC、GH将展开图剪成三块，恰好拼成一个矩形，那么△BMC应满足什么条件？（不必说理）‎ ‎（2）如果将一个三棱柱的表面展开图剪成四块，恰好拼成一个三角形，如图2，那么该三棱柱的侧面积与表面积的比值是多少？为什么？（注：以上剪拼中所有接缝均忽略不计）‎ 解：（1）①根据这个多面体的表面展开图，可得 这个多面体是直三棱柱，‎ 点A、M、D三个字母表示多面体的同一点．‎ ‎②△BMC应满足的条件是：‎ a、∠BMC=90°，且BM=DH，或CM=DH；‎ b、∠MBC=90°，且BM=DH，或BC=DH；‎ c、∠BCM=90°，且BC=DH，或CM=DH；‎ ‎（2）如图2，连接AB、BC、CA，，‎ ‎∵△DEF是由一个三棱柱表面展开图剪拼而成，‎ ‎∴矩形ACKL、BIJC、AGHB为棱柱的三个侧面，‎ 且四边形DGAL、EIBH、FKCJ须拼成与底面△ABC全等的另一个底面的三角形，‎ ‎∴AC=LK，且AC=DL+FK，‎ ‎∴，‎ 同理，可得 ‎，‎ ‎∴△ABC∽△DEF，‎ ‎∴，‎ 即S△DEF=4S△ABC，‎ ‎∴，‎ 即该三棱柱的侧面积与表面积的比值是．‎ ‎　‎ ‎26．（13分）（2015•泉州）阅读理解 抛物线y=x2上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．‎ 问题解决 如图，在平面直角坐标系中，直线y=kx+1与y轴交于C点，与函数y=x2的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．‎ ‎（1）写出点C的坐标，并说明∠ECF=90°；‎ ‎（2）在△PEF中，M为EF中点，P为动点．‎ ‎①求证：PE2+PF2=2（PM2+EM2）；‎ ‎②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．‎ 解：（1）当x=0时，y=k•0+1=1，‎ 则点C的坐标为（0，1）．‎ 根据题意可得：AC=AE，‎ ‎∴∠AEC=∠ACE．‎ ‎∵AE⊥EF，CO⊥EF，‎ ‎∴AE∥CO，‎ ‎∴∠AEC=∠OCE，‎ ‎∴∠ACE=∠OCE．‎ 同理可得：∠OCF=∠BCF．‎ ‎∵∠ACE+∠OCE+∠OCF+∠BCF=180°，‎ ‎∴2∠OCE+2∠OCF=180°，‎ ‎∴∠OCE+∠OCF=90°，即∠ECF=90°；‎ ‎（2）①过点P作PH⊥EF于H，‎ Ⅰ．若点H在线段EF上，如图2①．‎ ‎∵M为EF中点，‎ ‎∴EM=FM=EF．‎ 根据勾股定理可得：‎ PE2+PF2﹣2PM2=PH2+EH2+PH2+HF2﹣2PM2‎ ‎=2PH2+EH2+HF2﹣2（PH2+MH2）‎ ‎=EH2﹣MH2+HF2﹣MH2‎ ‎=（EH+MH）（EH﹣MH）+（HF+MH）（HF﹣MH）‎ ‎=EM（EH+MH）+MF（HF﹣MH）‎ ‎=EM（EH+MH）+EM（HF﹣MH）‎ ‎=EM（EH+MH+HF﹣MH）‎ ‎=EM•EF=2EM2，‎ ‎∴PE2+PF2=2（PM2+EM2）；‎ Ⅱ．若点H在线段EF的延长线（或反向延长线）上，如图2②．‎ 同理可得：PE2+PF2=2（PM2+EM2）．‎ 综上所述：当点H在直线EF上时，都有PE2+PF2=2（PM2+EM2）；‎ ‎②连接CD、PM，如图3．‎ ‎∵∠ECF=90°，‎ ‎∴▱CEDF是矩形，‎ ‎∵M是EF的中点，‎ ‎∴M是CD的中点，且MC=EM．‎ 由①中的结论可得：‎ 在△PEF中，有PE2+PF2=2（PM2+EM2），‎ 在△PCD中，有PC2+PD2=2（PM2+CM2）．‎ ‎∵MC=EM，‎ ‎∴PC2+PD2=PE2+PF2．‎ ‎∵PE=PF=3，‎ ‎∴PC2+PD2=18．‎ ‎∵1＜PD＜2，‎ ‎∴1＜PD2＜4，‎ ‎∴1＜18﹣PC2＜4，‎ ‎∴14＜PC2＜17．‎ ‎∵PC＞0，‎ ‎∴＜PC＜．‎ ‎　‎