2010年浙江省东阳县中考数学试卷及答案

2010年浙江省东阳县中考数学试卷及答案

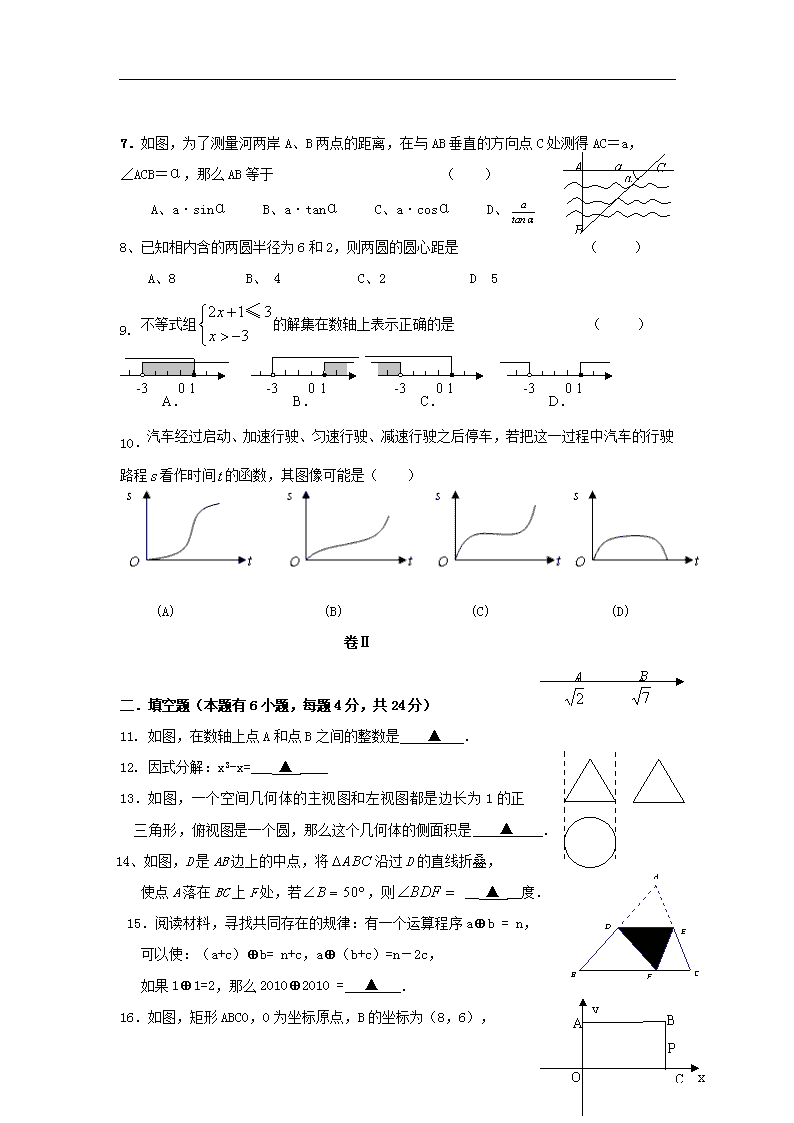
‎2010年浙江省东阳初中毕业生学业水平考试数学试卷 说明：‎ ‎1。全卷分卷Ⅰ和卷Ⅱ两部分，共三大题24小题，满分为120分。考试时间为100分钟。‎ ‎2．必须全部在答卷纸上作答，做在试卷上无效。卷Ⅰ的答案必须用2B铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔答在答题纸的相应位置上。‎ ‎3．请用黑色字迹钢笔或签字笔在答题纸上填写姓名和准考证号码。‎ ‎4．作图时，可先用2B铅笔，确定后必须使用黑色字迹钢笔或签字笔涂黑。 ‎ 卷Ⅰ 说明：本卷共有1大题，10小题，共30分，请用2B铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满。‎ 一．选择题（本题有10小题，每题3分，共30分）‎ ‎ 1. 是 ( )‎ A．无理数 B．有理数 C．整数 D．负数 ‎ ‎2.某电视台报道，截止到‎2010年5月5日，慈善总会已接受支援玉树地震灾区的捐款 ‎15510000元．将15510000用科学记数法表示为 ( )‎ ‎ A. B. C. D.‎ ‎3.某反比例函数的图象经过点(-2,3)，则此函数图象也经过点 （ ）‎ A．(2,-3) B．(-3,-3) C．（2，3） D．（-4，6）‎ ‎4.已知等腰三角形的一个内角为，则这个等腰三角形的顶角为 （ ）‎ A. B. C.或 D.或 ‎5.使分式有意义，则的取值范围是 （ ）‎ A. B. C. D. ‎ ‎6. 张家界国际乡村音乐周活动中，来自中、日、美的三名音乐家准备在同一节目中依次演奏本国的民族音乐，若他们出场先后的机会是均等的，则按“美—日—中”顺序演奏的概率是 （ ）‎ ‎ A、 B、 C、 D ‎ ‎ ‎ ‎7．如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向点C处测得AC＝a，‎ ‎∠ACB＝α，那么AB等于 （ ）‎ A B C a α A、a·sinα B、a·tanα C、a·cosα D、‎ ‎8、已知相内含的两圆半径为6和2，则两圆的圆心距是 （ ）‎ ‎ A、8 B、 4 C、2 D 5‎ ‎9. 不等式组的解集在数轴上表示正确的是 （ ）‎ ‎-3‎ ‎1‎ ‎0‎ A．‎ ‎-3‎ ‎1‎ ‎0‎ B．‎ ‎-3‎ ‎1‎ ‎0‎ C．‎ ‎-3‎ ‎1‎ ‎0‎ D．‎ ‎10．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程看作时间的函数，其图像可能是（ ）‎ ‎ (A) (B) (C) (D)‎ 卷Ⅱ ‎ ‎ A B 二．填空题（本题有6小题，每题4分，共24分）‎ ‎11. 如图，在数轴上点A和点B之间的整数是 ▲ ．‎ ‎12. 因式分解：x3-x=___ ▲ ____‎ ‎13．如图，一个空间几何体的主视图和左视图都是边长为1的正 三角形，俯视图是一个圆，那么这个几何体的侧面积是 ▲ ． ‎ ‎14、如图，D是AB边上的中点，将沿过D的直线折叠，‎ 使点A落在BC上F处，若，则 __ ▲ __度． ‎ ‎ 15．阅读材料，寻找共同存在的规律：有一个运算程序a⊕b = n，‎ 可以使：（a+c）⊕b= n+c，a⊕（b+c）=n－2c，‎ A B O C x y P 如果1⊕1=2，那么2010⊕2010 = ▲ ．‎ ‎16．如图，矩形ABCO，O为坐标原点，B的坐标为（8，6），‎ A、C分别在坐标轴上，P是线段BC上动点，设PC＝m，已 知点D在第一象限，且是两直线y1＝2x＋6、y2＝2x－6中某 条上的一点，若△APD是等腰Rt△，则点D的坐标为 ▲ ‎ 三．解答题（本题有8小题，共66分）‎ A B C D F E ‎17（6分）计算： ‎ ‎18（6分）如图，已知BE⊥AD，CF⊥AD，且BE＝CF．‎ （1） 请你判断AD是△ABC的中线还是角平分线？请证明 你的结论．‎ ‎（2）连接BF、CE，若四边形BFCE是菱形，则△ABC中应 添加一个条件 ▲ ‎ Ｐ ‎19（6分）在如图的方格纸中，每个小方格都是边长为1个单位的正方形，的三个顶点 都在格点上（每个小方格的顶点叫格点）．‎ ‎（1）如果建立直角坐标系，使点B的坐标为（－5，2），点C的坐标为（－2，2），则点A的坐标为 ▲ ； ‎ ‎(2) 画出绕点Ｐ顺时针旋转后的△Ａ１Ｂ１Ｃ１，并求线段BC扫过的面积.‎ ‎20（8分）如图，BD为⊙O的直径，点A是弧BC的中点，AD交BC于E点，AE=2，ED=4. ‎ ‎（1）求证: ～；‎ ‎(2) 求的值； ‎ ‎（3）延长BC至F，连接FD，使的面积等于，‎ 求的度数.‎ ‎21（8分）如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出（在轴上），运动员乙在距点6米的处发现球在自己头的正上方达到最高点 ‎，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．‎ ‎（1）求足球开始飞出到第一次落地时，该 抛物线的表达式．‎ ‎（2）足球第一次落地点距守门员多少 米？（取）‎ ‎（3）运动员乙要抢到第二个落点，他应 再向前跑多少米？（取）‎ ‎22（10分）我市中考体育测试中，1分钟跳绳为自选项目．某中学九年级共有50名女同学选考1分钟跳绳，根据测试评分标准，将她们的成绩进行统计后分为四等，并绘制成下面的频数分布表（注：6~7的意义为大于等于6分且小于7分，其余类似）和扇形统计图（如图）．‎ 频数分布表 等级 分值 跳绳（次/1分钟）‎ 扇形统计图 A C D B64%‎ 频数 A ‎9~10‎ ‎150~170‎ ‎4‎ ‎8~9‎ ‎140~150‎ ‎12‎ B ‎7~8‎ ‎130~140‎ ‎17‎ ‎6~7‎ ‎120~130‎ m C ‎5~6‎ ‎110~120‎ ‎0‎ ‎4~5‎ ‎90~110‎ n D ‎3~4‎ ‎70~90‎ ‎1‎ ‎0~3‎ ‎0~70‎ ‎0‎ ‎（1）等级A人数的百分比是 ▲ ；‎ ‎（2）求的值；‎ ‎（3）在抽取的这个样本中，请说明哪个分数段的学生最多？‎ 请你帮助老师计算这次1分钟跳绳测试的及格率（6分以上含6分为及格）．‎ ‎23（10分）如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸。A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元。‎ 探究1：如果木板边长为2米，FC＝1米，则一块木板用墙纸的费用需 ▲ 元；‎ 探究2：如果木板边长为1米，求一块木板需用墙纸的最省费用；‎ 探究3：设木板的边长为a（a为整数），当正方形 EFCG的边长为多少时？墙纸费用最省；如要用这 样的多块木板贴一堵墙（7×3平方米）进行装饰，‎ 要求每块木板A型的墙纸不超过1平方米，且尽量 不浪费材料，则需要这样的木板 ▲ 块。‎ C O A B D N M P x y R H ‎24（12分）如图，P为正方形ABCD的对称中心，A（0，3），B（1，0），直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以个单位每秒速度运动，运动时间为t。求：‎ ‎（1）C的坐标为 ▲ ；‎ ‎（2）当t为何值时，△ANO与△DMR相似？‎ ‎（3）△HCR面积S与t的函数关系式；‎ 并求以A、B、C、R为顶点的四边形是梯形 时t的值及S的最大值。‎ 学校 班级 姓名 序号 九年级数学答题卷 试卷 I（一、选择题 ，本题有10小题，每小题3分，共30分）‎ 试卷 Ⅱ（二、填空题 ，本题有6小题，每小题4分，共24分）‎ 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 ‎11._____________； 12._____________； 13._____________；‎ ‎14._____________； 15._____________； 16._______ ______.‎ A B C D F E ‎（1）证明 ‎（2） ‎ ‎17、（本题6分）计算：‎ A B C D E F M ‎18.(本题6分)‎ ‎(1)‎ ‎17.(本题6分)‎ P ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎（1） ‎ ‎(2)‎ ‎ ‎ 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 ‎21.(本题8分)‎ ‎20.(本题8分)‎ ‎19.(本题6分)‎ 扇形统计图 A C D B64%‎ ‎（1） ‎ ‎（2）‎ ‎（3）‎ ‎ ‎ ‎（1） ‎ ‎（2）‎ ‎（3）‎ 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 ‎23.(本题10分)‎ ‎22.(本题10分)‎ C O A B D N M P x y C O A B D N M P x y ‎（1） ‎ ‎（2）‎ ‎（3）‎ C O A B D N M P x y R H 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 ‎24.(本题12分)‎ 请在各题目的区域内作答，超出黑色矩形边框限定区域内的答案无效 参考答案 一、选择题：（每题3分，共30分）‎ ‎1‎ ‎2‎ ‎3 ‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ B C A C D A B C A A 二、填空题：（每题4分，共24分）‎ ‎11. 2 12. x(x+1)(x-1) 13. 14. 80°‎ ‎15. -2007 16. (4,2),(4,14),(,),(,)‎ 三、解答题：‎ ‎17．=-3+2+1-1．．．．．．．．．．．．．．．．．．．．．．４分 ‎=-１．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 ‎18. （1）AD是△ABC的中线.．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 理由如下：∵ＢＥ⊥ＡＤ，ＣＦ⊥ＡＤ，∴∠ＢＥＤ＝∠ＣＦＤ＝９０°．．．．．．．．．．．１分 又∵ＢＥ＝ＣＦ，∠ＢＤＥ＝∠ＣＦＤ　∴△ＢＤＥ≌△ＣＦＤ（ＡＡＳ）．．．．．．．．．２分 ‎（２）ＡＢ＝ＡＣ或∠ＡＢＣ＝∠ＡＣＢ或ＡＤ⊥ＢＣ或ＡＤ平分∠ＢＡＣ．．．．．．．．．２分 ‎１９．（１）Ａ（－４，４）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分　　‎ ‎（２）图略．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 线段BC扫过的面积＝（４２－１２）＝．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 ‎２０．（１）∵点A是弧BC的中点　∴∠ＡＢＣ＝∠ＡＤＢ 又∵∠ＢＡＥ＝∠ＢＡＥ　　∴△ＡＢＥ∽△ＡＢＤ．．．．．．．．．．．．．．．．．．．．．．．．．．．３分 ‎（２）∵△ＡＢＥ∽△ＡＢＤ　∴ＡＢ２＝２×６＝１２　∴ＡＢ＝２‎ 在Ｒｔ△ＡＤＢ中，ｔａｎ∠ＡＤＢ＝．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．３分 ‎（３）连接ＣＤ，可得ＢＦ＝８，ＢＥ＝４，则ＥＦ＝４，△ＤＥＦ是正三角形，‎ ‎∠ＥＤＦ＝６０°．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 ‎21、（1）y=－ （3分）‎ ‎ （2）y=0, x=6+4︽13………………………………………………………………2分 ‎ （3）设y= m=13+2︽18‎ ‎ y=0, x=18±2︽23 ∴ 再向前跑10米…………………………………3分 ‎２２．解：（1）32%……………………………………………………………………………2分 ‎（2）根据题意，得；．‎ 则 解之，得…………………………………………………………………………4分 ‎（3）7~8分数段的学生最多…… ……………………………………………………2分 及格人数（人），及格率 答：这次1分钟跳绳测试的及格率为．…………………………………………2分 ‎……………………………………………………………………………… 2分 ‎（2）y=20x2—20x+60 ……………………………………………………………………2分 当x=时，y小=55元。…………………………………………………………………1分 ‎（3）y=20x2—20ax+60a2 …………………………………………………………………2分 ‎ 当x=a时，…………………………………………………………………………1分 ‎21块 …………………………………………………………………………………2分 ‎24．（1）Ｃ（４，１）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 ‎（2）当∠MDR＝45０时，ｔ＝2,点Ｈ（2，0）．．．．．．．．．．．．．．．．．．．．．．．．．２分 当∠DRM＝45０时，ｔ＝3,点Ｈ（3，0）．．．．．．．．．．．．．．．．．．．．．．．．．． ２分 ‎（３）Ｓ＝－ｔ２＋２ｔ（０＜ｔ≤４）；（1分）Ｓ＝ｔ２－２ｔ（ｔ＞４）（1分）‎ 当ＣＲ∥ＡＢ时，ｔ＝，（1分） Ｓ＝ （1分）‎ 当ＡＲ∥ＢＣ时，ｔ＝， Ｓ＝ （1分）‎ 当ＢＲ∥ＡＣ时，ｔ＝， Ｓ＝ （1分）‎