五年级上册数学教案-5平行四边形的面积 ▏沪教版 (1)

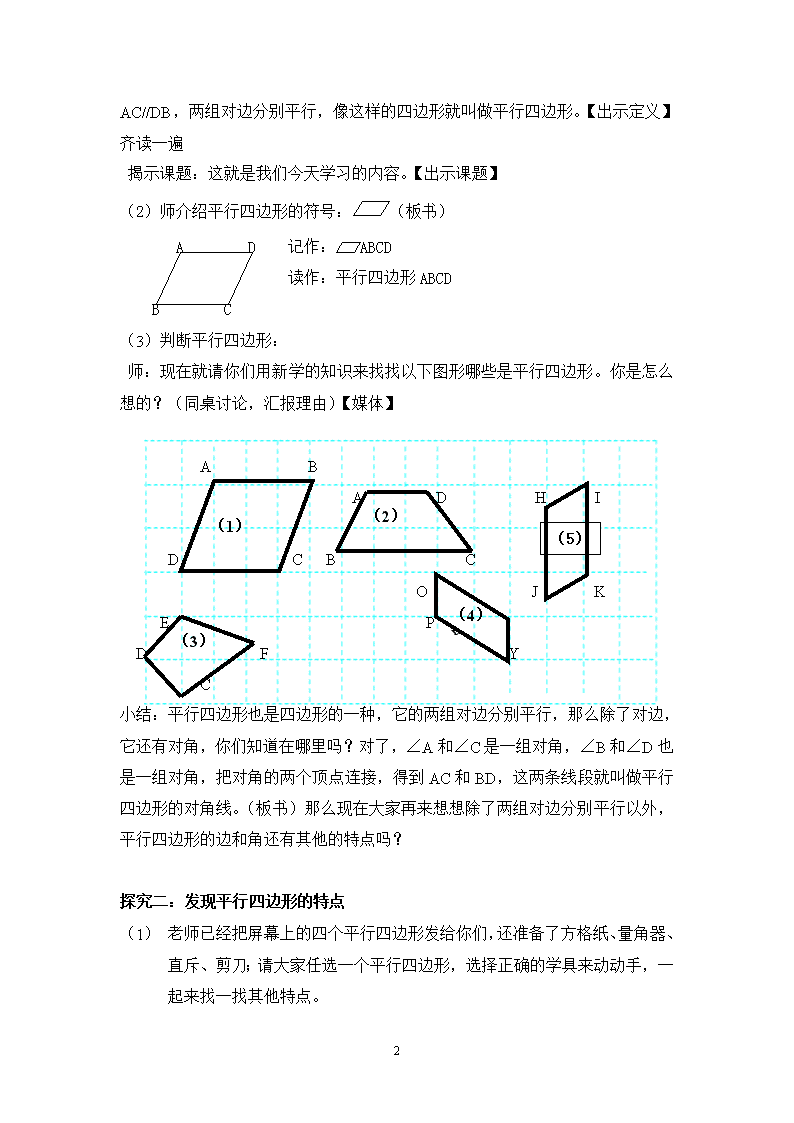
五年级上册数学教案-5平行四边形的面积 ▏沪教版 (1)

教学内容：P55平行四边形 ‎ 教学目标：‎ ‎1、认识平行四边形，知道它的特征。‎ ‎2、体会平行四边形、长方形之间的关系。‎ ‎3、通过动手操作发现平行四边形的某些特性，以此培养学生的归纳、总结的能力。‎ 教学重点：‎ 知道平行四边形的特征 教学难点：‎ 能正确判断哪些图形是平行四边形 教学具准备：‎ 红蓝色带、图形拼版、小棒 教学过程：‎ 一、引入 ‎1、出示红蓝色带 ‎（1）师：看，这两条色带是什么图形？你知道长方形有什么特点？‎ 生：长方形的对边平行且相等，长方形的四个角都是90°。‎ ‎（2）师：看，老师把这两条长方形的色带中间部分像这样放在一起，这叫做交叠。【手势】现在请你们也像老师这样放，看看两条色带中间交叠的部分，会得到什么图形？‎ ‎（生尝试后汇报）请你上来摆一摆，并说说色带中间交叠部分是什么图形？‎ 生：垂直交叠，得到长方形；斜着交叠得到四边形。（2人）‎ 师：是啊，你们用2条色带中间部分交叠出了一些四边形，【媒体】‎ 二、新授 探究一：初步认识平行四边形 ‎（1）师：长方形也是四边形的一种，我们已经学过了（隐去），那么今天我们就来研究其余的四边形。我们标上字母，仔细观察，它们有什么共同的特点呢？‎ 生1：我发现这两组边是互相平行的，因为色带的对边是互相平行的。（2人）‎ 生2：我发现都是AB平行于CD，AC平行于BD。‎ 板书： A C AB//CD AC//DB B D 师：老师把这个四边形截取一个到黑板上，同学们都发现了AB//CD ‎ 4‎ ‎ AC//DB，两组对边分别平行，像这样的四边形就叫做平行四边形。【出示定义】齐读一遍 揭示课题：这就是我们今天学习的内容。【出示课题】‎ ‎（2）师介绍平行四边形的符号： （板书）‎ ‎ A D 记作： ABCD 读作：平行四边形ABCD ‎ B C ‎ ‎（3）判断平行四边形：‎ ‎ 师：现在就请你们用新学的知识来找找以下图形哪些是平行四边形。你是怎么想的？（同桌讨论，汇报理由）【媒体】‎ ‎ A B ‎（2）‎ ‎ A D H I ‎（5）‎ ‎（1）‎ ‎ D C B C ‎（4） X ‎ O J K ‎（3）‎ ‎ E P ‎ D F Y ‎ C 小结：平行四边形也是四边形的一种，它的两组对边分别平行，那么除了对边，它还有对角，你们知道在哪里吗？对了，∠A和∠C是一组对角，∠B和∠D也是一组对角，把对角的两个顶点连接，得到AC和BD，这两条线段就叫做平行四边形的对角线。（板书）那么现在大家再来想想除了两组对边分别平行以外，平行四边形的边和角还有其他的特点吗？‎ 探究二：发现平行四边形的特点 （1） 老师已经把屏幕上的四个平行四边形发给你们，还准备了方格纸、量角器、直斥、剪刀；请大家任选一个平行四边形，选择正确的学具来动动手，一起来找一找其他特点。‎ 4‎ ‎（2）交流 生1：对边相等，可以用尺量；‎ ‎ 我沿着这条线，剪开来，重叠之后发现对边是相等的。（2人）‎ 生2：对角相等，用量角器量出来的；或者剪下来重叠的。‎ 师：【媒体出示剪，重叠的方法】刚才同学们用量一量的方法发现了平行四边形的对边相等，对角也相等。【板书：对角相等】【板书：对边相等】‎ ‎（3）巩固练习 选择（在方格图）‎ ‎1、（实物投影）出示梯形，和一个正方形，三角形和小的三角形 问：几号图形可以和梯形拼成平行四边形？（演示证明）‎ 小结：真棒!你们已经会根据平行四边形的特点来观察了。‎ ‎2、出示一个直角三角形，和相同的直角三角形，小三角形，梯形 几号图形可以和三角形拼成平行四边形？‎ 要求：先观察，再动手拼拼。‎ 小结：2个完全相同的三角形可以拼出3种不同的平行四边形。‎ 探究三：平行四边形，长方形，正方形之间的关系 师：当他们的斜边重合时，这是一个什么图形啊？它是平行四边形吗？‎ 可以摆出长方形观察，你还有其他想法吗？‎ 小结：正方形和长方形具有平行四边形的所有特征，所以正方形和长方形是特殊的平行四边形。（请学生来填这个集合图）‎ ‎ ‎ ‎ 正方形 三、 练习 练习一：小实验：书上57页到58页。‎ 三角形的三条边确定了，它的形状大小就完全确定了。‎ 平行四边形尽管边确定了，但他的形状大小还不能完全确定。【老师演示可变动的平行四边形】‎ 4‎ 练习二：生活中的平行四边形 ‎ 如此特别的平行四边形在生活中也被广泛应用，我们一起来看一看【媒体】，你找到平行四边形了吗？‎ 练习三：练习：‎ 木匠张师傅想把一块平行四边形的木板锯成两部分，拼成一张长方形桌面，假如你是张师傅，该怎么锯呢？想试试吗？找一张平行四边形的纸试一试 。‎ 四、小结 你有哪些收获？‎ 五、作业 练习册、‎ 板书设计：‎ 平行四边形 像这样两组对边分别平行的四边形就叫做平行四边形。‎ AB//CD AC//DB ‎ 记作： ABCD 读作：平行四边形ABCD ‎ 对角线AC、BD 特点：对角相等、对边相等 4‎