弧长及扇形的面积说课教案

弧长及扇形的面积说课教案

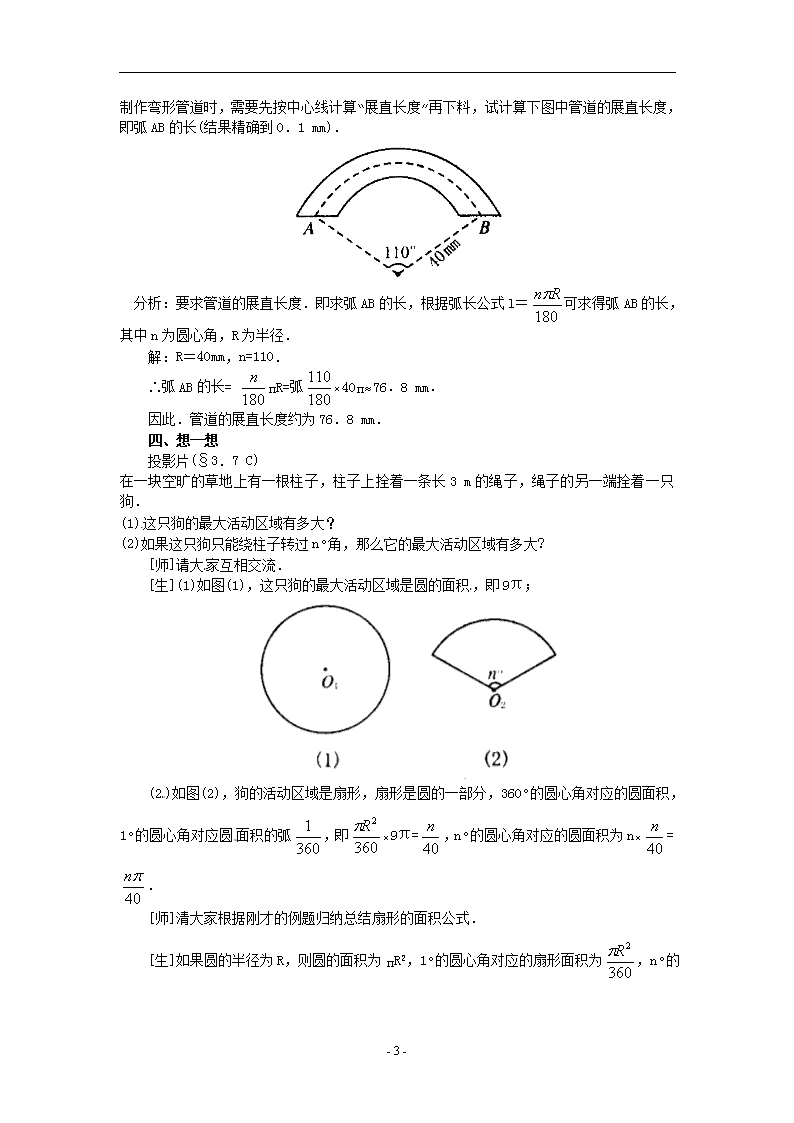
‎§3．7 弧长及扇形的面积 课时安排 1课时 从容说课 ‎ 本节课的内容为弧长及扇形的面积，是在学习了圆的有关性质后，利用圆的性质探索推导弧长及扇形的面积，并能运用得出的结论进行有关计算，实质上是圆的有关性质的运用．本节的重点和难点是学生自己能推导并掌握弧长及扇形的面积，并能应用公式解决问题．‎ ‎ 在教学中，教师不要急于给出学生公式，而要引导学生自己根据已有的知识推导公式．如果学生有困难，可以采取小组合作的形式解决．这样既能使学生有成就感，又能培养他们的探索能力，还能使所学知识掌握得比较牢固，那么运用公式进行计算来解决问题就比较容易了．‎ ‎ 课 题 ‎ § 3．7 弧长及扇形的面积 ‎ 教学目标 ‎ (一)教学知识点 ‎ 1．经历探索弧长计算公式及扇形面积计算公式的过程；‎ ‎ 2．了解弧长计算公式及扇形面积计算公式，并会应用公式解决问题．‎ ‎ (二)能力训练要求 ‎ 1．经历探索弧长计算公式及扇形面积计算公式的过程，培养学生的探索能力．‎ ‎ 2．了解弧长及扇形面积公式后，能用公式解决问题，训练学生的数学运用能力．‎ ‎ (三)情感与价值观要求 ‎ 1．经历探索弧长及扇形面积计算公式．让学生体验教学活动充满着探索与创造，感受数学的严谨性以及数学结论的确定性．‎ ‎ 2．通过用弧长及扇形面积公式解决实际问题．让学生体验数学与人类生活的密切联系，激发学生学习数学的兴趣，提高他们的学习积极性，同时提高大家的运用能力．‎ 教学重点 ‎ 1．经历探索弧长及扇形面积计算公式的过程．‎ ‎ 2．了解弧长及扇形面积计算公式．‎ ‎ 3．会用公式解决问题．‎ ‎ 教学难点 ‎ 1．探索弧长及扇形面积计算公式．‎ ‎ 2．用公式解决实际问题．‎ 教学方法 ‎ 学生互相交流探索法 教具准备 ‎ 2．投影片四张 ‎ 第一张：(记作§ 3．7 A)‎ ‎ 第二张：(记作§ 3．7 B)‎ ‎ 第三张：(记作§ 3．7 C)‎ ‎ 第四张：(记作§ 3．7 D)‎ ‎ 教学过程 ‎ Ⅰ．创设问题情境，引入新课 ‎ ‎ - 6 -‎ ‎ [师]在小学我们已经学习过有关圆的周长和面积公式，弧是圆周的一部分，扇形是圆的—部分，那么弧长与扇形面积应怎样计算?它们与圆的周长、圆的面积之间有怎样的关系呢?本节课我们将进行探索．‎ ‎ Ⅱ．新课讲解 ‎ 一、复习 ‎ 1．圆的周长如何汁算?‎ ‎ 2，圆的面积如何计算?‎ ‎ 3．圆的圆心角是多少度?‎ ‎ [生]若圆的半径为r，则周长l＝2πr，面积S＝πr2，圆的圆心角是360°．‎ ‎ 二、探索弧长的计算公式 投影片(§ 3．7 A)‎ ‎ 如图，某传送带的一个转动轮的半径为10cm ‎．‎ ‎ (1)转动轮转一周，传送带上的物品A被传送多少厘米?‎ ‎ (2)转动轮转1°，传送带上的物品A被传送多少厘米?‎ ‎ (3)转动轮转n°，传送带上的物品A被传送多少厘米?‎ ‎ [师]分析：转动轮转一周，传送带上的物品应被传送一个圆的周长；因为圆的周长对应360°的圆心角，所以转动轮转1°，传送带上的物品A被传送圆周长的；转动轮转n°，传送带上的物品A被传送转l°时传送距离的n倍．‎ ‎ [生]解：(1)转动轮转一周．传送带上的物品A被传送2π×10＝20πcm；‎ ‎ (2)转动轮转1°，传送带上的物品A被传送cm；‎ ‎ (3)转动轮转n°，传送带上的物品A被传送n×cm．‎ ‎ [师]根据上面的计算，你能猜想出在半径为R的圆中，n°的圆心角所对的弧长的计算公式吗?请大家互相交流．‎ ‎ [生]根据刚才的讨论可知，360°的圆心角对应圆周长2πR，那么1°的圆心角对应的弧长为，n°的圆心角对应的弧长应为1°的圆心角对应的弧长的n倍，即n×.‎ ‎ [师]表述得非常棒．‎ 在半径为R的圆中，n°的圆心角所对的弧长(arclength)的计算公式为： ‎ ‎ l=.‎ ‎ 下面我们看弧长公式的运用．‎ ‎ 三、例题讲解 投影片(§3．7 B)‎ - 6 -‎ 制作弯形管道时，需要先按中心线计算“展直长度”再下料，试计算下图中管道的展直长度，即弧AB的长(结果精确到0．1 mm)．‎ ‎ 分析：要求管道的展直长度．即求弧AB的长，根据弧长公式l＝可求得弧AB的长，其中n为圆心角，R为半径．‎ ‎ 解：R＝40mm，n=110．‎ ‎ ∴弧AB的长= πR=弧×40π≈76．8 mm．‎ ‎ 因此．管道的展直长度约为76．8 mm．‎ ‎ 四、想一想 ‎ ‎ 投影片(§3．7 C)‎ 在一块空旷的草地上有一根柱子，柱子上拴着一条长3 m的绳子，绳子的另一端拴着一只狗．‎ ‎(1)这只狗的最大活动区域有多大？‎ ‎(2)如果这只狗只能绕柱子转过n°角，那么它的最大活动区域有多大?‎ ‎ [师]请大家互相交流．‎ ‎[生](1)如图(1)，这只狗的最大活动区域是圆的面积，即9π；‎ ‎ (2)如图(2)，狗的活动区域是扇形，扇形是圆的一部分，360°的圆心角对应的圆面积，1°的圆心角对应圆面积的弧，即×9π=，n°的圆心角对应的圆面积为n×=．‎ ‎ [师]清大家根据刚才的例题归纳总结扇形的面积公式．‎ ‎ [生]如果圆的半径为R，则圆的面积为πR2，1°的圆心角对应的扇形面积为 - 6 -‎ ‎，n°的圆心角对应的扇形面积为n·=．因此扇形面积的计算公式为S扇形＝πR2，‎ 其中R为扇形的半径，n为圆心角．‎ ‎ 五、弧长与扇形面积的关系 ‎ [师]我们探讨了弧长和扇形面积的公式，在半径为R的圆中，n°的圆心角所对的弧长的计算公式为l＝πR，n°的圆心角的扇形面积公式为S扇形＝πR2，在这两个公式中，弧长和扇形面积都和圆心角n．半径R有关系，因此l和S之间也有一定的关系，你能猜得出吗?请大家互相交流．‎ ‎ [生]∵l=πR，S扇形=πR2，‎ ‎ ∴πR2=R·πR．∴S扇形=lR．‎ ‎ 六、扇形面积的应用 ‎ 投影片(§3．7 D)‎ 扇形AOB的半径为12 cm，∠AOB＝120°，求弧AB的长(结果精确到0．1 cm)和扇形AOB的面积(结果精确到0．1 cm2)‎ ‎ 分析：要求弧长和扇形面积，根据公式需要知道半径尺和圆心角n即可，本题中这些 条件已经告诉了，因此这个问题就解决了．‎ ‎ 解：弧AB的长=π×12≈25．1cm：‎ ‎ S扇形=π×122≈150．7 cm2．‎ ‎ 因此，弧AB的长约为25．1 cm，扇形AOB的面积约为150．7 cm2．‎ ‎ Ⅲ．课堂练习 ‎ 随堂练习 ‎ Ⅳ．课时小结 ‎ 本节课学习了如下内容：‎ ‎ 1．探索弧长的计算公式l＝πR，并运用公式进行计算；‎ ‎ 2．探索扇形的面积公式S＝πR2，并运用公式进行计算；‎ ‎ 3．探索弧长l及扇形的面积S之间的关系，并能已知一方求另一方．‎ ‎ Ⅴ．课后作业 ‎ 习题3．10‎ ‎ Ⅵ．活动与探究 ‎ 如图，两个同心圆 被两条半径截得的弧AB 的长为6πcm，弧CD的 长为10πcm，又AC＝‎ ‎12 cm，求阴影部分ABDC的面积．‎ ‎ ‎ - 6 -‎ ‎ 分析：要求阴影部分的面积，需求扇形COD的面积与扇形AOB的面积之差．根据扇形面积S＝lR，l已知，则需要求两个半径OC与OA，因为OC＝OA+AC，AC已知，所以只要能求出OA即可．‎ ‎ 解：设OA＝R，OC＝R+12，∠O＝n°，根据已知条件有：‎ ‎6π=πR ①‎ ‎ 10π=π(R+12) ②‎ 由①/② 得. ‎ ‎∴3(R+12)=5R，∴R＝18．‎ ‎ ∴OC＝18+12＝30．‎ ‎ ∴S＝S扇形COD-S扇形AOB＝×10π× 30-×6π×18＝96πcm2．‎ ‎ 所以阴影部分的面积为96πcm2．‎ 板书设计 ‎§3．7 弧长及扇形的面积 ‎ 一、1. 复习圆的周长和面积计算公式；‎ ‎ 2．探索弧长的计算公式；‎ ‎ 3．例题讲解；‎ ‎ 4．想一想；‎ ‎ 5．弧长及扇形面积的关系；‎ ‎ 6．扇形面积的应用．‎ 二、课堂练习 三、课时小结 四、课后作业 备课资料 ‎ 一、参考例题 ‎[例]如图，已知正三角形ABC的边长为a，分别以A、B、C为圆心，以为半径的圆相切于点O1、O2、O3．求弧O1O2，弧O2O3，弧O3O1,围成的图形面积S(图中阴影部分)．‎ ‎ 分析：阴影部分的面积等于△ABC的面积减去三个扇形AO1O3、BO1O2、CO2O3‎ - 6 -‎ 的面积，而这三个扇形面积相等．‎ ‎ 解：∵S△ABC=a· a2，‎ ‎ S扇形AO1O3=a2，‎ ‎ ∴S阴影＝S△ABC-3S扇形AO1O3 =a2‎ - 6 -‎