【40套试卷合集】河南省郑州汝州区五校联考2019-2020学年数学九上期末模拟试卷含答案

【40套试卷合集】河南省郑州汝州区五校联考2019-2020学年数学九上期末模拟试卷含答案

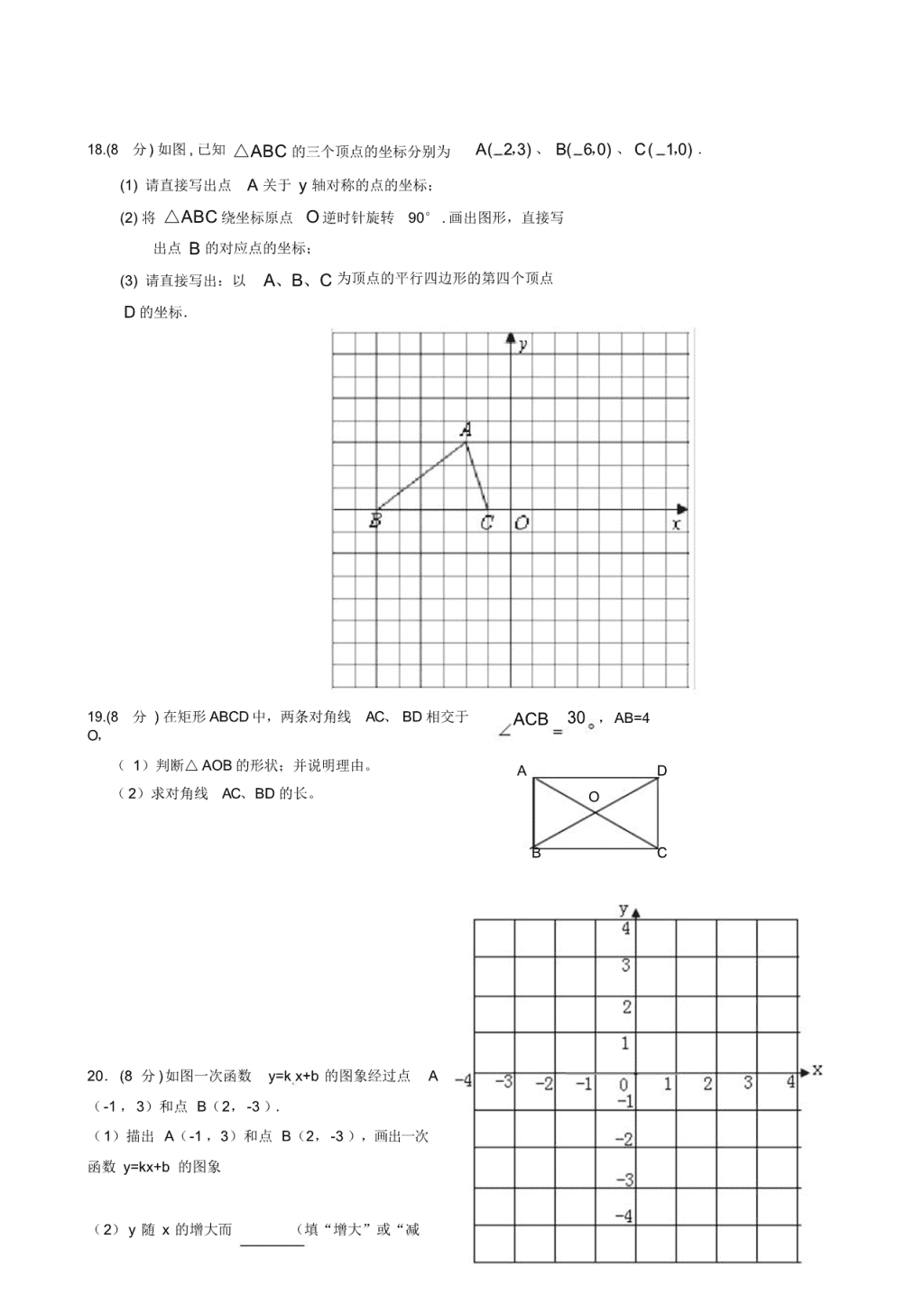
2019-2020 学年九上数学期末模拟试卷含答案 （考试时间 100 分钟满分 120 分） 亲爱的同学， 时间过得真快啊！转眼又一个学期了， 相信你在原有的基础上又掌握了许多新的数学知 识与 能力， 变得更加聪明了， 更加懂得应用数学来解决实际问题了。 现在让我们一起走进考场， 仔细思考， 认真作答，成功将属于你——数学学习的主人！ 一 、选择能手——看谁的命中率高（每小题只有一个正确的选项，将正确答案填在下面的表格内，每小题 3 分，共 24 分。） 题号 1 2 3 4 5 6 7 8 答案 1． 81 的平方 根是 A．3 B ．± 3 C ．-9 D ．± 9 2. 在下列长度的各组线段中，能组成直角三角形的是 A.5 ，6，7 B.5 ，12， 13 C.1 ，4， 9 D.5 ，11，12 3. 直角坐标系中 , 点 A(-3,4) 与点 B(-3,-4) 关于 A. 原点中心对称 B. y 轴轴对称 C. x 轴轴对称 D. 以上都不对 4．下列各点在函数 y=1－ 2x 的图象上的是 A．（2，－ 1） B. （ 0，2） C. （1， 0） D. （1，－ 1） 5. 下列命题正确的是 A. 正方形既是矩形，又是菱形 . B. 一组对边平行，另一组对边相等的四边形是等腰梯形 . C.一个多边形的内角相等，则它的边一定都相等 . D.矩形的对角线一定互相垂直 . 6. 下面四个数中与 11 最接近的数是 A D A ．2 B ．3 C ．4 D ．5 7. 如图，已知正方形 ABCD 的边长为 2，如果将线 段 BD 绕着点 B 旋转后，点 D 落在 CB 的延长线 D＇ B C 上的 D＇处，那么 A D＇为 A． 10 B. 2 2 C. 7 D. 2 3 8. 已知正比例函数 y=kx （ k≠0）的函数值 y 随 x 的增大而增大，则一次函数 y=x+k 的图象大致是 二、填空能手——看谁填得既快又准确 （每小题 3 分，共 24 分） 9. 7 的相反数是 ， 3 27 的倒数是 ， 25 的绝对值是 。 10. 边长为５ cm 的菱形，一条对角线长是 6cm，则 另一条对角线的长是 . 11. 若一个多边形的内角和等于 720 ，则这个多边形是 边形 . 12. 在函数 y=kx 的图像经过点（ 1， -2 ），则 k= ． 13. 已知 x+2y-2=0, 用含 x 的代数式表示 y= . 14. 已知，如图，平行四边形 ABCD 中， BE 平分 ∠ABC 交 AD 于 E，CF平分∠ BCD 交 BD 于 F，若 AB=3，BC=5， B 则 AE= ，EF= 。 A F E D C 14 题 15．如图，已知面积为 1 的正方形 ABCD 的对角线相交于点 O ，过点 O 任 A E D 作一条直线分别交 AD，BC 于 E，F ，则阴影部分的面积是 ． 16. 已知直线 y x 6 与 x 轴、 y 轴围成一个三角形，则这个三角形面积为 O ． 三、解答能手——看谁写得既全面又整洁（共 72分） 17．计算题（每小题 5 分，共 15 分） B F C 15 题 （1） 127 6 48 3 （2） 6 3 18 9 1 2 （3） 2 2 6 2 6 2 1 2 18.(8 分) 如图 , 已知 △ABC 的三个顶点的坐标分别为 A( 2，3) 、 B( 6，0) 、 C( 1，0) ． (1) 请直接写出点 A 关于 y 轴对称的点的坐标； (2) 将 △ABC 绕坐标原点 O 逆时针旋转 90° . 画出图形，直接写 出点 B 的对应点的坐标； (3) 请直接写出：以 A、B、C 为顶点的平行四边形的第四个顶点 D 的坐标． 19.(8 分 ) 在矩形 ABCD 中，两条对角线 AC、 BD 相交于 O， ACB 30 ，AB=4 （ 1）判断△ AOB 的形状；并说明理由。 A D （ 2）求对角线 AC、BD 的长。 O B C 20．(8 分 )如图一次函数 y=k x+b 的图象经过点 A （-1 ，3）和点 B（2， -3 ）． （1）描出 A（-1 ，3）和点 B（2，-3 ），画出一次 函数 y=kx+b 的图象 （2） y 随 x 的增大而 （填“增大”或“减 小”）. 21. (8 分) 如图，飞机在空中水平飞行，某一时刻刚好飞到一男孩子头顶上方 4000 米处，过了 20 秒， 飞机距离这个男孩头顶 5000 米. 飞机每小时飞行多少千米？ 22.(8 分) 甲、乙两人骑自行车分别从相距一定距离的 A、B 两地相向而行。假设他们都保持匀速行驶， 他们各自到 A 地的距离 s( 千米 )都是骑车时间 t( 时 )的函数，图象如图所示 . 根据图像解决下列问题： （1）出发时 在 A 地， A、B 两地相距 千米。（2 分） （2） v 甲 千米 / 时， v 乙 千米 / 时。（2分） （3）分别求出甲、乙在行驶过程中 s( 千米 ) 与 t( 时 )的函数关系式。 （4 分） 23． (9 分 ) 如图，平行四边形 ABCD 中， AB AC ， AB 1， BC 5 ．对角 线 AC，BD 相交于点 O ，将直线 AC 绕点 O 顺时针旋转，分别交 BC，AD 于点 E，F ． （1）当旋转角为 90 时，试说明四边形 ABEF 是平行四边形； （2）试说明在旋转过程中，线段 AF 与 EC 总保持相等； （3）在旋转过程中，四边形 BEDF 可能是菱形吗？如果不能，请说明理由； 如果能，说明理由并求出此时 AC 绕点 O 顺时针旋转的度数． F A D O B C E 24.(8 分) 暑假期间，小明和父母一起开车到距家 200 千米的景点旅游 . 出发前，汽车油箱内储油 45 升； 当行驶 150 千米时，发现油箱剩余 油量为 30 升 . (1) 已知油箱内余油量 y( 升) 是行驶路程 x( 千米 ) 的一次函数，求 y 与 x 的函数关系式； (2) 当油箱中余油量少于 3 升时， 汽车将自动报警 . 如果往返途中不加油， 他们能否在汽车报警前回到 家 ?请说明理由 . 八年数学 参考答案 （ 6 章） 2 4 A +4J 2 2019-2020 学年九上数学期末模拟试卷含答案 一、选择题（本题共 32 分，每小题 4 分） 下面各题均有四 个选项，其中只有一个 ．．是符合题意的． 1．抛物线 y (x 1)2 1的顶点坐标为 A． (1,1) B． (1, 1) C． ( 1,1) D． ( 1, 1) 2．若相交两圆的半径分别为 4 和 7，则它们的圆心距可能是 A．2 B．3 C． 6 D．11 3．在 Rt△ABC 中，∠ C＝90°，若 BC＝1，AB= 5 ，则 tanA 的值为 5 2 5 1 A． B． C． 5 5 2 D．2 4．如图，在⊙ O 中，直径 AB⊥弦 CD 于 E，连接 BD，若∠ D=30°， BD=2，则 AE 的长为 A．2 B．3 C．4 D．5 5．若正六边形的边长等于 4，则它的面积等于 A． 48 3 B． 24 3 C．12 3 D． 4 3 6．如图，以点 D 为位似中心，作△ ABC 的一个位似三 角形 A1B1C1，A，B，C 的对应点分别为 A1，B1， C1， DA1 与 DA的比值为 k，若两个三角形的顶点及点 D 均在如图所示的格点上，则 k 的值和点 C1 的坐标分 别为 A．2， (2,8) B．4， (2,8) C．2， (2,4) D．2， (4,4) 7．如图，抛物线 y ax bx c 与 x 轴交于点 ( 1,0) ，对称轴为 x 1，则下 列结论中正确的是 A． a B．当 C． c 0 x 1时， y 随 x 的增大而增大 0 D． x 3是一元二次方程 ax2 bx c 0的一个根 2 2 2 8．如图，在平面直角坐标系 xOy 中， A(2,0) ， B(0,2) ，⊙ C 的圆 心为点 C( 1,0) ，半径为 1．若 D 是⊙ C上的一个动点，线段 DA 与 y轴交于点 E，则 △ABE 面积的最大值是 8 A．2 B． 3 2 C． 2 2 2 D． 2 2 二、填空题（本题共 16 分，每小题 4 分） 9．如图，⊙ O 是△ABC 的外接圆，若∠ OCB＝40°，则∠ A= °． 10．将抛物线 y x 先向下平移 1 个单位长度后，再向右平移 1 个 单位长度，所得抛物线的解析式是 ． 11．如图，在 Rt△ABC 中，∠ ACB=90°，∠ B=30°，AB=4 ．以斜 边 AB 的中点 D 为旋转中心，把 △ ABC 按逆时针方向旋转 角 （ 0 120 ），当点 A 的对应点与点 C 重合时， B，C两 点 的对应点分别记为 E，F，EF 与 AB的交 点为 G，此时 等于 °，△ DEG 的面积为 ． 1 2 12．已知二次函数 y x x ，（ 1）它的最大值为 ；（2）若存在实数 m，n 使得当自变量 x 的取 2 值范围是 m≤ x≤n 时，函数值 y 的取值范围恰好是 3m≤y≤3n，则 m= ，n= ． 三、解答题（本题共 30 分，每小题 5 分） 13．计算： cos30 3 tan60 2sin 45 ． 14．已知关于 x 的方程 x 2x 2k 3 0 有两个不相等的实数根． （ 1）求 k 的取值范围； （ 2）若 k 为符合条件的最大整数，求此时方程的根． 15．已知抛物线 y x 4x 5 . （ 1）直接写出它与 x 轴、 y 轴的交点的坐标； （ 2）用配方法将 y x 4x 5 化 成 y a(x h) k 的形式． 16．已知：如图，在菱形 ABCD 中， E为 BC边上一点， ∠AED=∠B． （ 1）求证： △ABE∽△ DEA； （ 2）若 AB=4，求 AE DE 的值． 17．学校要围一个矩形花圃，花圃的一边利用足够长的墙，另三边 用总长为 36 米的篱笆恰好围成（如图所示） ．设矩形 的一边 AB 的长为 x 米（要求 AB＜ AD），矩形 ABCD的面 2 22 2 2 积为 S 平方米． （ 1）求 S与 x 之间的函数关系式，并直接写出自变量 x 的取值范围； （ 2）要想使花圃的面积最大， AB 边的长应为多少米？ 18．如图，在 Rt△ABC 中， C 90 ， AB 的垂直平分线与 BC，AB 的交点分别为 D，E． （1）若 AD=10， sin ADC 4 ，求 AC 的长和 tan B 的值； 5 （ 2）若 AD=1， ADC = ，参考（ 1）的计算过程直接写 出 t an 2 的值（用 s i n 和 c o s 的值表示）． 四、解答题（本题共 20 分，每小题 5 分） 19．如图所示，在平面直角坐标系 xOy 中，正方形 PABC 的边长为 1，将其沿 x 轴的正方向连续滚动，即 先以顶点 A 为旋转中心将正方形 PABC 顺时针旋转 90°得到第二个正方形，再以顶点 D 为旋转中心 将第二个正方形顺时针旋转 90°得到第三个正方形，依此方法继续滚动下去得到第四个正方形， ， 第 n个正方形．设滚动过程中的点 P 的坐标为 ( x, y) ． （ 1）画出第三个和第四个正方形的位置，并直接写出第三个正方形中的点 P 的坐标； （2）画出点 P(x, y) 运动的曲线（ 0≤ x ≤4），并直接写出该曲线与 x 轴所围成区域的面积． 20．已知函数 y x bx c（x ≥0），满足当 x =1 时， y 1 ， 且当 x = 0 与 x =4时的函数值相等． （ 1）求函数 y x2 bx c （x ≥0）的解析式并画出它的 图象（不要求列表） ； （ 2）若 f ( x) 表示自变量 x 相对应的函数值，且 f (x) x bx c (x 0), 又已知关于 x 的方程 2 ( x 0), f ( x) x k 有三个不相等的实数根，请利用图象直接写出实数 k 的取值范围． 21．已知：如图， AB 是⊙ O 的直径， AC 是弦，∠ BAC 的平分线与 ⊙O 的交点为 D，DE⊥AC，与 AC 的延长线交于点 E． （ 1）求证：直线 DE是⊙ O 的切线； （ 2）若 OE与 AD 交于点 F， cos BAC 4 DF，求 的值． 5 AF 2 22．阅读下列材料： 题目：已知实数 a， x 满足 a＞ 2 且 x＞2，试判断 ax与 a x 的大小关系，并加以说明 . 思路：可用 “ 求差法 ”比较两个数的大小，先列出 ax 与 a x 的差 y ax (a x) ，再 说明 y 的符号即可 现给出如下利用函数解 决问题的方法： 简解：可将 y 的代数式整理成 y (a 1)x a ，要判断 y 的符号可借助函数 y (a 1)x a 的图象和性质 解决 . 参考以上解题思路解决以下问题： 已知 a，b，c 都是非负数， a＜5，且 a2 a 2b 2c 0 ， a 2b 2c 3 0 ． （1）分别用含 a 的代数式表示 4b，4c； （2）说明 a，b，c 之间的大小关系． 五、解答题（本题共 22 分，第 23 题 7 分，第 24 题 7 分，第 25 题 8 分） 23．已知抛物线 y kx (k 2)x 2 （其中 k 0 ）． （ 1）求该抛物线与 x 轴的交点坐标及顶点坐标 (可以用含 k 的代数式表示 )； （ 2）若记该抛物线的顶点坐标为 P(m,n) ，直接写出 n 的最小值； （ 3）将该抛物线先向右平移 1 个单位长度，再向上平移 2 1 个单位长度，随着 k 的变化，平移后的抛 k 物线的顶点都在某个新函数的图象上，求这个新函数的解析式（不要求写自变量的取值范围） ． 24．已知：如图，正方形 ABCD 的边长为 a，BM， DN 分别平分正方形的两个外角，且满足 MAN 45 ，连结 MC，NC，MN ． （1）填空：与 △ABM 相似的三角形是 △ ， B M D N= ；（用含 a 的代数式表示） （2）求 MCN 的度数； （3）猜想线段 BM，DN 和 MN 之间的等量关系并 证明你的结论．