江西专版2020中考数学复习方案第七单元图形的变化第29课时视图投影与尺规作图课件

江西专版2020中考数学复习方案第七单元图形的变化第29课时视图投影与尺规作图课件

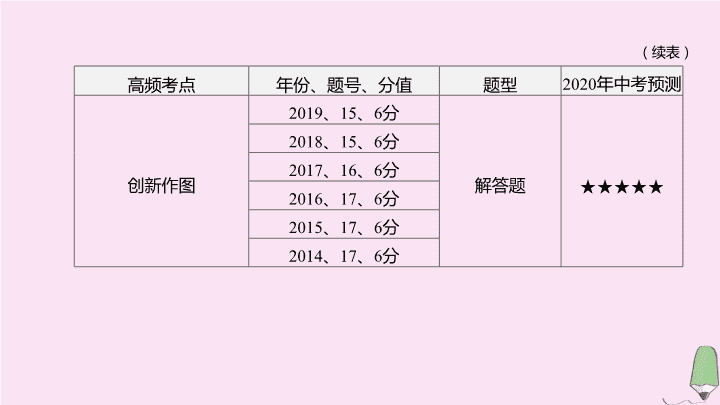
第 29 课时 视图、投影与尺规作图 第七单元　图形的变化 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 几何体与三视图 2019 、 3 、 3 分 选择题 ★★★★★ 2018 、 3 、 3 分 2016 、 4 、 3 分 2015 、 3 、 3 分 几何体与展开图 2014 、 5 、 3 分 选择题 ★ （续表） 高频考点 年份、题号、分值 题型 2020 年中考预测 创新作图 2019 、 15 、 6 分 解答题 ★★★★★ 2018 、 15 、 6 分 2017 、 16 、 6 分 2016 、 17 、 6 分 2015 、 17 、 6 分 2014 、 17 、 6 分 考点一　三视图 考点聚焦 1. 三视图的概念及画法 三 视 图 主视图 　 正投影情况下 , 在正面内得到的 ① 　　 　 观察 物体的视图   左视图 　 正投影情况下 , 在侧面内得到的 ② 　　　 观察 物体的视图   俯视图 　 正投影情况下 , 在水平面内得到的 ③ 　　　 观察 物体的视图   从前向后 从左到右 从上到下 ( 续表 ) 画 法 主视图 和俯视图要 ④ 　　　 ,   主视图和左视图要 ⑤ 　　　 ,   左视图和俯视图要 ⑥ 　　　　 ,   看得见的轮廓线通常画成 ⑦ 　　　　 ,  看不见的轮廓线通常画成 ⑧ 　 　　   长对正 高平齐 宽相等 实线 虚线 2. 常见几何体的三视图 几 何 体 三 视 图 考点二　投影 平行投影 　 由 ⑨ 　　　　 光线形成的投影叫做平行投影 ; 物体在太阳光照射下可以看成平行投影 ; 投影线 ⑩ 　　　　 于投影面产生的投影叫做正投影   中心投影 　 由同一点 ( 点光源 ) 发出的光线形成的投影叫做中心投影 , 如灯光下某物体的投影 平行 垂直 常见几何体 展开图 图示 六个全等的正方形 两个同等大小的圆和一个 ⑪ 　　　   矩形 1. 常见几何体的展开图 考点三　立体图形的展开与折叠 ( 续表 ) 常见几何体 展开图 图示 一个圆和一个 ⑫ 　　　   两个全等的三角形和三个矩形 扇形 2. 正方体表面展开图类型 ( 相同颜色表示相对的面 ) 一四一型 二三一型 二二二 型 三三型 【 温馨提示 】 (1) 正方体表面展开图中不能出现 图形 ; (2) 若出现 类型 , 另外两面必定在两侧 , 可借助此特点来排除错误选项 . 考点四　尺规作图 1 . 作 一条 线段 等于已知线段 步骤 :(1) 作射线 OP ; (2) 在 OP 上截取 OA=a , OA 即为所求线段 　　 以下几种是初中涉及的基本尺规作图 , 限定作图工具只有圆规和无刻度的直尺 . ( 续表 ) 2 . 作 一个 角 等于已知 角 步骤 :(1) 在 ∠ α 上以点 O 为圆心 , 以适当的长为半径作弧 , 交 ∠ α 的两边于点 P , Q ; (2) 作射线 O'A ; (3) 以点 O' 为圆心 , OP 长为半径作弧 , 交 O'A 于点 M ; (4) 以点 M 为圆心 , PQ 长为半径作弧 , 交前弧于点 N ; (5) 过点 N 作射线 O'B , ∠ BO'A 即为所求角 ( 续表 ) ( 续表 ) ( 续表 ) 题组一　必会题 对点演练 1 . [2019· 淮安 ] 如图 29-1 是由 4 个相同的小正方体搭成的几何体 , 则该几何体的主视图是 ( 　　 ) 图 29-1 图 29- 2 C 2 . [2019· 益阳 ] 下列几何体 , 其侧面展开图为扇形的是 ( 　　 ) 图 29-3 C 3 . 小明拿一个等边三角形木框在太阳下玩耍 , 发现等边三角形木框在地面上的投影不可能是 ( 　　 ) 图 29-4 [ 答案 ] B 　 [ 解析 ] 当等边三角形木框与阳光平行时 , 投影是 A; 当等边三角形木框与阳光有一定角度时 , 投影是 C 或 D; 投影不可能是 B . 故选 B . 4 . [2019· 遂宁 ] 如图 29-5 为正方体的一种平面展开图 , 各面都标有数字 , 则数字 -2 的面与其对面上的数字之积是 ( 　　 ) A . -12 B . 0 C . -8 D . -10 图 29-5 [ 答案 ] A 　 [ 解析 ] 正方体折叠还原后 -2 的对面是 6, 所以 -2×6 = -12 . 图 29-6 D 题组二　易错题 【 失分点 】 混淆物体轮廓线的表示方法造成错误 ; 画三视图时忽视全透明物体本身的透明特性引起错误 ; 平行投影与中心投影易混淆 . 6 . [2019· 宁波 ] 如图 29-7, 下列关于物体的主视图画法正确的是 ( 　　 ) 图 29-7 图 29-8 C 7 . 如图 29-9, 此时树的影子是在 　　　　 ( 填 “ 太阳光 ” 或 “ 灯光 ”) 下的影子 .  图 29-9 [ 答案 ] 太阳光 　 [ 解析 ] 通过作图发现相应的直线是平行关系 . 考向一　三视图 例 1 [2019· 滨州 ] 如图 29-10, 一个几何体由 5 个大小相同、棱长为 1 的小正方体搭成 , 下列说法正确的是 ( 　　 ) A . 主视图的面积为 4 B . 左视图的面积为 4 C . 俯视图的面积为 3 D . 三种视图的面积都是 4 图 29-10 [ 答案 ] A 　 [ 解析 ] 观察该几何体 , 主视图有四个小正方形 , 面积为 4; 左视图有 3 个小正方形 , 面积为 3; 俯视图有四个小正方形 , 面积为 4, 故 A 正确 . | 考向精练 | 1 . [2019· 江西 3 题 ] 如图 29-11 是手提水果篮抽象的几何体 , 以箭头所指的方向为主视图方向 , 则它的俯视图为 ( 　　 ) 图 29-12 图 29-11 A 2 . [2015· 江西 3 题 ] 如图 29-13 的几何体的左视图为 ( 　　 ) 图 29-13 D 图 29-14 3 . [2018· 江西 3 题 ] 如图 29-15 的几何体的左视图为 ( 　　 ) 图 29-15 D 图 29-16 4 . [2016· 江西 4 题 ] 有两个完全相同的长方体 , 按如图 29-17 方式摆放 , 其主视图是 ( 　　 ) 图 29-17 C 图 29-1 8 5 . [2017· 江西 10 题 ] 如图 29-19, 正三棱柱的底面周长为 9, 截去一个底面周长为 3 的正三棱柱 , 所得几何体的俯视图的周长是 　　　　 .  图 29-19 [ 答案 ] 8 　 [ 解析 ] 根据题意可知 , 正三棱柱的俯视图为正三角形 . ∵底面周长为 9, ∴边长为 3 . ∵截去一个底面周长为 3 的正三棱柱 , 即俯视图也为正三角形 , ∴截去的正三棱柱底面正三角形的边长为 1 . 如图 , 虚线为切割线 , ∴所得几何体的俯视图的周长为 8 . 考向二　立体图形的展开与折叠 图 29-20 例 2 由如图 29-20 所示的正方体的平面展开图可知 , 原正方体 “ 中 ” 字所在面的对面的汉字是 ( 　　 ) A . 国 B . 的 C . 中 D . 梦 B | 考向精练 | 图 29-22 [2014· 江西 5 题 ] 如图 29-21, 贤贤同学用手工纸制作了一个台灯灯罩 , 做好后发现上口太小了 , 于是他把纸灯罩对齐压扁 , 剪去上面一截后 , 正好合适 . 以下裁剪示意图中 , 正确的是 ( 　　 ) A 图 29-21 考向三　创新作图 图 29-23 例 3 [2019· 赣州模拟 ] 如图 29-23, 四边形 ABCD 是菱形 , BE 是 AD 边上的高 , 请仅用无刻度的直尺作图 ( 保留作图痕迹 ) . (1) 在图①中 , BD=AB , 作 △ BCD 的边 BC 上的中线 DF ; (2) 在图②中 , BD ≠ AB , 作 △ ABD 的边 AB 上的高 DF. 解 :(1) 如图① , DF 即为所求 . 图 29-23 例 3 [2019· 赣州模拟 ] 如图 29-23, 四边形 ABCD 是菱形 , BE 是 AD 边上的高 , 请仅用无刻度的直尺作图 ( 保留作图痕迹 ) . (2) 在图②中 , BD ≠ AB , 作 △ ABD 的边 AB 上的高 DF. (2) 如图② , DF 即为所求 . | 考向精练 | 1 . [2018· 江西 15 题 ] 如图 29-24, 在四边形 ABCD 中 , AB ∥ CD , AB= 2 CD , E 为 AB 的中点 . 请仅用无刻度的直尺分别按下列要求画图 ( 保留画图痕迹 ) . (1) 在图①中 , 画出 △ ABD 的 BD 边上的中线 ; (2) 在图②中 , 若 BA=BD , 画出 △ ABD 的 AD 边上的高 . 图 29-24 解 :(1) 如图① , AF 为所求 . 1 . [2018· 江西 15 题 ] 如图 29-24, 在四边形 ABCD 中 , AB ∥ CD , AB= 2 CD , E 为 AB 的中点 . 请仅用无刻度的直尺分别按下列要求画图 ( 保留画图痕迹 ) . (2) 在图②中 , 若 BA=BD , 画出 △ ABD 的 AD 边上的高 . 图 29-24 (2) 如图② , BH 为所求 . 2 . [2019· 江西样卷四 ] 如图 29-25, 已知正方形 ABCD 和 △ ADE , AE=ED , 请仅用无刻度的直尺按要求画图 . (1) 在图①中 , 找出 AD 的中点 F ; (2) 在图②中 , 画出 AD 的一个三等分点 G. 图 29-25 解 :(1) 如图① , 点 F 即为所求 . (2) 如图② , 点 G 即为所求 . 图 29-26 解 :(1) 如图①所示 , 四边形 ACEF 即为所求 : 图 29-26 (2) 如图②所示 ,△ DEF 即为所求 .