鄂尔多斯专版2020中考数学复习方案第七单元图形的变化第29课时平移与旋转课件

鄂尔多斯专版2020中考数学复习方案第七单元图形的变化第29课时平移与旋转课件

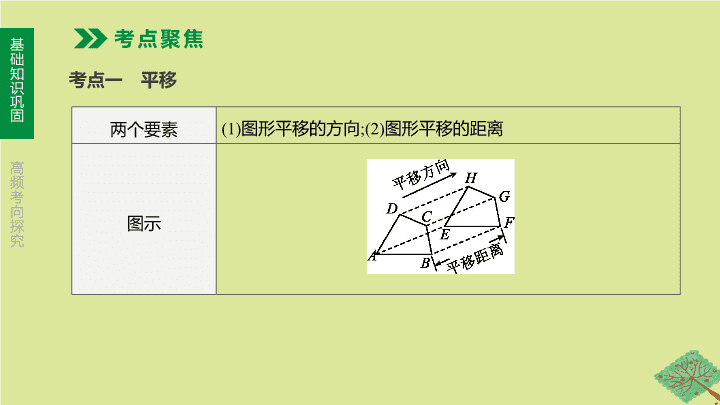
第 29 课时 平移与旋转 第七单元　图形的变化 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 图形的平移 ★★ 图形的旋转 10 题 ,3 分 9 题 ,3 分 5 题 ,3 分 24 题 ,3 分 23 题 ,11 分 ★★★★ 考点一　平移 考点聚焦 两个要素 (1) 图形平移的方向 ;(2) 图形平移的距离 图示 ( 续表 ) 性质 (1) 平移前后对应线段平行 ( 或共线 ) 且 ① 　　　 , 对应点所连的线段 ② 　　　 　 ;  (2) 对应角分别 ③ 　　　　 , 且对应角的两边分别平行、方向一致 ;  (3) 平移变换后的图形与原图形 ④ 　 　   网格作图 的步骤 　 (1) 确定平移方向和平移距离 ;(2) 找原图形关键点 ;(3) 按平移方向和距离平移各关键点 ;(4) 按原图形顺次连接各关键点平移后的对应点 , 得到平移后的图形 相等 平行 ( 或共线 ) 且相等 相等 全等 考点二　旋转 三个要素 (1) 旋转中心 ;(2) 旋转方向 ;(3) 旋转角度 图示 ( 续表 ) 性质 (1) 对应点到旋转中心的距离 ⑤ 　　　 ;  (2) 对应点与旋转中心所连线段的夹角等于 ⑥ 　　　　 ;  (3) 旋转前后的图形 ⑦ 　　　   网格作图 的步骤 (1) 确定旋转中心、旋转方向及旋转角 ;(2) 找原图形的关键点 ;(3) 连接关键点与旋转中心 , 按旋转方向与旋转角将它们旋转 , 得到各关键点的对应点 ;(4) 按原图形依次连接各关键点的对应点 , 得到旋转后的图形 相等 旋转角 全等 【 温馨提示 】 旋转对称与中心对称的关系 : 中心对称是旋转角为 180 ° 的旋转对称 . 题组一　必会题 对点演练 1 . 如图 29-1, 将 △ ABC 沿着由点 B 到点 C 的方向平移到 △ DEF , 如果 BC =5, EC =3, 那么平移的距离为 ( 　　 ) A . 2 B . 3 C . 5 D . 7 A 图 29-1 2 . 如图 29-2, 将一个含 30° 角的直角三角板 ABC 绕点 A 旋转 , 得到直角三角板 AB'C' , 且点 B , A , C' 在同一条直线上 , 则三角板 ABC 旋转的角度是 ( 　　 ) A . 60° B . 90° C . 120° D . 150° [ 答案 ] D 　 [ 解析 ] 旋转角是∠ CAC' = 180°-30°=150° . 故选 D . 图 29-2 3 . 如图 29-3, 将线段 AB 绕点 O 顺时针旋转 90° 得到线段 A'B' , 那么 B (-2,5) 的对应点 B' 的坐标是 ( 　　 ) A . (2,5) B . (5,2) C . (2,-5) D . (5,-2) 图 29-3 B 图 29-4 [ 答案 ] 1 【 失分点 】 在旋转或平移的过程中对相关要素把握不准确 , 构图错误 ; 在图形变换过程中 , 忽视分类讨论 . 题组二　易错题 5 . [2018· 济宁 ] 如图 29-5, 在平面直角坐标系中 , 点 A , C 在 x 轴上 , 点 C 的坐标为 (-1,0), AC =2 . 将 Rt△ ABC 先绕点 C 顺时针旋转 90°, 再向右平移 3 个单位长度 , 则变换后点 A 的对应点的坐标是 ( 　　 ) A . (2,2) B . (1,2) C . (-1,2) D . (2,-1) 图 29-5 [ 答案 ] A 　 [ 解析 ] 如图 , 根据题意作出各变换过程后的图形 . ∵点 C 的坐标为 (-1,0), AC =2, ∴将 Rt△ ABC 绕点 C 顺时针旋转 90° 后 , 点 A' 的坐标为 (-1,2), 再向右平移 3 个单位长度 , 则变换后点 A″ 的坐标为 (2,2) . 故选 A . 6 . 在 Rt△ ABC 中 , ∠ C =90°, BC =3, AC =4, 将 △ ABC 绕点 C 旋转 , 旋转后的三角形记为 △ A 1 B 1 C , 直线 A 1 B 1 与直线 AC 交于点 D , 当 B 1 C ⊥ AB 时 , 线段 AD 的值为 　　　　 .  考向一　图形的平移 图 29-6 例 1 如图 29-6, 将 △ ABE 向右平移 2 cm 得到 △ DCF , 如果 △ ABE 的周长是 16 cm, 那么四边形 ABFD 的周长是 ( 　　 ) A . 16 cm B . 18 cm C . 20 cm D . 21 cm [ 答案 ] C 　 [ 解析 ] ∵将 △ ABE 向右平移 2 cm 得到 △ DCF , ∴ EF = AD =2 cm, AE = DF. ∵ △ ABE 的周长为 16 cm, ∴ AB + BE + AE =16 cm, ∴四边形 ABFD 的周长 = AB + BE + EF + DF + AD = AB + BE + AE + EF + AD =16+2+2=20(cm) . 故选 C . 【 方法点析 】 (1) 对应点间的距离等于平移的距离 ;(2) 利用 “ 平移前后的两个图形全等 ”“ 平移前后对应线段平行 ( 或共线 ) 且相等 ” 是解决平移问题的基本方法 . | 考向精练 | 图 29-7 [ 答案 ] B 考向二　图形的旋转 图 29-8 例 2 [2019· 荆州 ] 如图 29-8 ① , 等腰直角三角形 OEF 的直角顶点 O 为正方形 ABCD 的中心 , 点 C , D 分别在 OE 和 OF 上 , 现将 △ OEF 绕点 O 逆时针旋转角 α (0° <α< 90°), 连接 AF , DE ( 如图 29-8 ② ) . (1) 在图②中 , ∠ AOF = 　　　　 ; ( 用含 α 的式子表示 )  (2) 在图②中 , 猜想 AF 与 DE 的数 量关系 , 并证明你的结论 . ① ② 解 :(1)90°- α 　 [ 解析 ] ∵ △ OEF 绕点 O 逆时针旋转角 α , ∴∠ DOF = ∠ COE = α , ∵四边形 ABCD 为正方形 , ∴∠ AOD =90°, ∴∠ AOF =90°- α. 故答案为 90°- α. 图 29-8 例 2 [2019· 荆州 ] 如图 29-8 ① , 等腰直角三角形 OEF 的直角顶点 O 为正方形 ABCD 的中心 , 点 C , D 分别在 OE 和 OF 上 , 现将 △ OEF 绕点 O 逆时针旋转角 α (0° <α< 90°), 连接 AF , DE ( 如图 29-8 ② ) . (2) 在图②中 , 猜想 AF 与 DE 的数量关系 , 并证明你的结论 . ① ② 解 : (2) AF = DE. | 考向精练 | 图 29-9 1 . [2017· 鄂尔多斯 5 题 ] 如图 29-9 是由一副三角尺 ABC 与 DEF 拼成的图案 , 若将三角尺 DEF 绕点 M 按顺时针方向旋转 , 则边 DE 与边 AB 第一次平行时 , 旋转角的度数是 ( 　　 ) A . 75° B . 60° C . 45° D . 30° [ 答案 ] C 　 [ 解析 ] 如图 , 过点 M 作 MH ∥ AB 交 BC 于点 H. ∵ AB ⊥ BC , ∴ MH ⊥ BC , ∴ △ BMH 是等腰直角三角形 , ∴∠ BMH =45°, ∴若将三角尺 DEF 绕点 M 按顺时针方向旋转 , 边 DE 与边 AB 第一次平行时 , 旋转角的度数是 45° . 故选 C . 图 29-10 2 . [2014· 鄂尔多斯 4 题 ] 如图 29-10, 在 △ ABC 中 , ∠ B =50°, 在同一平面内 , 将 △ ABC 绕点 A 按逆时针方向旋转到 △ AB‘C’ 的位置 , 使 AB‘ ⊥ BC , 连接 CC’ , 则∠ AC‘C = 　 　 度 .  [ 答案 ] 70 考向三　平移和旋转作图 例 3 [2019· 淮安 ] 如图 29-11, 方格纸上每个小正方形的边长均为 1 个单位长度 , 点 A , B 都在格点上 ( 两条网格线的交点叫格点 ) . (1) 将线段 AB 向上平移两个单位长度 , 点 A 的对应点为点 A 1 , 点 B 的对应点为点 B 1 , 请画出平移后的线段 A 1 B 1 ; (2) 将线段 A 1 B 1 绕点 A 1 按逆时针方向旋转 90°, 点 B 1 的对应点为点 B 2 , 请画出旋转后的线段 A 1 B 2 ; (3) 连接 AB 2 , BB 2 , 求 △ ABB 2 的面积 . 图 29-11 解 :(1) 如图 , 线段 A 1 B 1 即为所求 . 例 3 [2019· 淮安 ] 如图 29-11, 方格纸上每个小正方形的边长均为 1 个单位长度 , 点 A , B 都在格点上 ( 两条网格线的交点叫格点 ) . (2) 将线段 A 1 B 1 绕点 A 1 按逆时针方向旋转 90°, 点 B 1 的对应点为点 B 2 , 请画出旋转后的线段 A 1 B 2 ; 图 29-11 解 : (2) 如图 , 线段 A 1 B 2 即为所求 . 例 3 [2019· 淮安 ] 如图 29-11, 方格纸上每个小正方形的边长均为 1 个单位长度 , 点 A , B 都在格点上 ( 两条网格线的交点叫格点 ) . (3) 连接 AB 2 , BB 2 , 求 △ ABB 2 的面积 . 图 29-11 【 方法点析 】 求一个图形旋转、平移后的图形的某点的坐标 , 一般应把握三点 : 一是图形平移、旋转的性质 ; 二是图形的全等关系 ; 三是点所在的象限 . | 考向精练 | 图 29-12 [2018· 阜新 ] 如图 29-12,△ ABC 在平面直角坐标系内 , 顶点的坐标分别为 A (-4,4), B (-2,5), C (-2,1) . (1) 平移 △ ABC , 使点 C 移到点 C 1 (-2,-4), 画出平移后的 △ A 1 B 1 C 1 , 并写出点 A 1 , B 1 的坐标 ; (2) 将 △ ABC 绕点 (0,3) 旋转 180°, 得到 △ A 2 B 2 C 2 , 画出旋转后的 △ A 2 B 2 C 2 ; (3) 求 (2) 中的点 C 旋转到点 C 2 的过程中 , 点 C 经 过的路径长 ( 结果保留 π) . 解 :(1) 如图 ,△ A 1 B 1 C 1 为所求作的三角形 , ∴ A 1 (-4,-1), B 1 (-2,0) . 图 29-12 [2018· 阜新 ] 如图 29-12,△ ABC 在平面直角坐标系内 , 顶点的坐标分别为 A (-4,4), B (-2,5), C (-2,1) . (2) 将 △ ABC 绕点 (0,3) 旋转 180°, 得到 △ A 2 B 2 C 2 , 画出旋转后的 △ A 2 B 2 C 2 ; 解 :(2) 如图 ,△ A 2 B 2 C 2 为所求作的三角形 . 图 29-12 [2018· 阜新 ] 如图 29-12,△ ABC 在平面直角坐标系内 , 顶点的坐标分别为 A (-4,4), B (-2,5), C (-2,1) . (3) 求 (2) 中的点 C 旋转到点 C 2 的过程中 , 点 C 经过的路径长 ( 结果保留 π) . 考向四　平移、旋转与其他知识的综合运用 例 3 [2019· 日照 ] 如图 29-13, 在矩形 ABCD 中 , 对角线 AC 的中点为 O , 点 G , H 在对角线 AC 上 , AG = CH , 直线 GH 绕点 O 逆时针旋转 α 角 , 与边 AB , CD 分别相交于点 E , F ( 点 E 不与点 A , B 重合 ) . (1) 求证 : 四边形 EHFG 是平行四边形 ; (2) 若∠ α =90°, AB =9, AD =3, 求 AE 的长 . 图 29-13 解 :(1) 证明 : ∵对角线 AC 的中点为 O , ∴ AO = CO , 又∵ AG = CH , ∴ GO = HO , ∵四边形 ABCD 是矩形 , ∴ AD = BC , CD = AB , CD ∥ AB , ∴∠ DCA = ∠ CAB , 又∵ CO = AO , ∠ FOC = ∠ EOA , ∴ △ COF ≌△ AOE (ASA), ∴ FO = EO , 又∵ GO = HO , ∴四边形 EHFG 是平行四边形 . 例 3 [2019· 日照 ] 如图 29-13, 在矩形 ABCD 中 , 对角线 AC 的中点为 O , 点 G , H 在对角线 AC 上 , AG = CH , 直线 GH 绕点 O 逆时针旋转 α 角 , 与边 AB , CD 分别相交于点 E , F ( 点 E 不与点 A , B 重合 ) . (2) 若∠ α =90°, AB =9, AD =3, 求 AE 的长 . 图 29-13 解 :(2) 如图 , 连接 CE , ∵∠ α =90°, ∴ EF ⊥ AC , 且 AO = CO , ∴ EF 是 AC 的垂直平分线 , ∴ AE = CE , 在 Rt△ BCE 中 , CE 2 = BC 2 + BE 2 , ∴ AE 2 =(9- AE ) 2 +9, ∴ AE =5 . | 考向精练 | 图 29-14 [2018· 临沂 ] 将矩形 ABCD 绕点 A 顺时针旋转 α (0° <α< 360°), 得到矩形 AEFG. (1) 如图 29-14, 当点 E 在 BD 上时 , 求证 : FD = CD. (2) 当 α 为何值时 , GC = GB ? 画出图形 , 并说明理由 . 解 :(1) 证明 : 如图① , 连接 AF. 由四边形 ABCD 是矩形 , 结合旋转可得 BD = AF , ∠ EAF = ∠ ABD. ∵ AB = AE , ∴∠ ABD = ∠ AEB , ∴∠ EAF = ∠ AEB , ∴ BD ∥ AF , ∴四边形 BDFA 是平行四边形 , ∴ FD = AB. ∵ AB = CD , ∴ FD = CD. ① 图 29-14 [2018· 临沂 ] 将矩形 ABCD 绕点 A 顺时针旋转 α (0° <α< 360°), 得到矩形 AEFG. (2) 当 α 为何值时 , GC = GB ? 画出图形 , 并说明理由 . 解 :(2) 当 α =60° 或 α =300° 时 , GC = GB. 理由 : 如图② , 当点 G 位于 BC 的垂直平分线上 , 且在 BC 的右边时 , 易知点 G 也是 AD 的垂直平分线上的点 , 则 DG = AG. 又∵ AG = AD , ∴ △ ADG 是等边三角形 , ∴∠ DAG =60°, ∴ α =60° . 如图③ , 当点 G 位于 BC 的垂直平分线上 , 且在 BC 的左边时 , 同理可知 ,△ ADG 是等边三角形 , ∴∠ DAG =60° . 此时 α =300° . 综上所述 , 当 α 为 60° 或 300° 时 , GC = GB. ② ③