- 2021-11-10 发布 |
- 37.5 KB |
- 12页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012年黑龙江省牡丹江市中考数学试题(含答案)
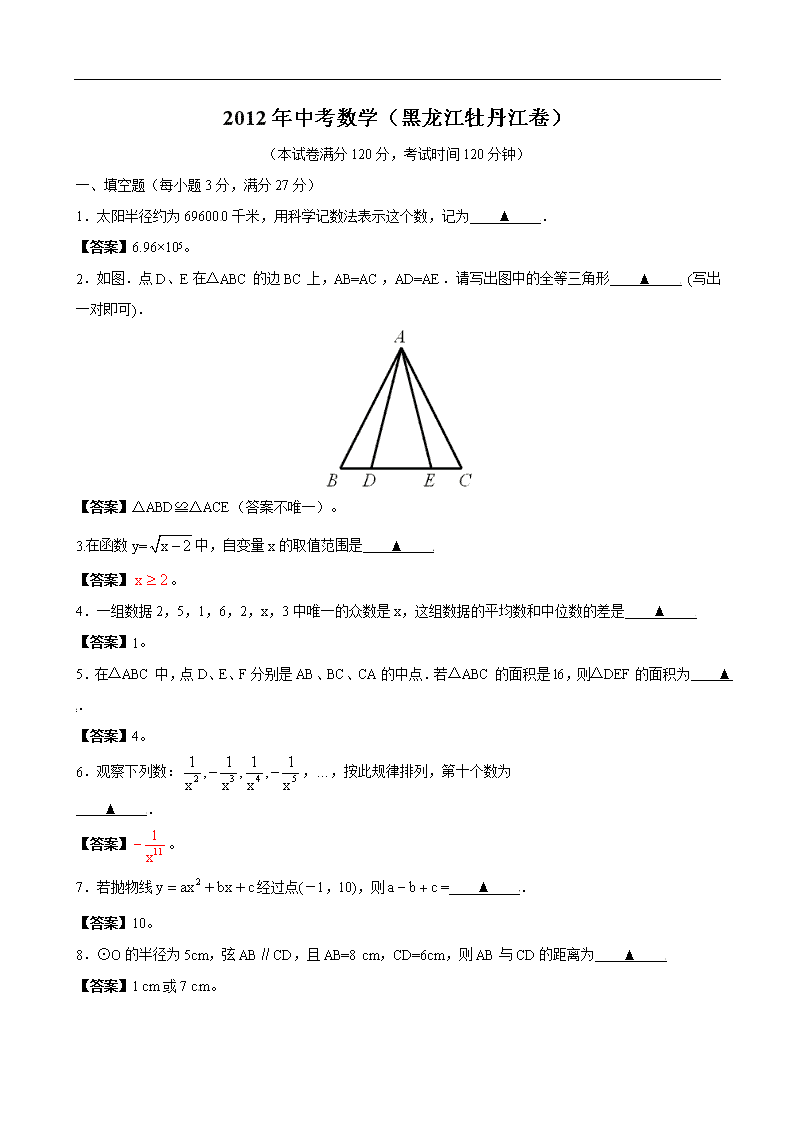
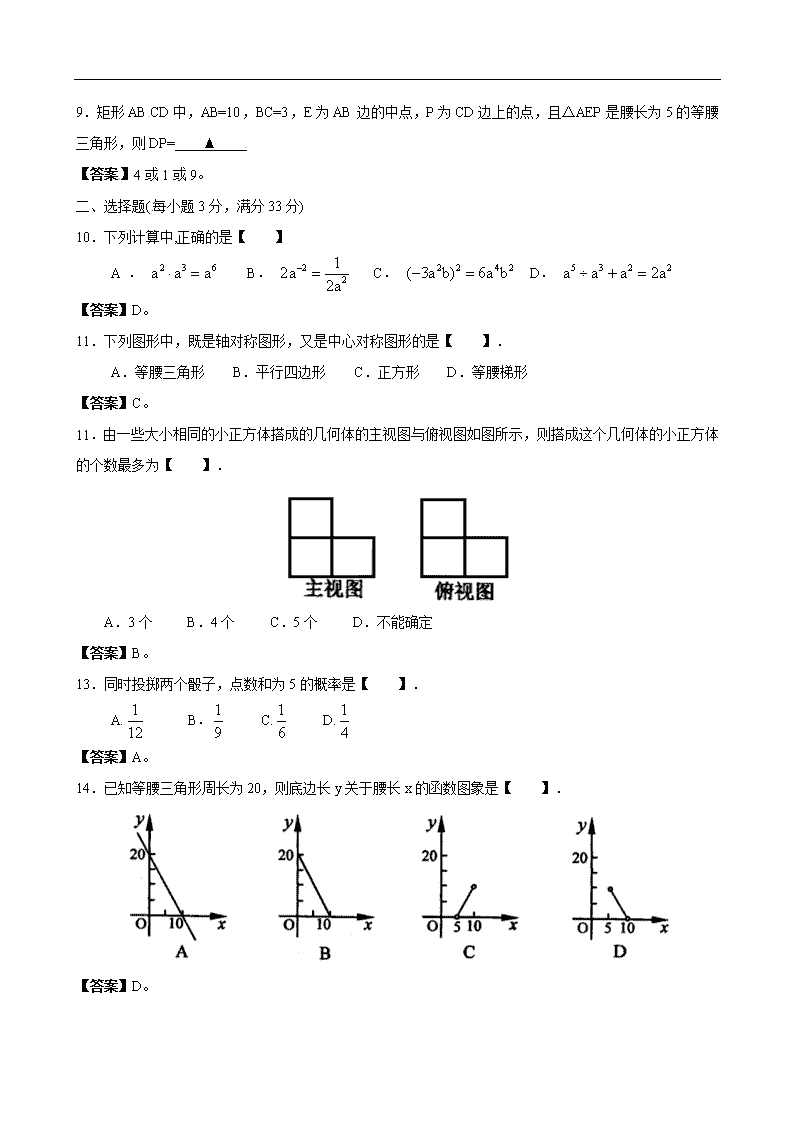
2012年中考数学(黑龙江牡丹江卷) (本试卷满分120分,考试时间120分钟) 一、填空题(每小题3分,满分27分) 1.太阳半径约为696000千米,用科学记数法表示这个数,记为 ▲ . 【答案】6.96×105。 2.如图.点D、E在△ABC的边BC上,AB=AC,AD=AE.请写出图中的全等三角形 ▲ (写出一对即可). 【答案】△ABD≌△ACE(答案不唯一)。 3.在函数y=中,自变量x的取值范围是 ▲ 【答案】。 4.一组数据2,5,1,6,2,x,3中唯一的众数是x,这组数据的平均数和中位数的差是 ▲ 【答案】1。 5.在△ABC中,点D、E、F分别是AB、BC、CA的中点.若△ABC的面积是l6,则△DEF的面积为 ▲ . 【答案】4。 6.观察下列数:,…,按此规律排列,第十个数为[来源:学|科|网Z|X|X|K] ▲ . 【答案】。 7.若抛物线经过点(-1,10),则= ▲ . 【答案】10。 8.⊙O的半径为5cm,弦AB∥CD,且AB=8 cm,CD=6cm,则AB与CD的距离为 ▲ 【答案】1 cm或7 cm。 9.矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP= ▲ 【答案】4或1或9。 二、选择题(每小题3分,满分33分) 10.下列计算中,正确的是【 】 A . B. C. D. 【答案】D。 11.下列图形中,既是轴对称图形,又是中心对称图形的是【 】. A.等腰三角形 B.平行四边形 C.正方形 D.等腰梯形 【答案】C。 11.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示,则搭成这个几何体的小正方体的个数最多为【 】. A.3个 B.4个 C.5个 D.不能确定 【答案】B。 13.同时投掷两个骰子,点数和为5的概率是【 】. A. B. C. D. 【答案】A。 14.已知等腰三角形周长为20,则底边长y关于腰长x的函数图象是【 】. 【答案】D。 15.如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有【 】. A.4对 B.5对 C.6对 D.7对 【答案】B。 16.抛物线与x轴的交点坐标是(-l,0)和(3,0),则这条抛物线的对称轴是【 】. A.直线x=-1 8.直线x=0 C.直线x=1 D.直线x= 3 【答案】C。 17.菜种商品每件的标价是330元,按标价的八折销售时,仍可获利l0%,则这种商品每件的进价为【 】, A.240元 B.250元 C.280元 D.300元 【答案】A。 18.如图,A(,1),B(1,).将△AOB绕点O旋转l500得到△A′OB′,,则此时点A的对应点A′的坐标为【 】. A.(-,-l) B.(-2,0) C.(-l,-)或(-2,0) D.(-,-1)或(-2,0) 【答案】C。 19.在甲乙两班进行的定点投篮中,每班选八名选手,每人投篮l0次.甲乙两班的比赛成绩(投中次数)统计如下表:甲乙两班投中次数的平均数都是5,且S2甲=1.5 甲 3 4 4 5 5 6 6 7 乙 3 3 4 5 6 6 6 7 请你通过计算,选择正确的答案为【 】 A.S乙2=1.4,甲班成绩比乙班更稳定 B.S乙2=2,甲班成绩比乙班更稳定 C.S乙2=1.5,甲乙两班成绩一样稳定 D.不能确定甲乙两班成绩哪一个更稳定 【答案】B。 20.如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点, 且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=1200,③AH+CH=DH,④AD 2=OD·DH中,正确的是【 】. A. ①②④ B. ①②③ C. ②③④ D. ①②③④ 【答案】D。 三、解答题(满分60分) 21.先化简,再求值.其中,-3<b<且b为整数 【答案】解:原式=。 ∵,-3<b<且b为整数,∴b=-2或0。 ∴当,b=-2时,原式=1-(-2)=3; 当,b=-2时,原式=1-0=1。 22.如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:[来源:Zxxk.Com] (1)求抛物线的解析式; (2)若与轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点D,使得△ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由 注:抛物线的对称轴是 【答案】解:(1)∵抛物线y=x2+bx+c经过点(1,-4)和(-2,5), ∴,解得,。 ∴抛物线的解析式为。 (2)存在。 ∵抛物线的对称轴为, ∴根据轴对称的性质,点C关于的对称点D即为所求,此时, ∵AB=BA,AC=BD,BC=AD,∴△ABC≌△BAD(SSS)。[来源:学。科。网] 在中令,得,∴C(0,-3)。∴D(2,-3)。 23.已知一个等腰三角形的腰长为5,底边长为8,将该三角形沿底边上的高剪成两个三角形,用这个两个三角形能拼成几种平行四边形?请画出所拼的平行四边形,直接写出它们的对角线的长,并画出体现解法的辅助线 【答案】解:能拼成3种平行四边形,如图: 图1中,对角线的长为5; 图2中,对角线的长为3和; 24.在创建“绿色环境城市”活动中,某城市发布了一份2012年l至5月份空气质量抽样调查报告,随机抽查的30天中,空气质量的相关信息如下: 空气污 染指数 0~50 51~100 101~150 151~200 201~250 空气质 量指数 优 良 轻微 污染 轻度 污染 中度 污染[来源:学|科|网Z|X|X|K] 天数 6 15 3 2 请根据图表解答下列问题(结果取整数): (1)请将图表补充完整; (2)填空:根据抽样数据,估计该城市的空气质量级别为 的天数最多.[来源:Zxxk.Com] (3)请你根据抽样数据,通过计算,预测该城市一年(365天)中空气质量级别为优和良的天数共约有多少天 (4)请你根据数据显示,向有关部门提出一条创建“绿色环境城市”的建议. 【答案】解:(1)将图表补充完整如下: 空气污 染指数 0~50 51~100 101~150 151~200 201~250 空气质 量指数 优 良 轻微 污染 轻度 污染 中度 污染 天数 6 15 4 3 2 (2)良。 (3)∵365×(20%+50%)≈256(天), ∴预测该城市一年(365天)中空气质量级别为优和良的天数共约有256天。 (4)①采用“绿色化学”工艺,使工业原料尽可能转化为所需要的物质; ②推广使用乙醇汽油,减少有害气体的排放; ③推广使用卫生的一次性发泡塑料餐具,方便居民生活; ④增加绿化面积,建设生态园林城市。 等等(一条即可,答案不唯一)。 25.快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.下图表示的是两车之问的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息.解答下列问题: (1)直接写出快、慢两车的速度及A、B两站间的距离; (2)求快车从B 返回 A站时,y与x之间的函数关系式: (3)出发几小时,两车相距200千米?请直接写出答案 【答案】解:(1)快车的速度120千米/小时;慢车的速度80千米/小时;A、B两站间的距离1200千米。 (2)由(120-80)×(15-11)=160得点Q的坐标为(15,720)。 设直线PQ的解析式为,由P(11,880),Q(15,720)得 ,解得。∴直线PQ的解析式为。 设直线QH的解析式为,由Q(15,720),H(21,0)得 ,解得。∴直线QH的解析式为。 ∴快车从B 返回 A站时,y与x之间的函数关系式为 。 (3)出发5小时或7小时或小时,两车相距200千米。 26.如图①,△ABC中。AB=AC,P为底边BC上一点,PE⊥AB,PF⊥AC, CH⊥AB,垂足分别为E、F、H.易证PE+PF=CH.证明过程如下: (1)如图②,P为BC延长线上的点时,其它条件不变,PE、PF、CH又有怎样的数量网]关系?请写出你的猜想,并加以证明: (2)填空:若∠A=300,△ABC的面积为49,点P在直线BC上,且P到直线AC的距离为PF,当PF=3时,则AB边上的高CH= .点P到AB边的距离PE= 【答案】解:(1)PE=PF+CH。证明如下: ∵PE⊥AB,PF⊥AC, CH⊥AB, ∴。 ∵,∴。 又∵AB=AC,∴。 (2)7;4或10。 27.某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题: (1)求出足球和篮球的单价; (2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案? (3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多? 【答案】解:(1)设足球的单价为x元,则篮球的单价为x+20元, 根据题意,得8x+14(x+20)=1600, 解得x=60。 x+20=80。 答:足球的单价为60元,则篮球的单价为80元。 (2)设购进足球y个,则购进篮球50-y个。 根据题意,得,解得。 ∵y为整数,∴y=38,39,40。 当y=38,50-y=12;当y=39,50-y=11;当y=40,50-y=10。 ∴有三种方案: 方案一:购进足球38个,则购进篮球12个; 方案二:购进足球39个,则购进篮球11个; 方案一:购进足球40个,则购进篮球10个。 (3)商家售的利润:38(60-50)+12(80-65)=560(元); 商家售方案二的利润:39(60-50)+11(80-65)=555(元); 商家售方案三的利润:40(60-50)+10(80-65)=550(元)。 ∴ 第二次购买方案中,方案一商家获利最多。 28.如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题: (1)求直线AB的解析式; (2)若P为AB上一点,且;,求过点P的反比例函数的解析式; (3)在坐标平面内是否存在点Q,使得以A、P、O、Q为顶点的四边形是等腰梯形? 若存在,请直接写出点Q的坐标;若不存在,请说明理由. 【答案】解:(1)解x2-12x+32=0得x1=4,x2=8。 ∵OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB, ∴OA=8,OB=4。∴A(-8,0),B(0,4)。 设直线AB的解析式为,则 ,解得。 ∴直线AB的解析式为。 (2)过点P作PH⊥x轴于点H。 设P(x,y),由AH= x+8。 ∵,∴,即。 解得 x=-6。 ∵点P在上,∴。∴P(-6,1)。 设过点P的反比例函数的解析式为,则。∴。 ∴点P的反比例函数的解析式为。 (3)存在。点Q的坐标为(-2,1)或或。查看更多