中考数学专题复习练习：单元测试题(B)

中考数学专题复习练习：单元测试题(B)

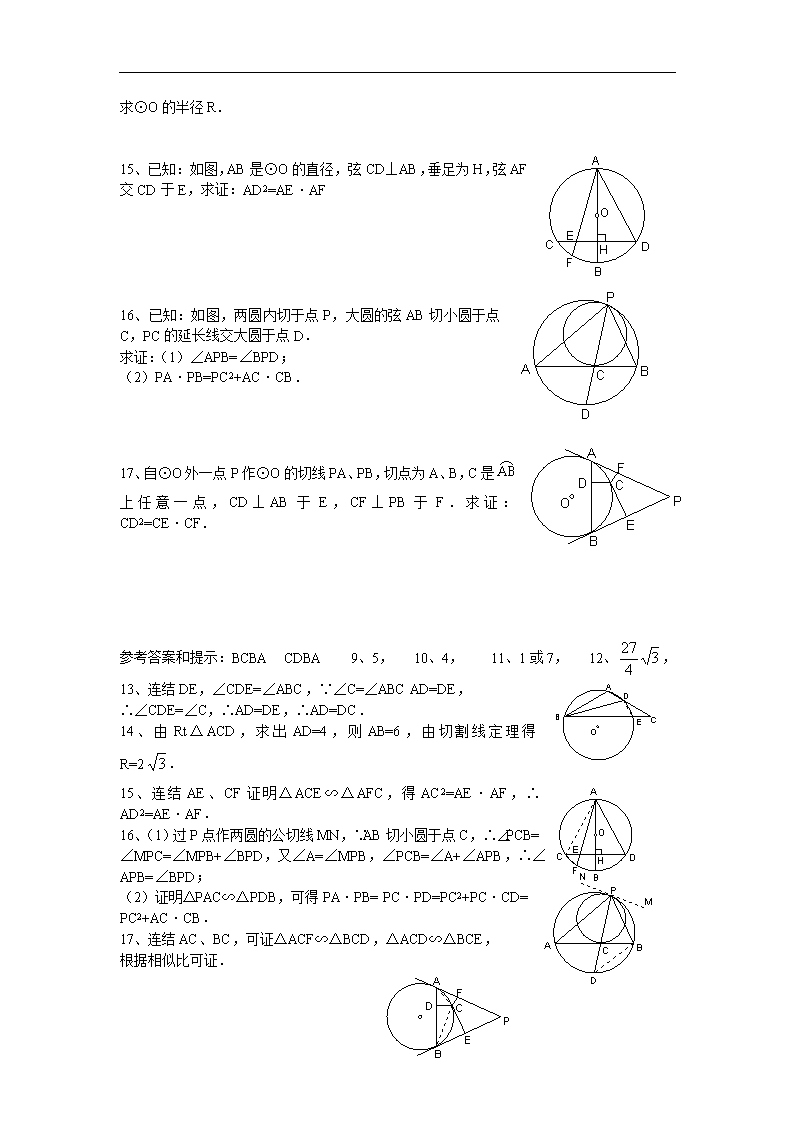
单元测试题(B) ‎ ‎ ‎ 班级 姓名 成绩 （时间：45分钟）‎ 一、选择题：(每题4分，共32分．每道题只有一个正确答案)‎ ‎1、如图，四边形ABCD内接于⊙O，若∠BOD=160°，则∠BCD=（ ）‎ ‎ (A)160° (B)100° (C)80° (D)20°‎ ‎2、C是半圆ACB上一点，AB是直径，且CD⊥AB于D，若AD＝8，DB＝3，则CD＝( )．‎ ‎(A)4 (B)6 (C)2 (D)4‎ ‎3、若两圆有三条公切线，则这两圆的位置关系是( )．‎ ‎(A)内切 (B)外切 (C)相交 (D)外离 ‎4、下列命题：(1)圆的两条平行弦所夹的弧相等；(2)垂直于圆的切线的直径必过切点；(3)圆内接正六边形的边长等于它的半径；(4)任意一个三角形只有一个外接圆，其中正确命题的个数是( )．‎ ‎ (A)4 (B)3 (C)2 (D)1‎ ‎5、若圆柱的底面半径为3，高为5，则圆柱的表面积为( )．‎ ‎ (A)30π (B) 36π ‎ (C) 48π (D) 60π ‎6、若一个圆锥的侧面积是底面积的2倍，则在这个圆锥的侧面展开图中，扇形圆心角的度数为( )．‎ ‎(A)60° (B)90° (C)120° (D)180°‎ ‎7、圆外切四边形ABCD的面积为20，AD与BC的边长之和为10，则圆的半径是（ ）‎ ‎ (A)1 (B)2 (C)4 (D)5‎ ‎8、在△ABC的内切圆分别和AB、BC、AC相切于D、E、F，则△DEF是（ ）‎ ‎(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)等边三角形 二、填空题：(每空4分，共16分)‎ ‎9、在半径是13的圆中，如果一条弦的长为24，那么这条弦的弦心距是 ．‎ ‎10、已知P为⊙O内一点，过点P的最长弦与最短弦分别为10cm，6cm，则OP= cm．‎ ‎11、在半径为5cm的圆中有两条弦AB、CD，若AB=6cm，CD=8cm，且AB∥CD，则AB与CD间的距离是 ．‎ ‎12、已知PA、PB分别切⊙O于A、B，∠APB=60°，若⊙O的半径为3，则△PAB的面积为 ．‎ 三、解答题：（16题12分，其它各题每题10分，共52分）‎ ‎13、如图，在△ABC中，AB=AC，BD平分∠ABC交AC于D，△ABC的外接圆交BC于E，求证：AD=EC．‎ ‎14、如图，AB切⊙O于B，AE过O点交⊙O于E、C，过C作⊙O切线交AB于D，若AD=2BD，AC=2．‎ 求⊙O的半径R．‎ ‎15、已知：如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，弦AF交CD于E，求证：AD2=AE·AF ‎16、已知：如图，两圆内切于点P，大圆的弦AB切小圆于点C，PC的延长线交大圆于点D．‎ 求证：（1）∠APB=∠BPD；‎ ‎（2）PA·PB=PC2+AC·CB．‎ ‎17、自⊙O外一点P作⊙O的切线PA、PB，切点为A、B，C是上任意一点，CD⊥AB于E，CF⊥PB于F．求证：CD2=CE·CF．‎ 参考答案和提示：BCBA CDBA 9、5， 10、4， 11、1或7， 12、，‎ ‎13、连结DE，∠CDE=∠ABC，∵∠C=∠ABC AD=DE，‎ ‎∴∠CDE=∠C，∴AD=DE，∴AD=DC．‎ ‎14、由Rt△ACD，求出AD=4，则AB=6，由切割线定理得R=2．‎ ‎15、连结AE、CF证明△ACE∽△AFC，得AC2=AE·AF，∴AD2=AE·AF．‎ ‎16、（1）过P点作两圆的公切线MN，∵AB切小圆于点C，∴∠PCB=∠MPC=∠MPB+∠BPD，又∠A=∠MPB，∠PCB=∠A+∠APB，∴∠APB=∠BPD；‎ ‎（2）证明△PAC∽△PDB，可得PA·PB= PC·PD=PC2+PC·CD= PC2+AC·CB．‎ ‎17、连结AC、BC，可证△ACF∽△BCD，△ACD∽△BCE，‎ 根据相似比可证．‎