初中数学中考总复习课件PPT：第12课时　反比例函数及其应用

初中数学中考总复习课件PPT：第12课时　反比例函数及其应用

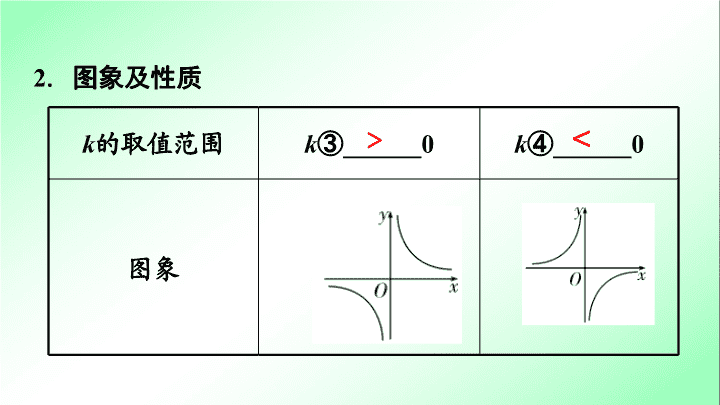
第一部分 夯实基础　提分多 第 三 单元 函数 第1 2 课时 反比例函数及其应用 1 ． 定义 ：形如 y ＝① _____( k 是常数， k ≠0) 的函数叫做反比例函数， k 叫做比例系数，反比例函数自变量的取值范围是② _________ 一切实数． 基础点 1 反比例函数的图象与性质 基础点巧练妙记 不为 0 的 2 ． 图象及性质 k 的取值范围 k ③______0 k ④ ______0 图象 < ＞ 图象特征 图象无限接近坐标轴，但不与坐标轴相交 增减性 在每一象限内， y 随 x 的增大而⑤ ______ ；第一象限 y 值大于第三象限 y 值 在每一象限内， y 随 x 的增大而⑥ ______ ；第二象限 y 值大于第四象限 y 值 对称性 关于原点成中心对称，关于直线 y ＝ x ， y ＝－ x 成轴对称 减小 增大            练 提 分 必 1 ．下列等式中， y 是 x 的反比例函数的是 ( 　　 ) 　　　　　　　　　　　　　　　　　 A ． y ＝ B . ＝ 3 C ． y ＝ 6 x ＋ 1 D ． x － y ＝ 2 A            练 提 分 必 2 ．当 x >0 时，函数 y ＝－ 5 x 的图象在 ( 　　 ) A ．第四象限 B ．第三象限 C ．第二象限 D ．第一象限 A            练 提 分 必 3 ．已知反比例函数 y ＝－ ，下列结论不正确的是 ( 　 ) A ．图象必经过点 ( － 1 ， 2) B ． y 随 x 的增大而增大 C ．图象在第二、四象限 D ．若 x >1 ，则－ 2 ＜ y ＜ 0 B            练 提 分 必 4 ．如果反比例函数 y ＝ 在各自象限内， y 随 x 的增大而减小，那么 m 的取值范围是 ( 　　 ) A. m ＜ 0 B. m ＞ 0 C. m ＜－ 1 D. m ＞－ 1 D     反比例函数值的大小比较   在函数 y ＝－ ( a 为常数 ) 的图象上有三点 ( － 3 ， y 1 ) ， ( － 1 ， y 2 ) ， (2 ， y 3 ) ，则函数值 y 1 ， y 2 ， y 3 的大小关系是 ( 　　 ) 　　　　　　　　　　　　　　　 A. y 2 ＜ y 3 ＜ y 1 B. y 3 ＜ y 2 ＜ y 1   C. y 1 ＜ y 2 ＜ y 3 D. y 3 ＜ y 1 ＜ y 2   6 失 分 点 D   错解： ∵ y ＝－ 是反比例函数 ， 且 k ＝－ ( a 2 ＋ 1) ＜ 0 ，∴ y 随 x 的增大而增大 ， ∵ － 3 ＜－ 1 ＜ 2, ∴ y 1 ＜ y 2 ＜ y 3 .       6 失 分 点       ∵ y ＝－ 是反比例函数，且 k ＝－( a 2 ＋1)＜0， ∴在第二象限内， y 随 x 的增大而增大，且 y ＞0；在第四象限内， y 随 x 的增大而增大，且 y ＜0，∴ y 2 ＞ y 1 ＞0， y 3 ＜0，∴ y 3 ＜ y 1 ＜ y 2 . 6 失 分 点 【 名师提醒 】 比较反比例函数值的大小时，要在同一象限内根据反比例函数的增减性判断，在不同象限内， y 值的大小根据符号特征进行判断． 基础点 2 反比例函数解析式中 k 的几何意义 ① k 的几何意义 如图，设 P ( x ， y ) 是反比例函数 y ＝图象上任意一点，过点 P 作 PM ⊥ x 轴于点 M ， PN ⊥ y 轴于点 N ，则 S 矩形 PMON ＝ PM · PN ＝ | y|·|x | ＝ | xy | ＝ | k |. ②计算与双曲线上的点有关的图形面积 S △AOP ＝ ⑦ ____ S △APB ＝ ⑧ ____ S △APP′ ＝ ⑨ ____ 2| k | 【 温馨提示 】 一般反比例函数与几何图形 ( 三角形、四边形 ) 结合，可直接利用 k 的几何意义求面积．若图形为不规则图形，则可将其分割，求面积之和．     5 ．如图，点 P 在反比例函数 y ＝ 的图象上， PA ⊥ x 轴于点 A ， PB ⊥ y 轴于点 B ，且△ APB 的面积为 2 ，则 k 等于 ( 　　 ) 　　　　　　　　　　　　　　　　　 A. － 4 B . － 2 C. 2 D. 4          练 提 分 必 第 5 题图 A 6. 如图，点 A 是反比例函数 y ＝ ( x ＜0)的图象上的一点，过点 A 作平行四边形 ABCD ，使点 B 、 C 在 x 轴上，点 D 在 y 轴上．已知平行四边形 ABCD 的面积为6，则k的值为(　　) A. 6 B. －6 C. 3 D. －3 练 提 分 必 B            练 提 分 必 7 ．如图，点 A 、 B 是双曲线 y ＝ 上的点，分别经过 A 、 B 两点向 x 轴、 y 轴作垂线段，若 S 阴影 ＝ 1 ，则 S 1 ＋ S 2 ＝ ( 　　 ) A. 2 　　　 B. 3 C. 4 　　　 D. 5 第 7 题图 C 基础点 3 反比例函数表达式的确定 1 ． 利用待定系数法求表达式 (1) 设出反比例函数的表达式 y ＝ ( k ≠ 0) ； (2) 找出满足反比例函数图象上的点 P ( a ， b ) ； (3) 将 P ( a ， b ) 代入表达式得 k ＝ ab ； (4) 确定反比例函数的表达式 y ＝ . 2 ．在具体问题中间根据 k 的几何意义通过求出相应三角形或四边形的面积求出 k 的值，从而求得表达式．    8 ．已知点 P ( － 4 ，－ 3) 在反比例函数 y ＝ ( k ≠0) 的图象上，则 k ＝ ________ ．           练 提 分 必 12     9 ．如图，反比例函数 y ＝ 的图象经过点 M ，矩形 OAMB 的面积为 4 ，则此反比例函数的解析 式为 __________ ．          练 提 分 必 第 9 题图 练习 1 　 已知函数 y ＝ 的图象如图所示，以下结论：① m <0 ；②在每个分支上 y 随 x 的增大而增大；③若点 A ( － 1 ， a ) 、点 B (2 ， b ) 在图象上，则 a < b ；④若点 P ( x ， y ) 在图象上，则点 P 1 ( － x ，－ y ) 也在图象上．其中正确的个数是 ( 　　 ) A. 4 个 B. 3 个 C. 2 个 D. 1 个　　　　　　　　　　 　　　　　　 重难点精讲优练 类型 1 反比例函数图象与性质 【 解析 】 ① 根据反比例函数的图象的两个分支分别位于二、四象限，可得 m ＜ 0 ，故正确；②在每个分支上 y 随 x 的增大而增大，故正确；③若点 A ( － 1 ， a ) 、点 B (2 ， b ) 在图象上，结合图象可知 a ＞ b ，故错误；④若点 P ( x ， y ) 在图象上，则点 P 1 ( － x ，－ y ) 也在图象上，故正确．故选 B . 练习 2 　已知点 A ( x 1 ， y 1 ) 、 B ( x 2 ， y 2 ) 是反比例函数 y ＝ － 图象上的两点，若 x 2 <0< x 1 ，则有 ( 　　 ) A . 0< y 1 < y 2 B . 0< y 2 < y 1 C . y 2 <0< y 1 D . y 1 <0< y 2 　　　　　　 　　　　　　 D 【解析】 ∵ k ＝－3＜0，∴双曲线位于二、四象限．∵ x 2 ＜0＜ x 1 ，∴ y 2 ＞0， y 1 ＜0.∴ y 1 ＜0＜ y 2 . 练习 3 　如图，点 A 在函数 y ＝ ( x >0) 的图象上，且 OA ＝ 4 ，过点 A 作 AB ⊥ x 轴于点 B ，则△ ABO 的周长为 ________ ． 【解析】 ∵ 点 A 在函数 y ＝ ( x >0) 的图象上，∴设点 A 的坐标为 (n ， )(n ＞ 0) ．在 Rt △ ABO 中，∠ ABO ＝ 90° ， OA ＝ 4 ，∴ OA 2 ＝ AB 2 ＋ OB 2 ，又∵ AB · OB ＝ · n ＝ 4 ，∴ ( AB ＋ OB ) 2 ＝ AB 2 ＋ OB 2 ＋ 2 AB · OB ＝ 4 2 ＋ 2×4 ＝ 24 ，∴ AB ＋ OB ＝ 2 或 AB ＋ OB ＝－ 2 ( 舍去 ) ．∴ C △ AOB ＝ AB ＋ OB ＋ OA ＝ 2 ＋ 4. 类型 2 反比例函数与一次函数结合 例 　如图，已知点 A ( － 4 ， n ) ，点 B (2 ，－ 4) 是一次函数 y ＝ kx ＋ b 的图象和反比例函数 y ＝ 的图象的两个交点． (1) 求反比例函数和一次函数的解析式； (2) 求直线 AB 与 x 轴的交点 C 的坐标及△ AOB 的面积； 例题图 (3) 求方程 kx ＋ b － ＝ 0 的解； (4) 根据图象直接写出不等式 kx ＋ b － ＜ 0 的解集． 解 ： (1)∵点 B (2，－4)在函数 y ＝ 的图象上， ∴ m ＝－8， ∴反比例函数的解析式为 y ＝－ ， ∵点 A (－4， n )在函数 y ＝－ 的图象上， ∴ n ＝2，∴ A (－4，2)， ∵ y ＝ kx ＋ b 经过点 A ( － 4 ， 2) ，点 B (2 ，－ 4) ， ∴ ，解得 ， ∴一次函数的解析式为 y ＝－ x － 2 ； － 4 k ＋ b ＝ 2 2 k ＋ b ＝－ 4 k ＝－ 1 b ＝－ 2 (2) ∵ C 是直线 AB 与 x 轴的交点， ∴当 y ＝ 0 时， x ＝－ 2 ， ∴ C ( － 2 ， 0) ，即 OC ＝ 2 ， ∴ S △ AOB ＝ S △ ACO ＋ S△ BCO ＝ OC•yA ＋ OC •|y B | ＝ ×2×2 ＋ ×2×4 ＝ 6 ； (3) 方程 kx ＋ b － ＝0的解，即为一次函数 y ＝ kx ＋ b 的图象和反比例函数 y ＝ 的图象的交点的横坐标，则 x 1 ＝－4， x 2 ＝2； (4) 不等式 kx ＋ b － <0的解集即为一次函数 y ＝ kx ＋ b 图象在反比例函数 y ＝ 图象下方时 x 的取值范围，从图象可以看出：不等式的解集为－ 4< x <0 或 x >2.   对于一次函数与反比例函数的综合题 ， 常涉及以下几个方面： 1 ． 求交点坐标：联立方程组求解或利用反比例函数对称性求解． 2 ． 确定函数表达式：将交点坐标代入 y ＝ 可求 k ， 由    导 方 法 指 两交点 A ， B 坐标利用待定系数法可求 y ＝ ax ＋ b .          3 ．求不等式解集： (1) 对于不等式 ax ＋ b > 的解集，即为一次函数图象在反比例函数图象上方时 x 的取值范围； (2) 对于不等式 ax ＋ b < 的解集，即为反比例函数图象位于一次函数图象上方时 x 的取值范围；    导 方 法 指 4．在涉及与面积有关的问题时，要善于把点的横、纵坐标转化为图形的边长，对于不容易直接求的面积往往可转化为规则易计算的三角形面积的和或差，同时也要注意系数 k 的几何意义的应用． 导 方 法 指 练习 4 　如果一个点的横、纵坐标均为整数，那么我们称这个点为格点．如图， A 、 B 两点在反比例函数 y ＝ ( x ＞ 0) 的图象上，则图中阴影部分 ( 不包括边界 ) 所含格点的个数为 ( 　　 ) 　　　　　　　　　　　　　　　　　 A . 2 个 B . 3 个 C . 4 个 D . 5 个 练习 4 题图 【解析】 把点 A (1，6)代入 y ＝ ，得 m ＝1×6＝6，∴反比例函数的解析式为 y 1 ＝ ，设直线 AB 的解析式为 y 2 ＝ ax ＋ b ，把点 A (1，6)，点 B (6，1)代入得， 解得 a ＋ b ＝6 6 a ＋ b ＝1 a ＝-1 b ＝7 ∴直线 AB 的解析式为 y 2 ＝－ x ＋7.当 x ＝2， y 1 ＝ ＝3， y 2 ＝－ x ＋7＝5；当 x ＝3， y 1 ＝ ＝2， y 2 ＝－ x ＋7＝4；当 x ＝4， y 1 ＝ ＝ ， y 2 ＝－ x ＋7＝3；当 x ＝5， y 1 ＝ ＝ ， y 2 ＝－ x ＋7＝2.∴图中阴影部分(不包括边界)所含格点的有：(2，4)，(3，3)，(4，2)，共3个．