鄂尔多斯专版2020中考数学复习方案基础解答组合限时练06试题

鄂尔多斯专版2020中考数学复习方案基础解答组合限时练06试题

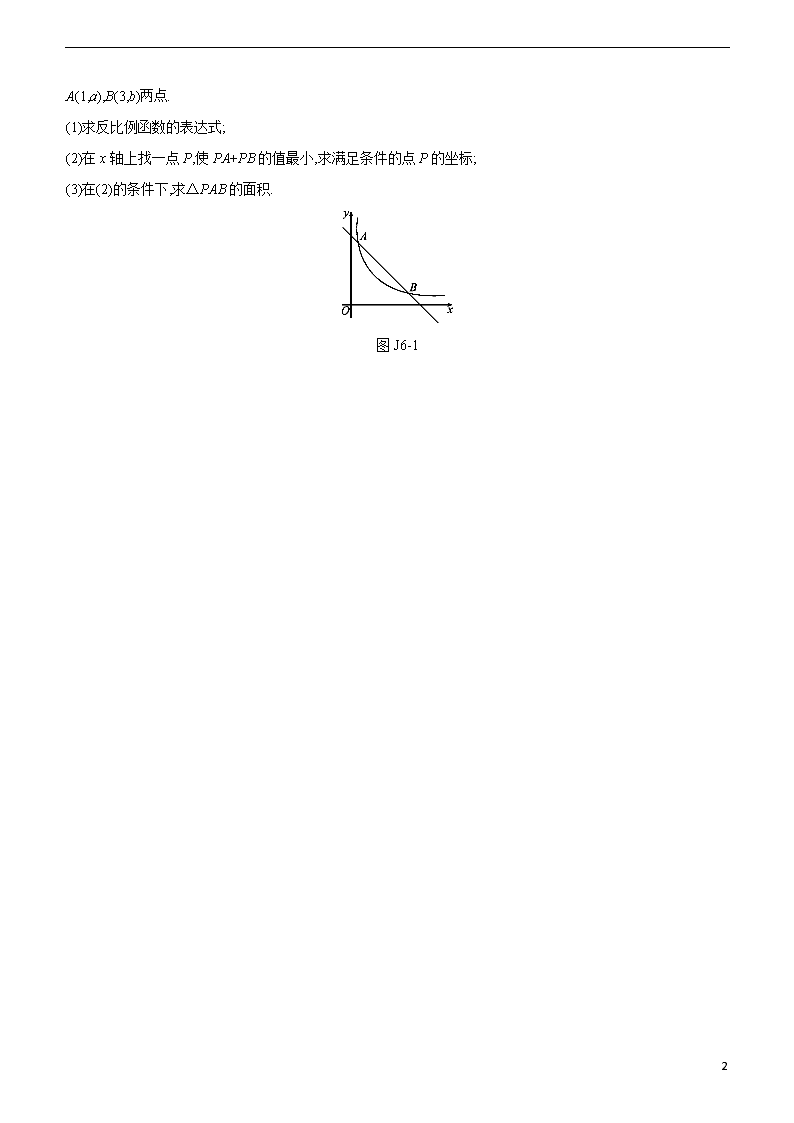
基础解答组合限时练(六)‎ 限时:20分钟　满分:20分 ‎17.(8分)(1)解不等式组:‎3-2(x-1)>0,‎x+3‎‎2‎‎-1≤x,‎并写出它的整数解.‎ ‎(2)先化简1-‎1‎x-1‎÷x‎2‎‎-4x+4‎x‎2‎‎-1‎,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.‎ ‎18.(4分)计算:(3.14-π)0+|‎2‎-1|-2cos45°+(-1)2020.‎ 4‎ ‎19.(8分)如图J6-1,一次函数y=-x+4的图象与反比例函数y=kx(k为常数,且k≠0)在第一象限内的图象交于A(1,a),B(3,b)两点.‎ ‎(1)求反比例函数的表达式;‎ ‎(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;‎ ‎(3)在(2)的条件下,求△PAB的面积.‎ 图J6-1‎ 4‎ ‎【参考答案】‎ ‎17.解:(1)解不等式3-2(x-1)>0,得x<‎5‎‎2‎.‎ 解不等式x+3‎‎2‎-1≤x,得x≥1.‎ ‎∴不等式组的解集为1≤x<‎5‎‎2‎,其整数解为1,2.‎ ‎(2)原式=x-1‎x-1‎‎-‎‎1‎x-1‎·‎‎(x+1)(x-1)‎‎(x-2‎‎)‎‎2‎ ‎=x-2‎x-1‎·‎‎(x+1)(x-1)‎‎(x-2‎‎)‎‎2‎ ‎=x+1‎x-2‎.‎ 当x满足-2≤x≤2且为整数时,若使分式有意义,只能取0或-2.‎ 当x=0时,原式=-‎1‎‎2‎;当x=-2时,原式=‎1‎‎4‎.‎ ‎18.解:原式=1+‎2‎-1-2×‎2‎‎2‎+1=1.‎ ‎19.解:(1)把(1,a)代入y=-x+4,‎ 得a=-1+4=3.∴A(1,3).‎ 将(1,3)代入y=kx,得k=3.‎ ‎∴反比例函数的表达式为y=‎3‎x.‎ ‎(2)把B(3,b)代入y=-x+4,得b=1.‎ ‎∴点B的坐标为(3,1).‎ 如图,作点B关于x轴的对称点D(3,-1),交x轴于点C,连接AD,交x轴于点P,连接PB,此时PA+PB的值最小,‎ 设直线AD的解析式为y=mx+n.‎ 把A,D两点的坐标代入,得m+n=3,‎‎3m+n=-1.‎ 解得m=-2,‎n=5.‎ ‎∴AD所在直线的解析式为y=-2x+5.‎ 令y=0,得x=‎5‎‎2‎.‎ 4‎ ‎∴点P的坐标为‎5‎‎2‎‎,0‎.‎ ‎(3)S△PAB=S△ABD-S△PBD ‎=‎1‎‎2‎×2×(3-1)-‎1‎‎2‎×2×3-‎‎5‎‎2‎ ‎=2-‎1‎‎2‎=1.5.‎ 4‎