中考数学模拟分类汇编-实验应用型问题

中考数学模拟分类汇编-实验应用型问题

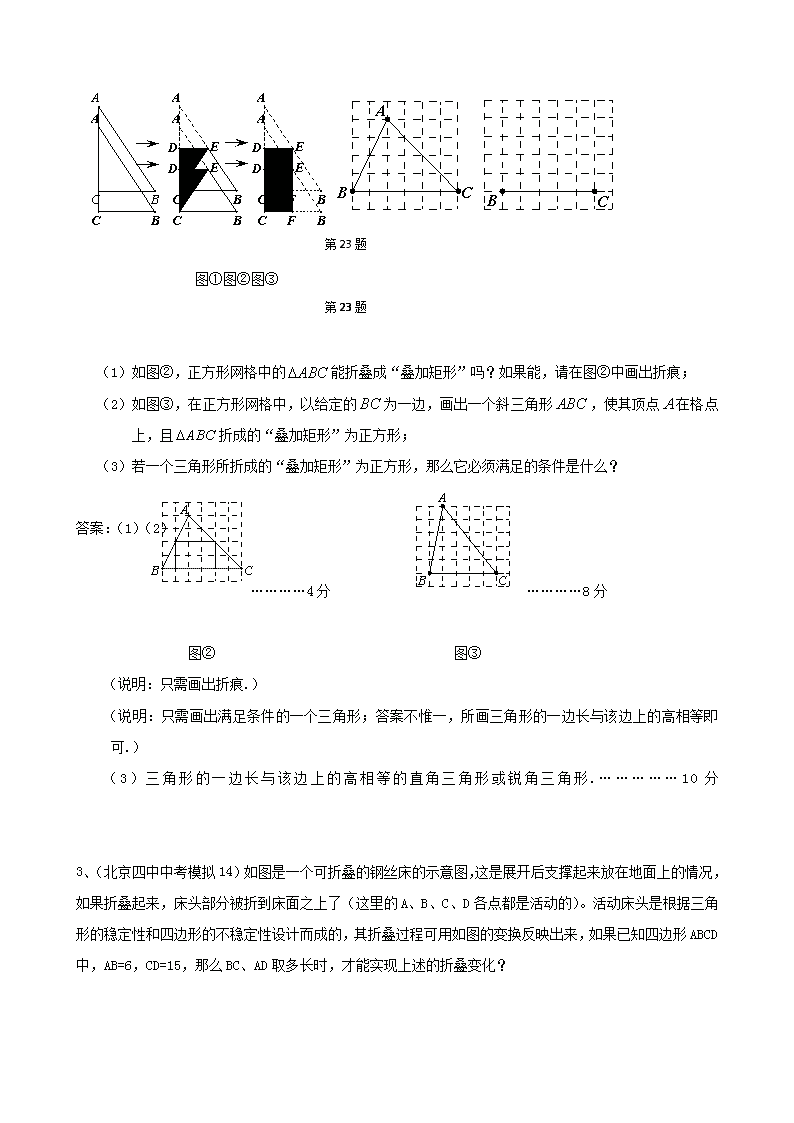
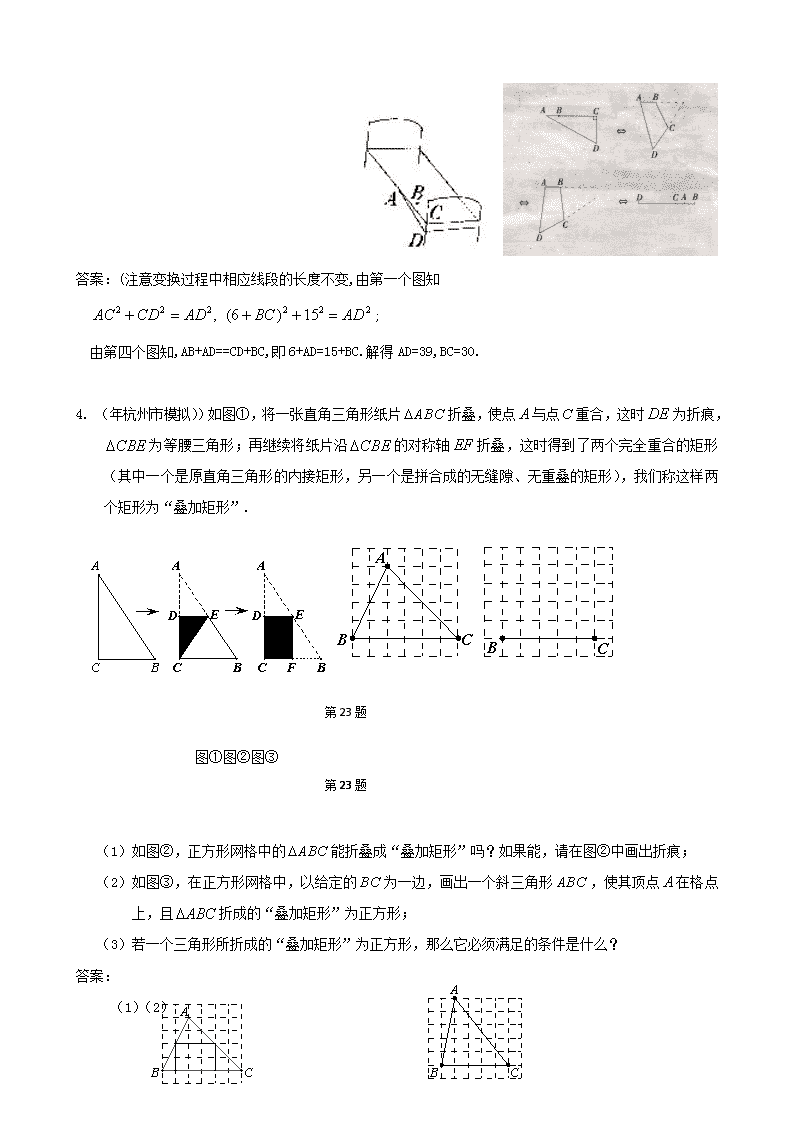
实验应用型问题填空题1、（赵州二中九年七班模拟）用含角的两块同样大小的直角三角板拼图形，下列五种图形：①平行四边形，②菱形，③矩形，④直角梯形，⑤等边三角形。其中可以被拼成的图形是（只填正确答案的序号）。答案：①③⑤解答题1．（年重庆江津区七校联考）我市某销售商2009年从果农处共收购并销售了100吨荔枝，平均收购价为6元/千克，平均售出价为7元/千克。2010年适当提高了收购价，同时，为适应市场需求，用2009年销售荔枝赚得的年利润的50%作为投资，购买了一些荔枝精包装的加工设备和材料，荔枝精加工后，销售价提高部分没有超过原销售价的一半。由于对荔枝的精选，2010年的购销量有所减少。经过前期市场调查表明，同2009年相比，每吨平均收购价增加的百分数︰每吨平均销售价增加的百分数︰年购销量减少的百分数＝2.5︰5︰1。⑴该销售商2009年的年利润为多少？⑵若该销售商预计2010年所获的年利润，除收回购买荔枝精包装的加工设备和材料的投资外，还赚了22万元的利润，问2010年他们购销量减少的百分数为多少?答案：(1)(7-6)×100×1000=100000(元)(2)设2010年购销量减少的百分数为，由题意得：化简：解得：(舍去)=10%2．（年杭州市西湖区模拟）如图①，将一张直角三角形纸片折叠，使点与点重合，这时为折痕，为等腰三角形；再继续将纸片沿的对称轴折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”. 第23题图①图②图③第23题第23题（1）如图②，正方形网格中的能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；（2）如图③，在正方形网格中，以给定的为一边，画出一个斜三角形，使其顶点在格点上，且折成的“叠加矩形”为正方形；（3）若一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？答案：（1）（2）…………4分…………8分图②图③（说明：只需画出折痕.）（说明：只需画出满足条件的一个三角形；答案不惟一，所画三角形的一边长与该边上的高相等即可.）（3）三角形的一边长与该边上的高相等的直角三角形或锐角三角形.……………10分3、（北京四中中考模拟14）如图是一个可折叠的钢丝床的示意图，这是展开后支撑起来放在地面上的情况，如果折叠起来，床头部分被折到床面之上了（这里的A、B、C、D各点都是活动的）。活动床头是根据三角形的稳定性和四边形的不稳定性设计而成的，其折叠过程可用如图的变换反映出来，如果已知四边形ABCD中，AB=6，CD=15，那么BC、AD取多长时，才能实现上述的折叠变化？ 答案：(注意变换过程中相应线段的长度不变,由第一个图知;由第四个图知,AB+AD==CD+BC,即6+AD=15+BC.解得AD=39,BC=30.4.（年杭州市模拟））如图①，将一张直角三角形纸片折叠，使点与点重合，这时为折痕，为等腰三角形；再继续将纸片沿的对称轴折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”.第23题图①图②图③第23题第23题（1）如图②，正方形网格中的能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；（2）如图③，在正方形网格中，以给定的为一边，画出一个斜三角形，使其顶点在格点上，且折成的“叠加矩形”为正方形；（3）若一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？答案：（1）（2） 图②图③（说明：只需画出折痕.）（说明：只需画出满足条件的一个三角形；答案不惟一，所画三角形的一边长与该边上的高相等即可.）（3）三角形的一边长与该边上的高相等的直角三角形或锐角三角形.