北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 3 一节一练正方形的性质与判定

北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 3 一节一练正方形的性质与判定

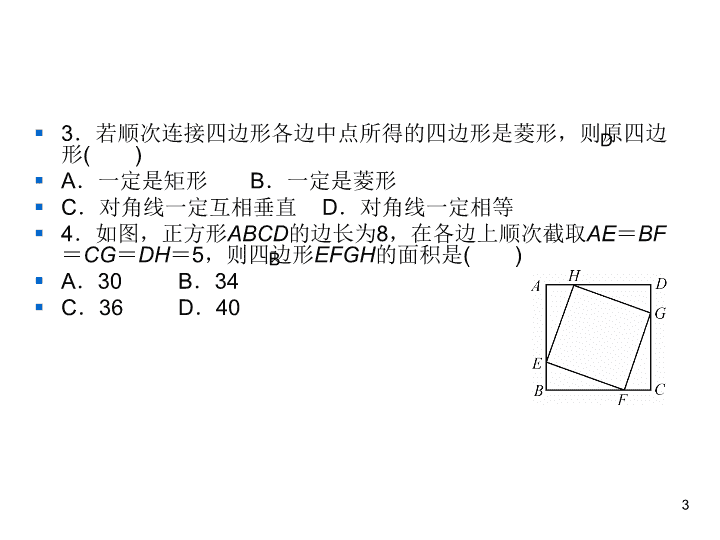
第一章　特殊平行四边形3　正方形的性质与判定 1．下列命题中，真命题是()A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形2．矩形各内角平分线围成的四边形是()A．平行四边形B．矩形C．菱形D．正方形2基础过关CD 3．若顺次连接四边形各边中点所得的四边形是菱形，则原四边形()A．一定是矩形B．一定是菱形C．对角线一定互相垂直D．对角线一定相等4．如图，正方形ABCD的边长为8，在各边上顺次截取AE＝BF＝CG＝DH＝5，则四边形EFGH的面积是()A．30B．34C．36D．403DB 5．【贵州黔东南中考】如图，正方形ABCD中，E为AB中点，FE⊥AB，AF＝2AE，FC交BD于O，则∠DOC的度数为()A．60°B．67.5°C．75°D．54°6．如图，正方形ABCD中，AB＝1，点P是对角线AC上的一点，分别以AP、PC为对角线作正方形，则这两个小正方形的周长的和是_________.4A4 7．如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝5，F为DE的中点．若△CEF的周长为18，则OF的长为_________.58．如图，已知方格纸中有4个相同的正方形，则∠1＋∠2＋∠3＝____________.135° 9．如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，得到下面四个结论：①OA＝OD；②AD⊥EF；③当∠BAC＝90°时，四边形AEDF是正方形；④AE2＋DF2＝AF2＋DE2.其中正确的是___________.(填序号)6②③④ 10．如图，在△ABC中，∠ACB＝90°，CD平分∠ACB，DE∥BC，DF∥AC，分别交AC、BC于点E、F.求证：四边形DECF是正方形．证明：∵DE∥BC，DF∥AC，∴四边形DECF是平行四边形．∵∠ACB＝90°，∴四边形DECF为矩形．∵CD平分∠ACB，∴∠DCF＝∠ECD＝∠CDF＝45°，∴DF＝CF，∴四边形DECF为正方形．7 11．【四川广安中考】如图，四边形ABCD是正方形，E、F分别是AB、AD上的一点，且BF⊥CE，垂足为G，求证：AF＝BE.8 9能力提升B 10A 14．将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和为()A．2cm2B．4cm2C．6cm2D．8cm211B 15．已知正方形ABCD的边长为4，点E、F分别在AD、DC上，AE＝DF＝1，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为___________.122.5 16．【山东聊城中考】如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，…，以此类推，则正方形OB2015B2016C2016的顶点B2016的坐标是_________________.13(21008,0) 17．如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F.(1)判断OE与OF的大小关系，并说明理由；(2)当点O运动到何处时，四边形AECF是矩形？并说明理由；(3)在(2)的条件下，当△ABC满足什么条件时，四边形AECF是正方形？直接写出答案，不需说明理由．14 15 18．如图，在正方形ABCD中，E是BD上一点，AE的延长线交CD于点F，交BC的延长线于点G，M是FG的中点．(1)求证：①∠1＝∠2；②EC⊥MC；(2)试问当∠1等于多少度时，△ECG为等腰三角形？请说明理由．16思维训练 (1)证明：①∵四边形ABCD是正方形，∴∠ADE＝∠CDE，AD＝CD.又∵DE＝DE，∴△ADE≌△CDE，∴∠1＝∠2.②∵AD∥BG，∴∠1＝∠G.∵M是FG的中点，∴MC＝MG＝MF，∴∠G＝∠MCG.又∵∠1＝∠2，∴∠2＝∠MCG.∵∠FCG＝∠MCG＋∠FCM＝90°，∴∠ECM＝∠2＋∠FCM＝90°，∴EC⊥MC.(2)解：当∠1＝30°时，△ECG为等腰三角形．理由如下：∵∠1＝∠2＝∠G，∴在△ECG中，∠G＋∠CEG＋∠2＋∠FCG＝180°，即∠CEG＝90°－2∠1.当∠1＝30°时，∠CEG＝90°－60°＝30°，∴∠CEG＝∠1，∴△ECG为等腰三角形．17