人教版九年级上册数学同步练习课件-期末复习4圆
期末复习期末复习4圆
1.垂径定理:(1)垂直于弦的直径________弦,并且________弦所对的两条弧;(2)推论:________弦(____________)的直径垂直于弦,并且__________弦所对的两条弧.2.在同圆或等圆中,两个__________,两个__________,两条______,两条______中有一组量相等,它们所对应的其余各组量也相等.3.圆周角定理:(1)一条弧所对的圆周角等于它所对的圆心角的________.(2)推论:①同弧或等弧所对的圆周角________;②半圆(或直径)所对的圆周角是________,90°的圆周角所对的弦是________.2知识整理平分平分平分不是直径平分圆心角圆周角弦弧一半相等直角直径
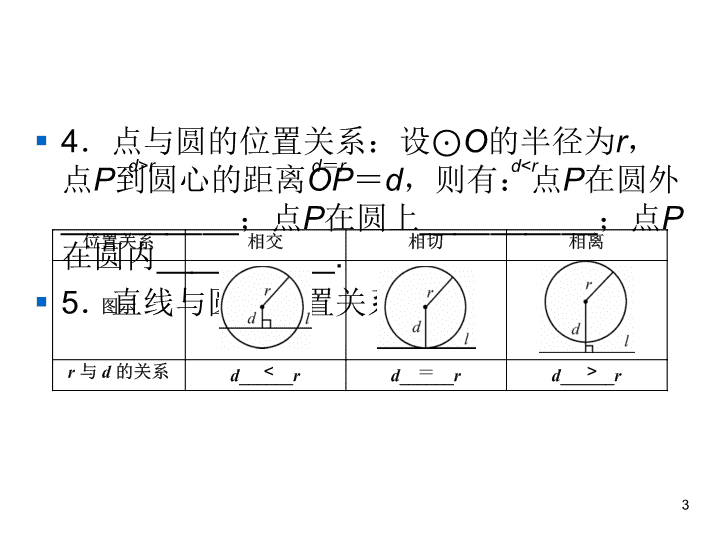
4.点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外__________;点P在圆上__________;点P在圆内__________.5.直线与圆的位置关系:3d>rd=rd
6.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长________,这一点和圆心的连线________两条切线的夹角.7.正多边形与圆:一个正多边形的外接圆的________叫做这个正多边形的中心,外接圆的________叫做正多边形的半径,正多边形每一边所对的__________叫做正多边形的中心角,中心到正多边形的一边的__________叫做正多边形的边心距.4相等平分圆心半径圆心角距离
8.弧长与扇形面积:在半径为R的圆中,n°的圆心角所对的弧长是_______,n°的圆心角所对应的扇形面积是________,弧长为l的扇形面积是__________.9.圆锥的侧面积与全面积:圆锥的母线l,圆锥的高h,底面圆的半径r,则圆锥的侧面积S=__________;圆锥的全面积S全=________________.5πlrπr2+πlr
6专题集训C
2.⊙O的直径为10,弦AB=6,P是弦AB上一动点,则OP的取值范围是______________.3.如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.解:∵AB为⊙O直径,∴∠ADB=90°.∵同圆或等圆中,相同的弧所对应的圆周角相等,且∠ACD=25°,∴∠B=25°,∴∠BAD=90°-∠B=65°.74≤OP≤5
8
9
6.如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.(1)求证:DC是⊙O的切线;(2)若AE=1,ED=3,求⊙O的半径.10(1)略(2)解:连接DO.设⊙O的半径为R,则OD=R,OE=R+1.∵CD是⊙O的切线,∴∠EDO=90°,∴ED2+OD2=OE2,∴32+R2=(R+1)2,解得R=4,∴⊙O的半径为4.
7.在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB、AC相交于点D、E,过点D作DF⊥AC,垂足为点F.(1)求证:DF是⊙O的切线;(2)分别延长CB、FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.11
12
★集训3物体运动的路径长8.已知一个圆心角为270°的扇形工件,未搬动前如图所示,A、B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A、B两点再次触地时停止,若扇形的半径为3m,则圆心O所经过的路线长是_______m.(结果保留π)136π
9.如图,一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,那么B点从开始至结束所走过的路径长度为______.14
15
16C
12.如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H.则图中阴影部分的面积为__________.172π+4
13.如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中阴影部分的面积为____________.18
★集训5圆中的分类讨论14.如图,A、B是⊙O上的两点,C是⊙O上不与A、B重合的任意一点,如果∠AOB=140°,那么∠ACB的度数为()A.70°B.110°C.140°D.70°或110°19D
15.如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为__________________________.20(7,4)或(6,5)或(1,4)
21
22达标集训CD
3.已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,PA=,那么点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.无法确定4.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定()A.与x轴相离,与y轴相切B.与x轴,y轴都相离C.与x轴相切,与y轴相离D.与x轴,y轴都相切23DA
5.如图,点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是()24B
25C
26A
27D
二、填空题(每小题4分,共16分)9.如图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为__________.28(2,0)
10.如图,在△ABC中,∠A=90°,AB=AC=2cm,⊙A与BC相切于点D,则⊙A的半径长为______cm.29
11.如图,∠AOB=30°,OM=6,那么以M为圆心,4为半径的圆与直线OA的位置关系是________.30相交12.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC=______cm.
31
32
14.(15分)如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.(1)求证:DE是⊙O的切线;(2)若△ABC的边长为4,求EF的长度.33
15.(15分)如图,直角坐标系中,已知A(-8,0)、B(0,6),点M在线段AB上.(1)如图1,如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由;(2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标.34
35
36