- 2021-11-01 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华东师大版七年级上册数学单元测试题
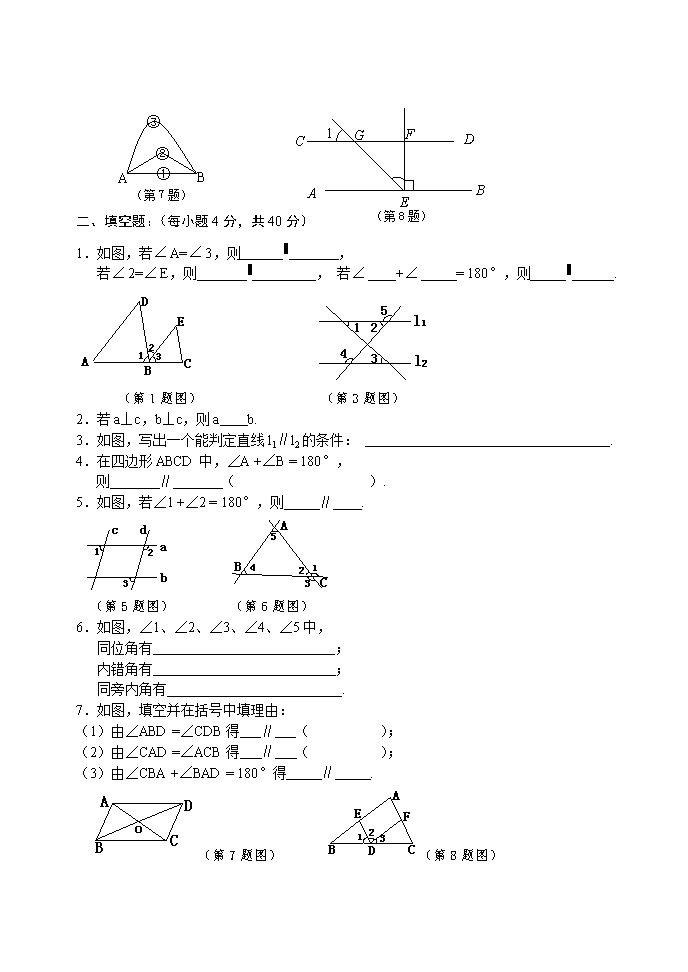
密 线 七年级单元试题·数学 一.选择题; 1.在同一平面内,两条直线可能的位置关系是 ( ) (A) 平行. (B) 相交. (C) 相交或平行. (D) 垂直. 2.判定两角相等,不正确的是 ( ) (A) 对顶角相等. (B) 两直线平行,同位角相等. (C) ∵∠1=∠2,∠2=∠3,∴∠1=∠3. (D) 两条直线被第三条直线所截,内错角相等. 3.两个角的两边分别平行,其中一个角是60°,则另一个角是 ( ) (A)60°. (B)120°. (C) 60°或120°. (D) 无法确定. 4.下列语句中正确的是( ) (A)不相交的两条直线叫做平行线. (B)过一点有且只有一条直线与已知直线平行. (C)两直线平行,同旁内角相等. (D)两条直线被第三条直线所截,同位角相等. 5.下列说法正确的是( ) (A)垂直于同一直线的两条直线互相垂直. (B)平行于同一条直线的两条直线互相平行. (C)平面内两个角相等,则他们的两边分别平行. (D)两条直线被第三条直线所截,那么有两对同位角相等. 6.骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是 ( ) A. B. C. D. 7.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是 ( ) A.因为它最直. B.两点确定一条直线. C.两点间的距离的概念. D.两点之间,线段最短. 8.如图,,于,交于,GE平分∠AEF,则是( ) A. B. C. D. 1 A B C D E F (第8题) G ③ ① ② A B (第7题) 二、填空题:(每小题4分,共40分) 1.如图,若A=3,则 ∥ , 若2=E,则 ∥ , 若 + = 180°,则 ∥ . (第1题图) (第3题图) 2.若a⊥c,b⊥c,则a b. 3.如图,写出一个能判定直线l1∥l 2的条件: . 4.在四边形ABCD中,∠A +∠B = 180°, 则 ∥ ( ). 5.如图,若∠1 +∠2 = 180°,则 ∥ . (第5题图) (第6题图) 6.如图,∠1、∠2、∠3、∠4、∠5中, 同位角有 ; 内错角有 ; 同旁内角有 . 7.如图,填空并在括号中填理由: (1)由∠ABD =∠CDB得 ∥ ( ); (2)由∠CAD =∠ACB得 ∥ ( ); (3)由∠CBA +∠BAD = 180°得 ∥ . (第7题图) (第8题图) 8.如图,推理填空: (1)∵∠A =∠ (已知), ∴AC∥ED( ); (2)∵∠2 =∠ (已知), ∴AC∥ED( ); (3)∵∠A +∠ = 180°(已知), ∴AB∥FD( ); (4)∵∠2 +∠ = 180°(已知), ∴AC∥ED( ); O A B C 1 (第9题) 9.如图,O为直线AB上一点, ∠COB=26°30′,则∠1= 度. 10.如图是一组有规律的图案,第1个 图案由6个基础图形组成,第2个图案由11个基础图形组成,……,第(n是正整数)个图案中由 个基础图形组成.(用含n的代数式表示) …… (第10题) (3) (2) (1) 三、解答题:(每小题7分,共56分) 11.长方体的主视图与左视图如图所示(单位:cm), (1)根据图中的数据画出它的俯视图,并求出俯视图的面积; (第11题) _ 2 _ 3 _ 4 _ 2 _ 主视图 _ 左视图 (2)求这个长方体的体积. 12.已知:点P是直线MN外一点,点A、B、C是直线MN上三点, 分别连接PA、PB、PC. (1)通过测量的方法,比较PA、PB、PC的大小,直接用“>”连接. (第18题) P N M A B C (2)在直线MN上能否找到一点D,使PD的长度最短,如果有,请在图中作出线段PD,并说明它的理论依据.如果没有,请说明理由. 13.如图已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请完善说明过程,并在括号 内填上相应依据: ∵AD∥BC(已知) A E D B F C 1 3 4 2 (第19题) ∴∠1=∠3 ( ), ∵∠1=∠2(已知) ∴∠ 2=∠3 ( ), ∴____∥__ _( ), ∴∠3+∠4=180°( ) . 14.如图,∠D =∠A,∠B =∠FCB,求证:ED∥CF. 15.如图,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由. 16.如图,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME.求证:AB∥CD, MP∥NQ. 17.已知:如图AD∥BE,∠1=∠2,求证:∠A=∠E.(7分) 18.已知:如图,CD平分∠ACB,AC∥DE,CD∥EF,试说明EF平分∠DEB.(8分) 六、选做题:(每小题10分,共30分,总分不满120分时可计入总分) 19、某校校长在国庆节带领该校市级“三好学生”外出旅游,甲旅行社说“如果校长买一张票,则其余学生可享受半价优惠”,乙旅行社说“包括校长在内全部按票价的6折优惠”(即按票的60%收费)。现在全票价为240元,学生数为5人,请算一下哪家旅行社优惠?你喜欢哪家旅行社?如果是一位校长,两名学生呢?(7分) 20.某种铂金饰品在甲、乙两个商店销售.甲商店标价477元/克,按标价出售,不优惠.乙商店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.若购买的铂金饰品重量为x克. (1)分别列出到甲、乙商店购买该种铂金饰品所需的费用(用含x的代数式表示); (2)李阿姨要买一条重量10克的此种铂金饰品,到哪个商店购买最合算? 21.一副直角三角板(其中一个三角板的内角是45°,45°,90°,另一个是 30°,60°,90°) (1)如图①放置,AB⊥AD,∠CAE= ,BC与AD的位置关系是 ; (2)在(1)的基础上,再拿一个30°,60°,90°的直角三角板,如图②放置,将AC′边和AD边重合, AE是∠CAB′的角平分线吗,如果是,请加以说明,如果不是,请说明理由. (3)根据(1)(2)的计算,请解决下列问题: 如图③∠BAD=90°,∠BAC=∠FAD=20°,将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由. (4)如果将图③中的∠BAC=∠FAD=(是锐角),其它条件不变,那么(3)问中的结论还成立吗?只需回答是还是不是,不需要说明理由. B A C F D (第7题) (图③) E C’ B A C D (第7题) E (图②) B A C E D (第7题) (图①) (第7题)查看更多