北师大版八年级数学（下册）期末复习专项测试卷（三）（附参考答案）

北师大版八年级数学（下册）期末复习专项测试卷（三）（附参考答案）

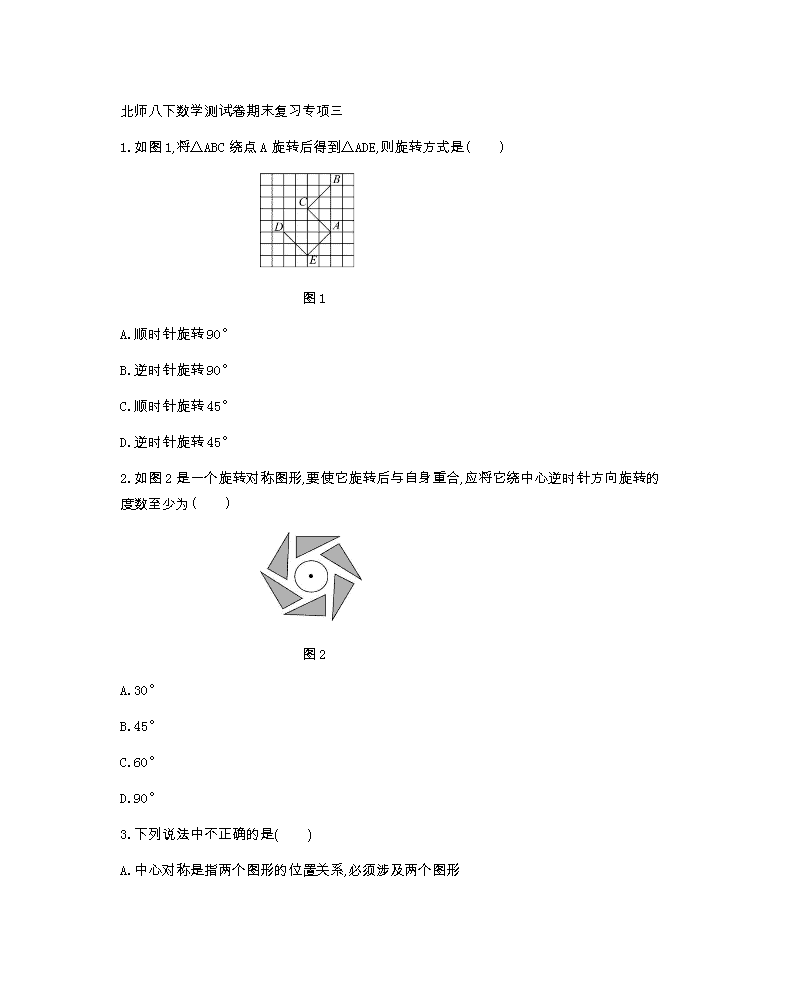
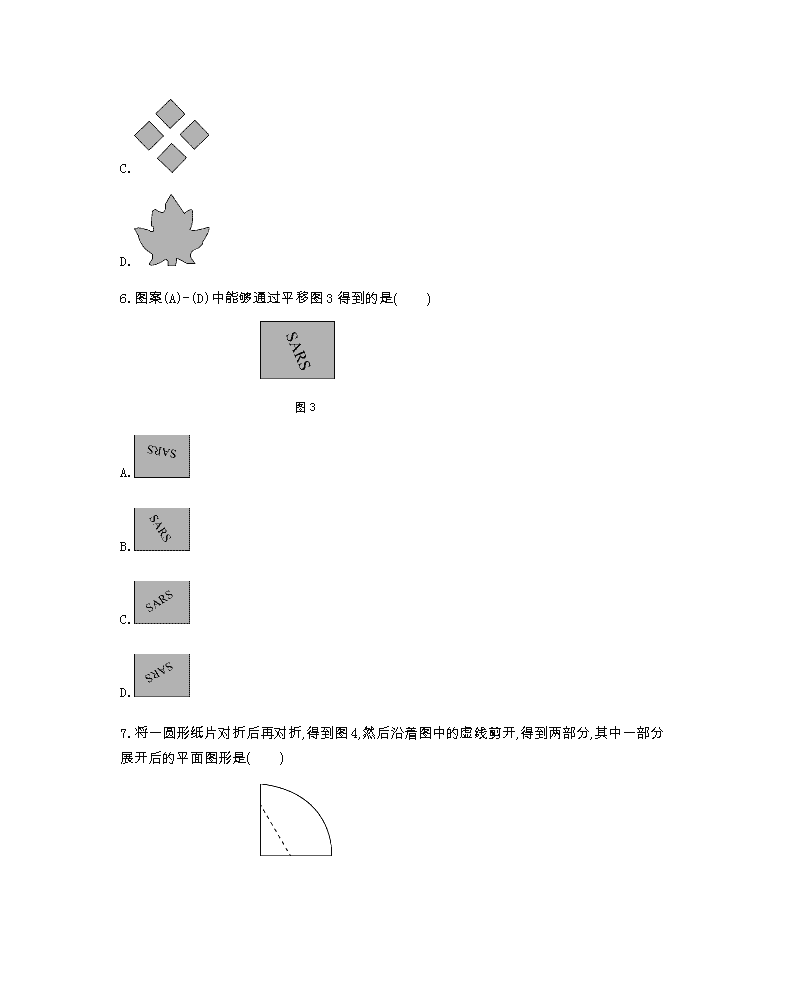
北师八下数学测试卷期末复习专项三 1.如图 1,将△ABC 绕点 A 旋转后得到△ADE,则旋转方式是( ) 图 1 A.顺时针旋转 90° B.逆时针旋转 90° C.顺时针旋转 45° D.逆时针旋转 45° 2.如图 2 是一个旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的 度数至少为( ) 图 2 A.30° B.45° C.60° D.90° 3.下列说法中不正确的是( ) A.中心对称是指两个图形的位置关系,必须涉及两个图形 B.中心对称图形是指一个具有特殊形状的图形,只对一个图形而言 C.如果把两个成中心对称的图形拼在一起,看成一个整体,那么它就是一个中心对称图形 D.中心对称就是中心对称图形的简称 4.下列图形中,是中心对称图形的是( ) A. B. C. D. 5.在下列图形中,是中心对称图形的是( ) A. B. C. D. 6.图案(A)-(D)中能够通过平移图 3 得到的是( ) 图 3 A. B. C. D. 7.将一圆形纸片对折后再对折,得到图 4,然后沿着图中的虚线剪开,得到两部分,其中一部分 展开后的平面图形是( ) 图 4 A. B. C. D. 8.如图 5,△ABC 和△ADE 均为正三角形,则图中可看作是旋转关系的三角形是( ) 图 5 A.△ABC 和△ADE B.△ABC 和△ABD C.△ABD 和△ACE D.△ACE 和△ADE 9.经过旋转,对应点到旋转中心的距离 . 10.线段是轴对称图形,它的对称轴是 ,线段也是中心对称图形,它的 对称中心是 . 11.从一副扑克牌中抽出梅花 2~10 共 9 张扑克牌,其中是中心对称图形的共有 张. 12.如图 6,△ABC 和△DEF 中,一个三角形经过平移可得到另一个三角形,则下列说法中不正 确的序号是 . 图 6 ①AB∥FD,AB=FD; ②∠ACB=∠FED; ③BD=CE; ④平移距离为线段 CD 的长度. 13.钟表的分针匀速旋转一周需要 60 分,它的旋转中心是 ,经过 25 分,分 针旋转 度. 14.如图 7,把大小相等的两个长方形拼成 L 形图案,则∠FCA= 度. 图 7 15.如图 8,线段 AB 的端点 A 移动到了点 D,你能作出线段 AB 平移后的图形吗? 图 8 16.如图 9 所示,在边长为 1 的网格中作出△ABC 绕点 A 按逆时针方向旋转 90°后的图形△ A1B1C1. 图 9 17.如图 10 所示,是跷跷板图,AO 和 BO 等长,横板 AB 通过点 O,且可以绕 O 点上下转动,如果 ∠OCA=90°,∠CAO= 25° ,问小孩玩跷跷板时上下最多可以转动多少度? 图 10 18.如图 11,△ABC 是等边三角形,边长为 2 cm,点 D 为 BC 的中点,连接 AD.△AEB 是△ADC 绕 点 A 顺时针旋转 60°得到的,连接 CE. (1)求 AD 的长; (2)求 EC 的长. 图 11 19.如图 12 所示,已知 MN⊥PQ , 垂足为 O ,点 A 、 A1 是以 MN 为轴的对称点,而点 A 、 A2 是以 PQ 为轴的对称点,则点 A1、A2 关于点 O 成中心对称,你能说明其中的道理吗? 图 12 20.已知△ABC 中,∠ACB=90°,∠A=30°,AB=2,BC=1,将△ABC 沿水平线(AB 所在的直线)作翻 转运动. 图 13 是△ABC 二次翻转形成的图形. (1)第一次翻转后的图形△BC’A’是由△ABC 按顺时针方向旋转所得的,那么哪一点是旋转中 心?旋转了多少度? (2)在下图中,画出△ABC 第三次翻转后的图形,请你仔细观察图中的△ABC 与由它第三次翻 转后的图形,想一想它们之间还可以是怎样的变换,请将它完整地表达出来. 图 13 参考答案 1.B 2.C 3.D 4.A 5.C 6.B 7.C 8.C 9.相等 10.线段的垂直平分线 线段的中点 11.3 12.④ 13.钟表的中心 150 14.45 15.略 16.略 17. 解：∠BOC=90°+25°=115°,B 点着地时,OB 与 OC 夹角为 65°. 跷跷板上下转动的角度为 115°-65°=50°. 18. 解：(1)BD=CD=1 cm, AD= 2 2-AC CD = 2 22 -1 = 3 (cm). (2) ∵△AEB 是△ADC 绕点 A 旋转 60°得到的, ∴AE=AD= 3 cm, ∠EAB=∠CAD=30°, ∠CAE=90°. CE= 2 2AE AC = 23 2 = 7 (cm). 19. 解：方法不唯一：如以 PQ 为 x 轴,MN 为 y 轴建立直角坐标系,设点 A 坐标为(a,b),则点 A1 坐标为(-a,b), 点 A2 坐标为(a,-b),可见：点 A1、A2 的横、纵坐标都互为相反数,两个点关于 O 点对称. 20. 解：(1)旋转中心是点 B,旋转了 120°; (2)图形： AC= 2 2-AB CB = 2 22 -1 = 3 , ∴BB”=1+ 3 +2=3+ 3 , ∴△A”B”C”是由△ABC 沿着 AB 所指的方向(即沿着水平线)向右平移了(3+ 3 )得到.