初中数学8年级教案：第12讲 特殊的平行四边形（下）

初中数学8年级教案：第12讲 特殊的平行四边形（下）

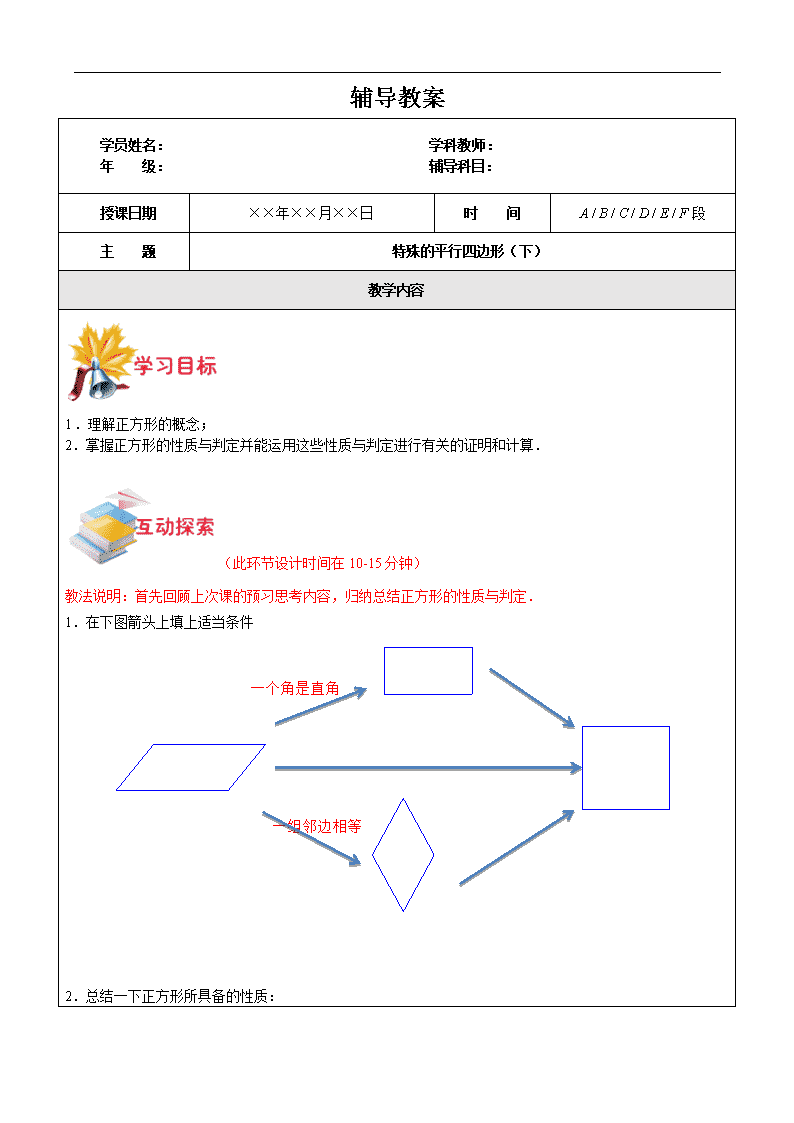
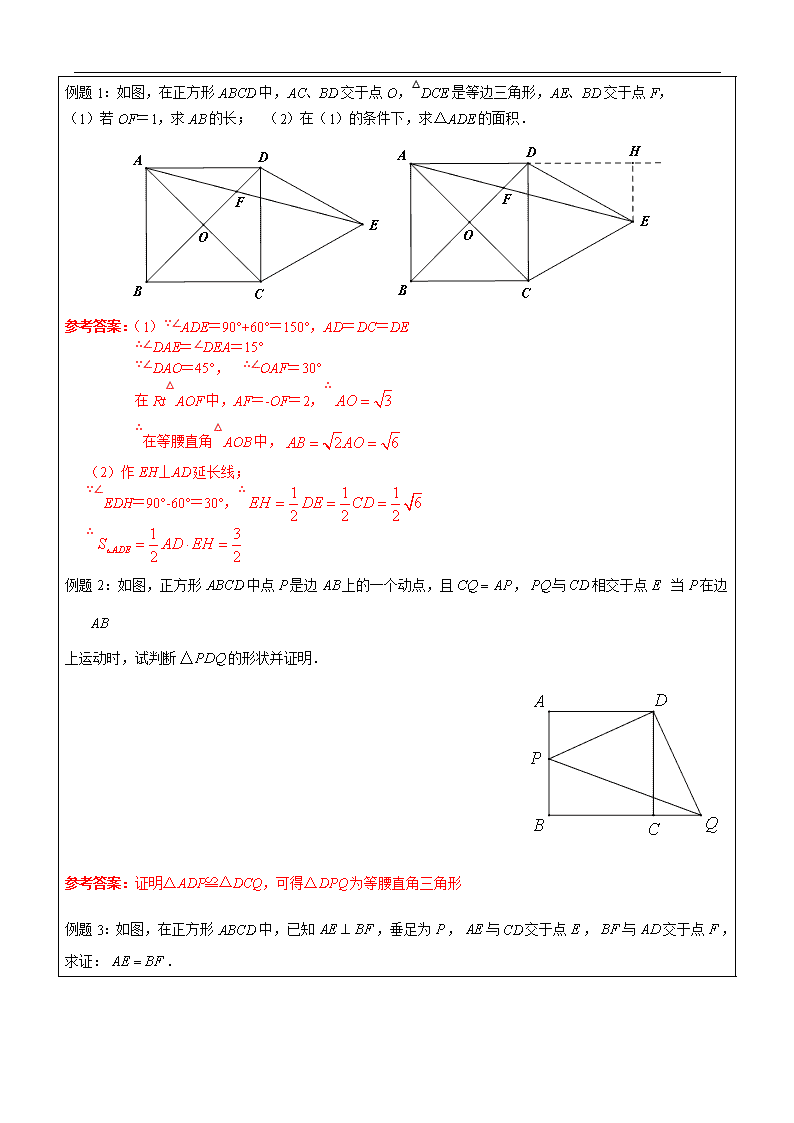
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目：‎ 授课日期 ‎××年××月××日 时 间 A / B / C / D / E / F段 主 题 特殊的平行四边形（下）‎ 教学内容 ‎1．理解正方形的概念；‎ ‎2．掌握正方形的性质与判定并能运用这些性质与判定进行有关的证明和计算．‎ ‎（此环节设计时间在10-15分钟）‎ 教法说明：首先回顾上次课的预习思考内容，归纳总结正方形的性质与判定．‎ ‎1．在下图箭头上填上适当条件 一组邻边相等 一个角是直角 ‎2．总结一下正方形所具备的性质：‎ 边 角 对角线 对称性 正方形 两组对边平行 四条边都相等 四个角都是直角 对角线互相垂直平分且相等 每一条对角线平分一组对角 中心对称 轴对称 ‎1．矩形、菱形、正方形都具有的性质是（ ）‎ A、对角线相等； B、对角线互相平分； C、对角线平分一组对角； D、对角线互相垂直 ‎2．下列判断中正确的是（　　）‎ A、四边相等的四边形是正方形 B、四角相等的四边形是正方形 C、对角线互相垂直的平行四边形是正方形 D、对角线互相垂直平分且相等的四边形是正方形 ‎3．已知四边形ABCD中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（ ）‎ A、∠D＝90°； B、AB＝CD； C、AD＝BC； D、BC＝CD.‎ ‎4．如图所示，已知在△ABC中，AB＝AC，AD是∠BAC的平分线，交BC于D，AN是△ABC外角∠CAM的平分线，CE⊥AN垂足为点E。 　‎ ‎（1）求证：四边形ADCE是矩形；‎ ‎（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？请加以证明．‎ 参考答案：1．B；2．D； 3．D； 4．当△ABC为等腰直角三角形时，四边形ADCE是一个正方形．‎ ‎（此环节设计时间在50-60分钟）‎ 例题1：如图，在正方形ABCD中，AC、BD交于点O，△DCE是等边三角形，AE、BD交于点F，‎ ‎（1）若OF＝1，求AB的长； （2）在（1）的条件下，求△ADE的面积．‎ 参考答案：（1）∵∠ADE＝90°+60°＝150°，AD＝DC＝DE ‎∴∠DAE＝∠DEA＝15°‎ ‎∵∠DAO＝45°， ∴∠OAF＝30° ‎ 在Rt△AOF中，AF＝-OF＝2，∴‎ ‎∴在等腰直角△AOB中，‎ ‎（2）作EH⊥AD延长线；‎ ‎∵∠EDH＝90°-60°＝30°，∴ ‎ ‎∴‎ 例题2：如图，正方形中点是边上的一个动点，且，与相交于点 当在边 上运动时，试判断的形状并证明．‎ 参考答案：证明△ADP≌△DCQ，可得△DPQ为等腰直角三角形 例题3：如图，在正方形中，已知，垂足为，与交于点，与交于点，‎ 求证：．‎ 参考答案：证明△ADP≌△DCQ，可得△DPQ为等腰直角三角形 例题4：如图，在正方形ABCD中，点O是对角线AC、BD的交点，作OE⊥OF，垂足为点O，OE、OF分别与边AB、BC交于点E、F，其中AE＝4，CF＝3，‎ ‎（1）求EF的长； （2）求△EOF的面积。‎ 参考答案：（1）∵四边形ABCD是正方形， ∴OB＝OC，∠BOC＝∠EOF＝90°， ∵OE⊥OF ∴∠BOC＝∠EOF＝90° ∴∠EOB＝∠FOC，‎ ‎∵∠ABC＝∠BCD＝90° ∴∠OCB＝∠OBE＝45°‎ 在△BOE和△COF中，∠OCB＝∠OBE＝45°，OB＝OC，∠EOB＝∠FOC， ∴△BOE≌△COF（ASA）∴BF＝AE＝4， 同理BE＝CF＝3 ∴在Rt△BEF中，EF＝5‎ ‎（2）∵△BOE≌△COF ∴OE＝OF ‎∴△OEF为等腰直角三角形 ∴OE＝OF＝‎ ‎∴‎ 例题5：如图所示，在△ABC中，点O在AC边上运动，过O作直线MN∥BC交∠BCA内角平分线于E点，外角平分线于F点．‎ ‎（1）求证：OE＝OF ‎（2）当点O运动到何处时，四边形AECF是矩形，请说明理由？‎ ‎（3）在第（2）问基础上，如果使四边形AECF变成正方形，需要在△ABC中添加什么条件，请说明理由？‎ ‎ ‎ 参考答案：‎ ‎（1）∵CE为∠BCA的平分线 ，∴∠BCE＝∠OCE 又∵MN∥BC，∴∠BCE＝∠OEC ‎∴∠OCE ＝∠OEC，∴OE＝OC 同理：OF＝OC ‎ ‎∴OE＝OF ‎（2） 当点O运动到AC中点时，四边形AECF是矩形；‎ 证明：∵AO＝CO，OE＝OF，∴四边形AECF是平行四边形， ∵∠ECA+∠ACF＝∠BCD，∴∠ECF＝90°， ∴四边形AECF是矩形 ‎（3）需添加∠ACB＝90°；‎ 证明：∵AC⊥BC，MN∥BC ‎∴AC⊥EF ‎∴四边形AECF是菱形 又∵四边形AECF是矩形 ‎∴四边形AECF是正方形 此环节设计时间在30分钟左右（20分钟练习＋10分钟互动讲解）。‎ ‎1．如图，是正方形的对角线上的一点，且，，、分别是垂足．‎ 求证：．‎ 参考答案：联结PC，证明PECF为矩形及△ADP≌△CDP即可 ‎ ‎2．如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．‎ ‎（1）求证：四边形ABCD是菱形；‎ ‎（2）若∠AED＝2∠EAD，求证：四边形ABCD是正方形．‎ 参考答案：（1）证明：∵四边形ABCD是平行四边形，∴AO＝CO． ‎ 又∵△ACE是等边三角形，∴EO⊥AC，即DB⊥AC． ‎ ‎∴平行四边形ABCD是菱形；‎ ‎（2）∵△ACE是等边三角形，∴∠AEC＝60°．‎ ‎∵EO⊥AC，∴∠AED＝30°．‎ ‎∵∠AED＝2∠EAD，∴∠EAD＝15°∴∠ADO＝∠EAD+∠AED ＝45°． ‎ ‎∵四边形ABCD是菱形，∴∠ADC＝2∠ADO＝90°． ‎ ‎∴四边形ABCD是正方形． ‎ ‎3．如图，正方形ABCD中，对角线的交点为O，E是 OC上的一点， AG⊥BE于 G，AG交 OB于 F，‎ 求证：OE＝OF．‎ 参考答案：∵四边形ABCD是正方形， ∴AC＝BD，OA＝OC，OB＝OD， ∴OA＝OB， ∵AC⊥BD，AG⊥BE， ∴∠FAO+∠AFO＝90°，∠EAG+∠AEG＝90°， ∴∠AFO＝∠BEO， 在△AOF和△BOE中，∠AFO＝∠BEO，∠FOA＝∠EOB，OA＝OB， ∴△AOF≌△BOE（AAS）， ∴OE＝OF；‎ 补充类试题：‎ ‎1．已知：如图所示：、分别是正方形的边、上的点，且，‎ 求证：．‎ 参考答案：辅助线如图所示，先证△ADF≌△ABG，再证△AEF≌△AEG即可 ‎（此环节设计时间在5-10分钟内）‎ 让学生回顾本节课所学的重点知识，以学生自我总结为主，学科教师引导为辅，为本次课做一个总结回顾 ‎【巩固练习】‎ ‎1．如图：正方形ABCD的边长为4，AE平分∠DAC，EF⊥AC，垂足为F，则FC＝ 。‎ ‎2．已知：如图，O为正方形ABCD对角线的交点，点E在边CB的延长线上，联结EO，OF⊥OE交BA延长线于点F，联结EF。‎ （1） 求证：EO＝FO；‎ （2） 若正方形的边长为2， OE＝2OA，求BE的长．‎ ‎3．如图，在正方形中，点、分别是边、的中点，与相交于，、的延长线相交于点，点是的中点.‎ 求证：（1） (2)‎ 参考答案：1．； ‎ ‎2．（1）证明：∵ABCD是正方形，对角线交于点O，‎ ‎∴AO＝BO，AC⊥BD，‎ ‎∴ ∠OAB＝∠OBA,∴∠OAF＝∠OBE，‎ ‎∵AC⊥BD，OF⊥OE，∴∠AOF＝＝∠BOE，‎ ‎∴△AOF≌△BOE，‎ ‎∴EO＝FO.‎ ‎（2）解：∵ABCD是正方形，边长为2，∴AO＝,∴OE＝2OA＝ ‎ ‎ ∵OF⊥OE，EO＝FO，∴EF＝4，‎ ‎ ∵△AOF≌△BOE，∴AF＝BE，‎ ‎ 设AF＝BE＝x， 在Rt△EFB中，,即 ‎ 解得，∵x＞0，∴，即BE＝‎ ‎3．证明：（1）∵正方形 ‎∴ ‎ ‎∵是的中点 ∴ ‎ ‎∵ ∴‎ ‎∴ ∴‎ ‎∵是的中点 ∴‎ ‎(2)证 ∴‎ ‎∵ ∴ ‎ ‎∵ ∴‎ ‎∴ ‎ ‎【预习思考】‎ ‎1．在箭头上填上适当的条件；‎ 一个角是直角，一组邻边相等 一组邻边相等 一个角是直角 四边形平行四边形平行四边形平行四边形平行四边形 梯形矩形矩形矩形矩形 直角梯形正方形正方形正方形正方形 等腰梯形菱形菱形菱形菱形 ‎2．回顾等腰梯形的性质与判定，完成下表：‎ 边 角 对角线 对称性 等腰梯形 等腰梯形的判定方法 边 角 对角线