- 2021-11-01 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册第2章特殊三角形2
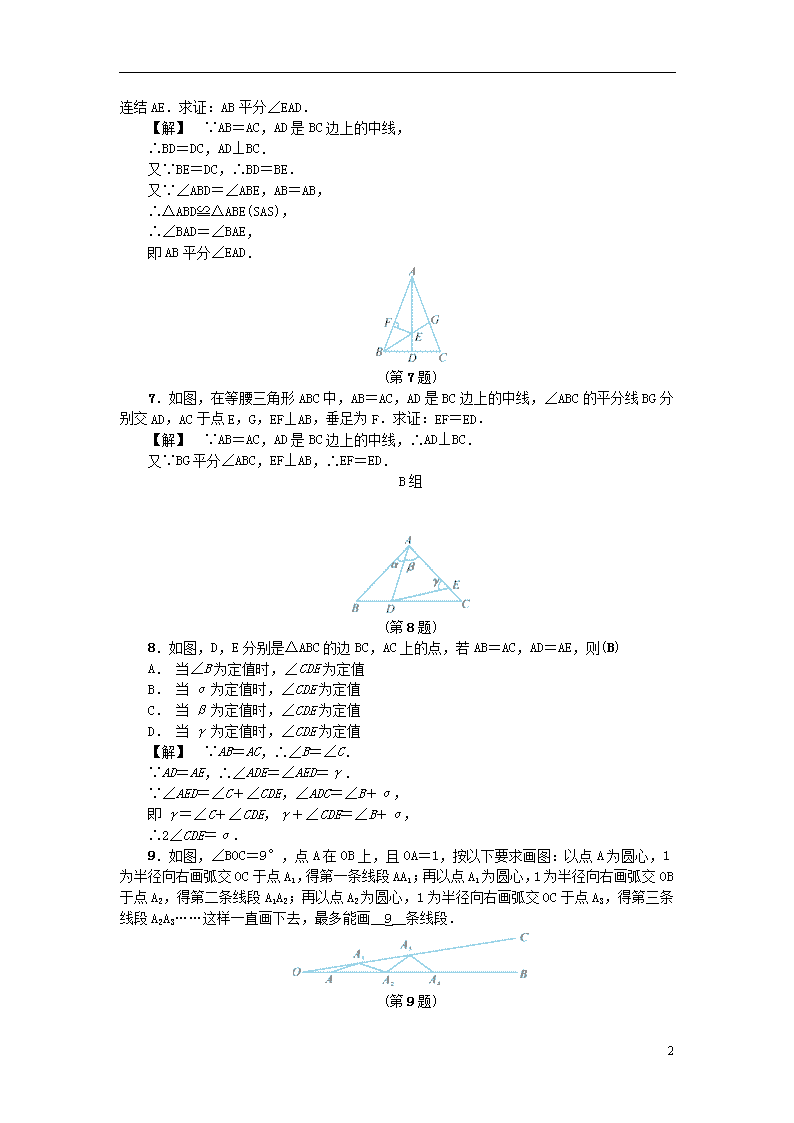
2.3 等腰三角形的性质定理(二) A组 1.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.若∠BAC=64°,则∠BAD的度数为__32°__. ,(第1题)) ,(第2题)) 2.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,已知BC=6,∠B=65°,则BD=__3__,∠ADB=__90°__,∠BAC=__50°__. 3.如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为(C) A. 35° B. 45° C. 55° D. 60° ,(第3题)) ,(第4题)) 4.如图,在△ABC中,AB=AC=6,AD⊥BC,垂足为D,CD=4,则△ABC的周长为(B) A. 18 B. 20 C. 22 D. 24 (第5题) 5.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,则DE=DF,请说明理由. 【解】 连结AD. ∵AB=AC,D为BC的中点, ∴∠BAD=∠CAD. ∵DE⊥AB,DF⊥AC,∴DE=DF. (第6题) 6.如图,在△ABC中,AB=AC,AD是BC边上的中线,作∠ABE=∠ABD,且BE=DC, 5 连结AE.求证:AB平分∠EAD. 【解】 ∵AB=AC,AD是BC边上的中线, ∴BD=DC,AD⊥BC. 又∵BE=DC,∴BD=BE. 又∵∠ABD=∠ABE,AB=AB, ∴△ABD≌△ABE(SAS), ∴∠BAD=∠BAE, 即AB平分∠EAD. (第7题) 7.如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG分别交AD,AC于点E,G,EF⊥AB,垂足为F.求证:EF=ED. 【解】 ∵AB=AC,AD是BC边上的中线,∴AD⊥BC. 又∵BG平分∠ABC,EF⊥AB,∴EF=ED. B组 (第8题) 8.如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则(B) A. 当∠B为定值时,∠CDE为定值 B. 当α为定值时,∠CDE为定值 C. 当β为定值时,∠CDE为定值 D. 当γ为定值时,∠CDE为定值 【解】 ∵AB=AC,∴∠B=∠C. ∵AD=AE,∴∠ADE=∠AED=γ. ∵∠AED=∠C+∠CDE,∠ADC=∠B+α, 即γ=∠C+∠CDE,γ+∠CDE=∠B+α, ∴2∠CDE=α. 9.如图,∠BOC=9°,点A在OB上,且OA=1,按以下要求画图:以点A为圆心,1为半径向右画弧交OC于点A1,得第一条线段AA1;再以点A1为圆心,1为半径向右画弧交OB于点A2,得第二条线段A1A2;再以点A2为圆心,1为半径向右画弧交OC于点A3,得第三条线段A2A3……这样一直画下去,最多能画__9__条线段. (第9题) 5 【解】 由题意可知:AO=A1A,A1A=A2A1,…, 则∠AOA1=∠OA1A,∠A1AA2=∠A1A2A,…. ∵∠BOC=9°,∴∠A1AB=2∠BOC=18°. 同理可得∠A2A1C=27°,∠A3A2B=36°,∠A4A3C=45°,∠A5A4B=54°,∠A6A5C=63°,∠A7A6B=72°,∠A8A7C=81°,∠A9A8B=90°, ∴第10个三角形将有两个底角等于90°,不符合三角形的内角和定理,故最多能画9条线段. 10.如图,在△ABC中,AB=AC,D是BC的中点,BF⊥AC于点F,交AD于点E,∠BAC=45°.求证:△AEF≌△BCF. (第10题) 【解】 过点F作FG⊥AB于点G. ∵∠BAC=45°,BF⊥AF, ∴∠ABF=45°. ∵FG⊥AB, ∴∠AGF=∠BGF=90°. 在△AGF和△BGF中, ∵ ∴△AGF≌△BGF(AAS), ∴AF=BF. ∵AB=AC,D是BC的中点, ∴AD⊥BC, ∴∠EAF+∠C=90°. ∵BF⊥AC, ∴∠AFE=∠BFC=90°,∠CBF+∠C=90°, ∴∠EAF=∠CBF. 在△AEF和△BCF中, ∵ ∴△AEF≌△BCF(ASA). (第11题) 5 11.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F. (1)求证:DE=DF. (2)问:如果DE,DF分别是∠ADB,∠ADC的平分线,那么它们还相等吗? 【解】 (1)∵AB=AC,AD⊥BC, ∴AD平分∠BAC. ∵DE⊥AB,DF⊥AC, ∴DE=DF. (2)相等.理由如下: 由(1)知AD⊥BC,∠DAE=∠DAF, ∴∠ADB=∠ADC=90°. ∵DE,DF分别是∠ADB,∠ADC的平分线, ∴∠ADE=∠ADB,∠ADF=∠ADC, ∴∠ADE=∠ADF. 在△ADE和△ADF中, ∵ ∴△ADE≌△ADF(ASA), ∴DE=DF. 数学乐园 (第12题) 12.如图,在等腰三角形ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线相交于点O,点C沿EF折叠后与点O重合,求∠CEF的度数. 【解】 连结BO. ∵∠BAC=50°,∠BAC的平分线与AB的中垂线相交于点O, ∴∠OBA=∠OAB=∠BAC=25°. ∵AB=AC,∠BAC=50°, ∴∠ABC=∠ACB=65°. ∴∠OBC=65°-25°=40°. 根据等腰三角形的对称性,得∠OCB=∠OBC=40°. ∵点C沿EF折叠后与点O重合, ∴EO=EC,∠CEF=∠OEF, ∴∠EOC=∠ECO=40°, 5 ∴∠CEF=∠OEF==50°. 5查看更多