八年级下册数学同步练习1-1 第1课时 三角形的全等和等腰三角形的性质 北师大版

八年级下册数学同步练习1-1 第1课时 三角形的全等和等腰三角形的性质 北师大版

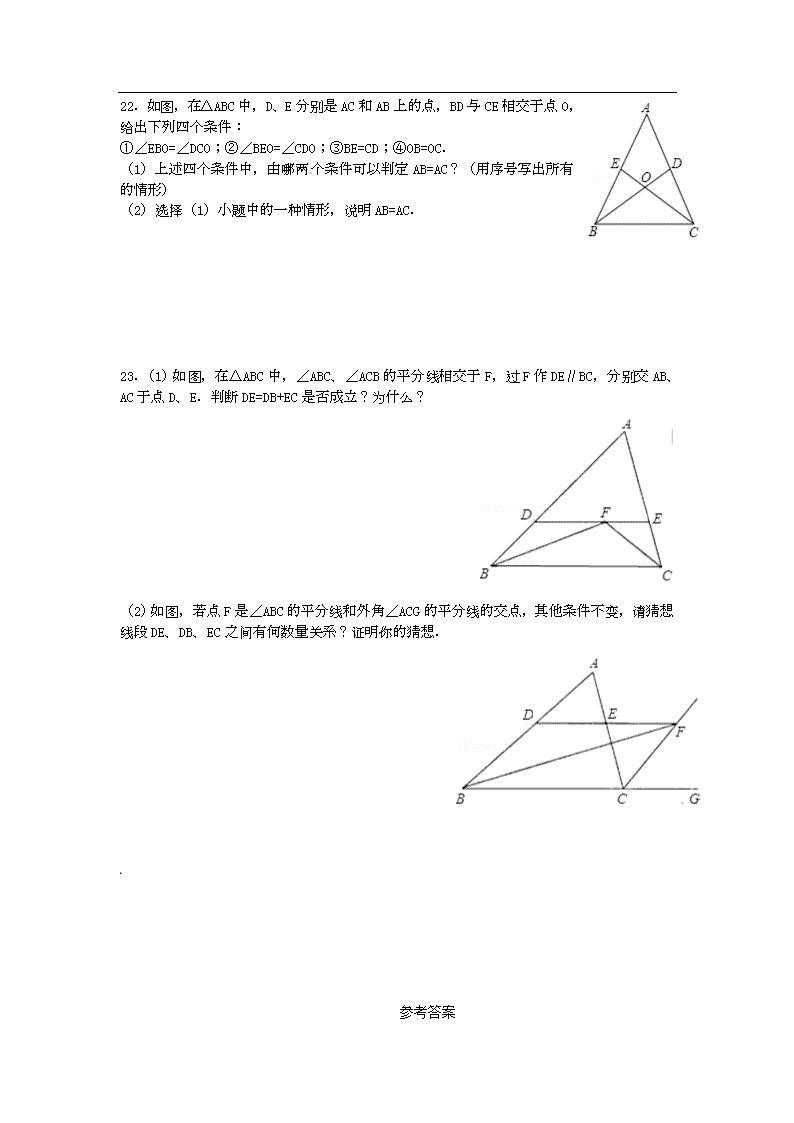
‎1.1 等腰三角形 第1课时 三角形的全等和等腰三角形的性质 一．选择题（共8小题）‎ ‎1．如图，在△ABC中，AB=AC，点D、E在BC上，连接AD、AE，如果只添加一个条件使∠DAB=∠EAC，则添加的条件不能为（　　）‎ A． BD=CE B． AD=AE C． DA=DE D． BE=CD　‎ ‎2．等腰三角形的一个角是80°，则它顶角的度数是（　　）‎ ‎　A． 80° B． 80°或20° C． 80°或50° D． 20°[来源:学+科+网Z+X+X+K]‎ ‎3．已知实数x，y满足，则以x，y的值为两边长的等腰三角形的周长是（　　）‎ A． 20或16 B． 20 C． 16 D． 以上答案均不对　‎ 4． 如图，在△ABC中，AB=AC，∠A=40°，‎ BD为∠ABC的平分线，则∠BDC的度数是（　　）‎ A． 60° B． 70° C． 75° D． 80°　‎ ‎5．已知等腰三角形的两边长分别是3和5，则该三角形的周长是（　　）‎ A． 8 B． 9 C． 10或12 D． 11或13‎ ‎6.如图，给出下列四组条件：‎ ‎①；②；‎ ‎③；④．‎ 其中，能使的条件共有（ ）‎ A．1组 B．2组 C．3组 D．4组 7． 在等腰△ABC中，AB=AC，中线BD将这个三角形的周长分为15和12两个部分，‎ 则这个等腰三角形的底边长为（　　）‎ A． 7 B． 11 C． 7或11 D． 7或10‎ ‎8．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（　　）‎ A． 60° B． 120° C． 60°或150° D． 60°或120°‎ 二．填空题（共10小题）　‎ ‎9．已知等腰三角形的一个内角为80°，则另两个角的度数是　_________　．　‎ ‎10．如图，已知AB∥CD，AB=AC，∠ABC=68°，则∠ACD=　_________　．‎ ‎　‎ 第10题 第11题 第12题 第13题 ‎11．如图，在△ABC中，AB=AC，△ABC的外角∠DAC=130°，则∠B=　_________　°．‎ ‎12．如图，AB∥CD，AE=AF，CE交AB于点F，∠C=110°，则∠A=________°．‎ ‎13．如图，在△ABC中，AB=AC，BC=6，AD⊥BC于D，则BD=_________　．　‎ ‎14．如图，在△ABC中，AB=AD=DC，∠BAD=32°，则∠BAC=_________　°．[来源:学科网]‎ ‎ ‎ 第14题 第15题 第16题 第17题 第18题 ‎15.如图，AB与CD交于点O，OA＝OC，OD＝OB，∠A=50°，∠B＝30°，则∠D的度数为_____.‎ ‎16．如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为　_________．‎ ‎17．如图，在△ABC中，AB=AC，点D为BC边的中点，∠BAD=20°，则∠C=　_________　．‎ ‎18．如图，在△ABC中，AB=AC，∠A=80°，E，F，P分别是AB，AC，BC边上一点，且BE=BP，CP=CF，则∠EPF=　_________　度．‎ 三．解答题（共5小题）‎ ‎19．已知：如图，在等腰△ABC中，AB=AC，O是底边BC上的中点，OD⊥AB于D，OE⊥AC于E．求证：AD=AE．‎ ‎20．如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．‎ 求证：（1）△ABD≌△ACD；‎ ‎（2）BE=CE．‎ ‎　‎ ‎21．如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，点E是AB的中点．试判断OE和AB的位置关系，并给出证明．‎ ‎　‎ ‎22．如图，在△ABC中，D、E分别是AC和AB上的点，BD与CE相交于点O，给出下列四个条件：‎ ‎①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD；④OB=OC．‎ ‎（1）上述四个条件中，由哪两个条件可以判定AB=AC？（用序号写出所有的情形）‎ ‎（2）选择（1）小题中的一种情形，说明AB=AC．‎ ‎　‎ ‎23．（1）如图，在△ABC中，∠ABC、∠ACB的平分线相交于F，过F作DE∥BC，分别交AB、AC于点D、E．判断DE=DB+EC是否成立？为什么？‎ ‎（2）如图，若点F是∠ABC的平分线和外角∠ACG的平分线的交点，其他条件不变，请猜想线段DE、DB、EC之间有何数量关系？证明你的猜想．‎ 参考答案 一、CBBCDCCD[来源:学*科*网Z*X*X*K]‎ 二、9、50°，50°或80°，20°；10、44；11、65；12、40；13、3；14、69；15、30°；‎ ‎16、72；17、70；18、50‎ 三、19、证明：∵AB=AC，‎ ‎∴∠B=∠C．‎ ‎∵OD⊥AB，OE⊥AC，‎ ‎∴∠ODB=∠OEC=90°．‎ ‎∵O是底边BC上的中点，‎ ‎∴OB=OC，‎ 在△OBD与△OCE中，‎ ‎∴△OBD≌△OCE（AAS）．‎ ‎∴BD=CE．‎ ‎∵AB=AC，‎ ‎∴AB﹣BD=AC﹣CE．‎ 即AD=AE．‎ ‎20、证明：（1）∵D是BC的中点，‎ ‎∴BD=CD，‎ 在△ABD和△ACD中，，‎ ‎∴△ABD≌△ACD（SSS）； …（4分）‎ ‎[来源:Zxxk.Com]‎ ‎（2）由（1）知△ABD≌△ACD，‎ ‎∴∠BAD=∠CAD，即∠BAE=∠CAE，‎ 在△ABE和△ACE中，‎ ‎∴△ABE≌△ACE （SAS），‎ ‎∴BE=CE（全等三角形的对应边相等）．‎ ‎（其他正确证法同样给分） …（4分）‎ ‎21、解：OE⊥AB．‎ 证明：在△BAC和△ABD中，，‎ ‎∴△BAC≌△ABD（SAS）．‎ ‎∴∠OBA=∠OAB，‎ ‎∴OA=OB．‎ 又∵AE=BE，∴OE⊥AB．‎ 答：OE⊥AB．‎ ‎22、（1）答：有①③、①④、②③、②④共4种情形．‎ ‎（2）解：选择①④，证明如下：‎ ‎∵OB=OC，‎ ‎∴∠OBC=∠OCB，‎ 又∵∠EBO=∠DCO，‎ ‎∴∠EBO+∠OBC=∠DCO+∠OCB，‎ 即∠ABC=∠ACB，‎ ‎∴AC=AB．‎ ‎②④‎ 理由是：在△BEO和△CDO中 ‎∵，‎ ‎∴△BEO≌△CDO，‎ ‎∴∠EBO=∠DCO，‎ ‎∵OB=OC，‎ ‎∴∠OBC=∠OCB，‎ ‎∴∠ABC=∠ACB，‎ ‎∴AB=AC，‎ ‎23、解：（1）成立；‎ ‎∵△ABC中BF、CF平分∠ABC、∠ACB，‎ ‎∴∠1=∠2，∠5=∠4．‎ ‎∵DE∥BC，∴∠2=∠3，∠4=∠6．‎ ‎∴∠1=∠3，∠6=∠5．‎ 根据在同一个三角形中，等角对等边的性质，可知：BD=DF，EF=CE．‎ ‎∴DE=DF+EF=BD+CE．‎ 故成立．‎ ‎（2）∵BF分∠ABC，‎ ‎∴∠DBF=∠FBC．[来源:学科网]‎ ‎∵DF∥BC，∴∠DFB=∠FBC．‎ ‎∴∠ABF=∠DFB，‎ ‎∴BD=DF．‎ ‎∵CF平分∠ACG，‎ ‎∴∠ACF=∠FCG．‎ ‎∵DF∥BC，‎ ‎∴∠DFC=∠FCG．‎ ‎∴∠ACF=∠DFC，‎ ‎∴CE=EF．‎ ‎∵EF+DE=DF，即DE+EC=BD．‎