数学华东师大版八年级上册课件11-1 平方根与立方根 第2课时

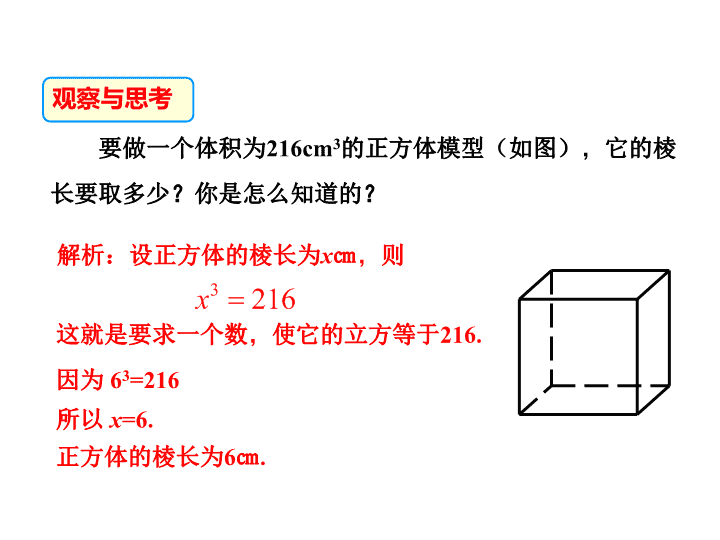
数学华东师大版八年级上册课件11-1 平方根与立方根 第2课时

第11章 数的平方 11.1 平方根与立方根 第2课时 学习目标 1.了解立方根和开立方的概念. 2. 会用根号表示一个数的立方根，掌握开立方运算. 3.会用计算器求一个数的立方根. 观察与思考 要做一个体积为216cm3的正方体模型（如图），它的棱 长要取多少？你是怎么知道的？ 解析：设正方体的棱长为x㎝，则 这就是要求一个数，使它的立方等于216. 因为 63=216， 所以 x=6. 正方体的棱长为6㎝. 3 216x  思考： 如果问题中正方体的体积为5cm3，正方体的边长又该 是多少？ 1.如何表示一个数的立方根? 一个数a的立方根可以表示为: a 3根指数 被开方数 其中a是被开方数，3是根指数，3不能省略. 读作：三次根号 a， 认识立方根一 如果一个数的立方等于a，那么这个数就叫做a的 立方根，也叫做a的三次方根．记作　　. 定义： a ３ 如果正方体的体积为5cm3，正方体的边长又该是多少？ 解：设正方体的边长为x，则 3 5x  所以正方体的边长是 3 5 ㎝. 想一想 求一个数的立方根的运算，叫做开立方. 立方 开立方 互逆 到现在我们学了几种运算? +，-，×，÷，乘方，开方（开平方，开立方） 根据立方根的意义填空. 因为23=8，所以8的立方根是(　) 因为( )3=0.125，所以0.125的立方是(　) 因为( )3＝－8，所以－8的立方根是( ) 因为( )3＝ ，所以 的立方( ) 8 27  8 27  2 -2 因为( )3＝0，所以0的立方根是(　)00 -2 通过这些题目的解答，你能看出正数、 0、负数的立方根各有什么特点? 1 2 2 1 3 2  3 2  请你自己也编三道求立方根的题目，并给出答案. 想一想 立方根的性质二 正数有立方根吗？如果有，有几个?负数呢？零呢？ 一个正数有一个正的立方根； 一个负数有一个负的立方根； 零的立方根是零. 立方根的特征 归纳总结 被开方数 平方根 立方根 有两个互为相反数 有一个，是正数 无平方根 零 有一个，是负数 零 正数 负数 零 讨论：你能归纳出平方根和立方根的异同点吗? 立方根是它本身的数有那些? 有1， -1， 0 平方根是它本身的数呢? 只有0 想一想 引伸探究： 因为 = 3 8 ， 3 8 = 3 8 3 8所以 3 2 73 2 7因为 = ， = 3 2 7 3 2 7所以 猜一猜： 你能从上述问题中总结出互为相反数的两个数a与-a的立 方根的关系吗？ = -2 -2 = -3-3 互为相反数的两 个数的立方根也 互为相反数 33 aa  3 32 3 3)2( 3 3)3( 3 34 3 30 规律：对于任何数a都有 2 -2 -3 4 0 例1 计算： aa 3 3 典例精析    33 8 33( 8)     33 27    33 27    33 0 规律：对于任何数a都有 8 -8 27 -27 0 aa 33 ）（ 说明：用计算器求一个有理数的立方根，只需直接按书写 顺序按键即可. 例2 用计算器求下列各数的立方根： （1）1331 ； （2）9.263（精确到0.01）． 探究用计算器求立方根 解：(1）在计算器上依次键入： 显示结果为11,所以 1 3 3 1 3 1331 11. SHIFT = （2）在计算器上依次键入： 显示结果为 2.1001511606987 ，要求精确到0.01，可得 9 . 2 6 3 = 3 9.263 2.10. SHIFT 1.判断下列说法是否正确，并说明理由. × （2） 25的平方根是5 × （3） -64没有立方根 × （4） -4的平方根是±2 × （5） 0的平方根和立方根都是0 √ （1） 8 27 的立方根是 2 3  当堂练习 2.求下列各式的值: 3 64 273 64（1） ； ； .（2） （3）3 125 解: 3 64（1） =4； 3 125（2） = 3 125 =-5； 273 64（3） 273 64= = .3 4 - 归纳: 求一个负数的立方根,可以先求出这个负数绝对值的立方 根,然后再取它的相反数. 立方根 立方根的概念、表 示及性质 用计算器求一个数 的立方根 课堂小结