上海教育版数学八上《反比例函数》同步练习

上海教育版数学八上《反比例函数》同步练习

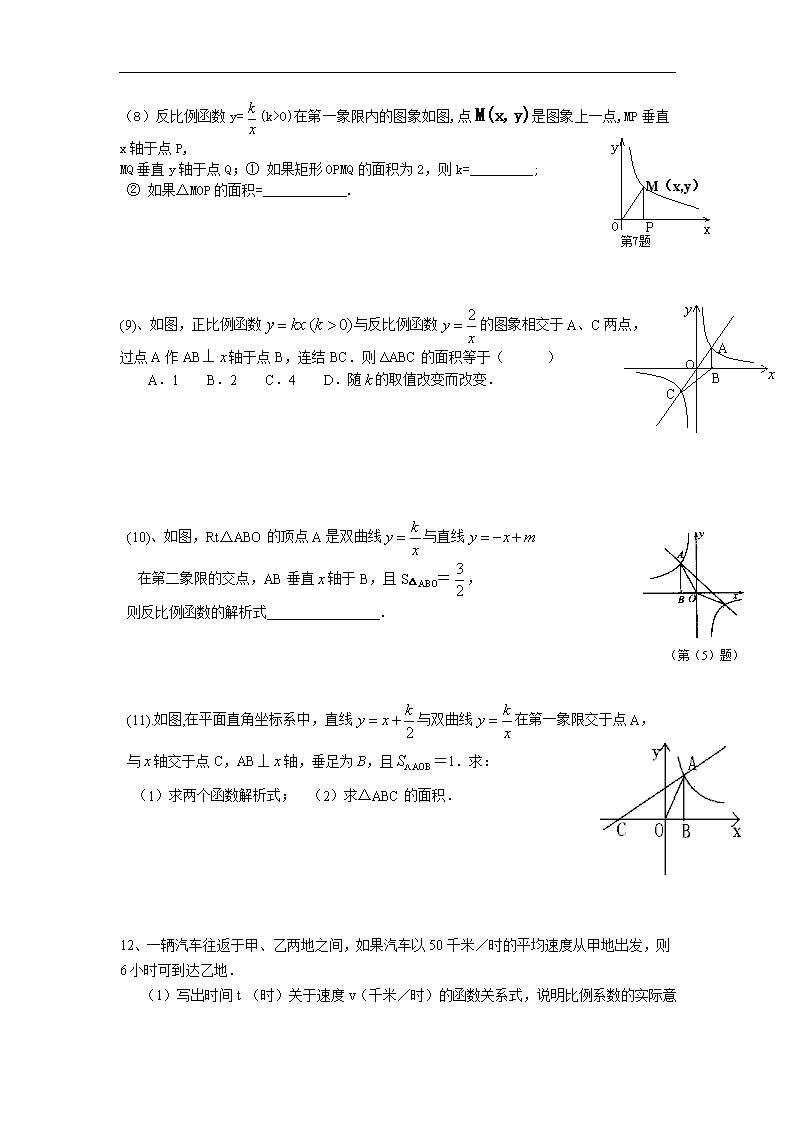
18.3 反比例函数 一、课本巩固练习 1、下列函数，① 1)2( yx ②. 1 1  xy ③ 2 1 xy  ④. xy 2 1 ⑤ 2 xy   ⑥ 1 3y x  ；其中是 y 关于 x 的反比例函数的有：_________________。 2、函数 22 )2(  axay 是反比例函数，则 a 的值是（ ） A．－1 B．－2 C．2 D．2 或－2 3、如果 y 是 m 的反比例函数， m 是 x 的反比例函数，那么 y 是 x 的（ ） A．反比例函数 B．正比例函数 C．一次函数 D．反比例或正比例函数 4、（1）如果 y 是 m 的正比例函数， m 是 x 的反比例函数，那么 y 是 x 的（ ） （2）如果 y 是 m 的正比例函数， m 是 x 的正比例函数，那么 y 是 x 的（ ） 5、反比例函数 ( 0ky kx   ）的图象经过（—2，5）和（ 2 ， n ）， 求（1） n 的值；（2）判断点 B（ 24 ， 2 ）是否在这个函数图象上，并说明理由 6、已知函数 1 2y y y  ，其中 1y 与 x 成正比例, 2y 与 x 成反比例，且当 x ＝1 时， y ＝1； x ＝3 时， y ＝5．求：（1）求 y 关于 x 的函数解析式； （2）当 x ＝2 时， y 的值． 7、写出一个反比例函数，使它的图象经过第二、四象限 ． 8、若反比例函数 22 )12(  mxmy 的图象在第二、四象限，则 m 的值是（ ） A、 －1 或 1; B、小于 1 2 的任意实数; C、－1; Ｄ、不能确定 9、已知 0k  ，函数 y kx k  和函数 ky x  在同一坐标系内的图象大致是（ ） 10、正比例函数 2 xy  和反比例函数 2y x  的图象有 个交点． 11、正比例函数 5y x  的图象与反比例函数 ( 0)ky kx   的图象相交于点 A（1， a ）， x y O x y O x y O x y O A B C D 则 a ＝ ． 二、基础过关 （1）下列函数中，当 0x  时， y 随 x 的增大而增大的是（ ） A． 3 4y x   B． 1 23y x   C． 4y x   D． 1 2y x  ． （2）已知反比例函数 2y x  的图象上有两点 A（ 1x ， 1y ），B（ 2x ， 2y ），且 1 2x x ， 则 1 2y y 的值是（ ） A．正数 B．负数 C．非正数 D．不能确定 （3）若点（ 1x ， 1y ）、（ 2x ， 2y ）和（ 3x ， 3y ）分别在反比例函数 2y x   的图象上， 且 1 2 30x x x   ，则下列判断中正确的是（ ） A． 1 2 3y y y  B． 3 1 2y y y  C． 2 3 1y y y  D． 3 2 1y y y  （4）在反比例函数 x ky 1 的图象上有两点 1 1( )x y， 和 2 2( )x y， ， 若 x x1 20  时， y y1 2 ，则 k 的取值范围是 ． （5）正比例函数 y=k1x(k1≠0)和反比例函数 y= 2k x (k2≠0)的一个交点为(m,n),则另一个交 点为______ ___. （6）老师给出一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质: 甲:函数的图象经过第二象限; 乙:函数的图象经过第四象限; 丙:在每个象限内,y随x的增 大而增大. 请你根据他们的叙述构造满足上述性质的一个函数: . （7）矩形的面积为 6cm2，那么它的长 y （cm）与宽 x （cm）之间的函数关系用图象表示为 （ ） （8）反比例函数 y= k x (k>0)在第一象限内的图象如图,点 M(x,y)是图象上一点,MP 垂直 x 轴于点 P, MQ 垂直 y 轴于点 Q；① 如果矩形 OPMQ 的面积为 2，则 k=_________; ② 如果△MOP 的面积=____________. o y x y xo y xo y xo A B C D P M（x,y） O y x 第7题 (9)、如图，正比例函数 ( 0)y kx k  与反比例函数 2y x  的图象相交于 A、C 两点， 过点 A 作 AB⊥ x 轴于点 B，连结 BC．则ΔABC 的面积等于（ ） A．1 B．2 C．4 D．随 k 的取值改变而改变． (10)、如图，RtΔABO 的顶点 A 是双曲线 ky x  与直线 y x m   在第二象限的交点，AB 垂直 x 轴于 B，且 S△ABO＝ 3 2 ， 则反比例函数的解析式 ． (11).如图,在平面直角坐标系中，直线 2 ky x  与双曲线 ky x  在第一象限交于点 A， 与 x 轴交于点 C，AB⊥ x 轴，垂足为 B，且 AOBS ＝1．求： （1）求两个函数解析式； （2）求△ABC 的面积． 12、一辆汽车往返于甲、乙两地之间，如果汽车以 50 千米／时的平均速度从甲地出发，则 6 小时可到达乙地． （1）写出时间 t （时）关于速度 v（千米／时）的函数关系式，说明比例系数的实际意 义． （2）因故这辆汽车需在 5 小时内从甲地到乙地，则此时汽车的平均速度至少应是多少？ y xO A C B （第（5）题） 13、你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：拉面师傅在一定体积的面 团的条件下制做拉面，通过一次又一次地拉长面条，测出每一次拉长面条后面条的总长度与 面条的粗细(橫截面积) （1）请根据右表中的数据求出面条的总长度 y（m）与面条的粗细(橫截面积) s(mm2)函数 关系式； (2)求当面条粗 1.6mm2 时， 面条的总长度是多少？ 拉面的橫截面积 S(mm2) 面条的总长度 y（m） 200 0．8 160 1 120 1．3 80 2 40 4．1