- 2021-10-26 发布 |
- 37.5 KB |
- 32页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学下册第2章四边形2-7正方形课件(湘教版)
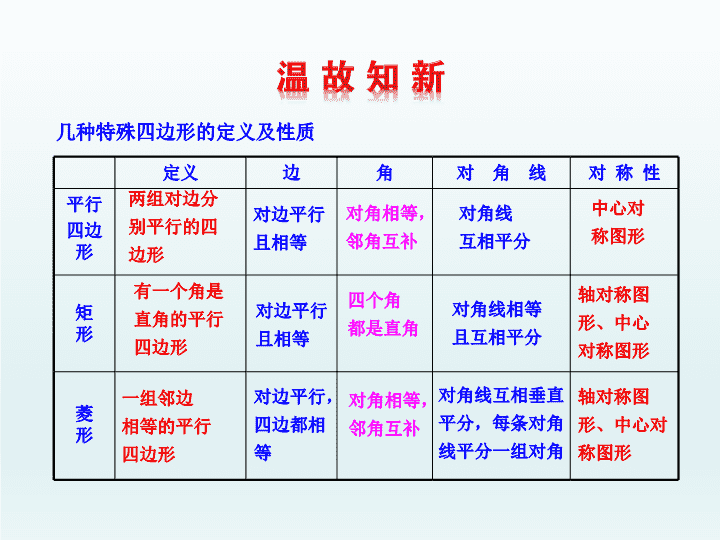
2.7 正方形 1. 掌握正方形的定义、性质和判定,并会用它们进行有关的证明和计算 . 2. 理解正方形与平行四边形、矩形、菱形的联系和区别 . 定义 边 角 对 角 线 对 称 性 平行 四边形 矩 形 菱 形 几种特殊四边形的定义及性质 对边平行 且相等 对边平行且相等 对边平行,四边都相等 对角相等, 邻角互补 四个角 都是直角 对角相等,邻角互补 对角线 互相平分 对角线相等 且互相平分 对角线互相垂直平分,每条对角线平分一组对角 中心对 称图形 轴对称图形、中心对称图形 轴对称图 形、中心对称图形 两组对边分 别平行的四 边形 有一个角是 直角的平行 四边形 一组邻边 相等的平行 四边形 矩形 正方形 〃 〃 矩形怎样变化后就成了正方形呢 ? 探究(一) 菱 形 ∟ ∟ ∟ ∟ 正方形 菱形怎样才能变形为正方形呢 ? 探究(二) 矩 形 〃 〃 正方形 邻边 相等 〃 〃 发现: 一组邻边相等的矩形是正方形 菱 形 一个角 是直角 正方形 ∟ 发现: 一个角为直角的菱形是正方形 正方形的定义 有一组邻边相等并且有一个角是直角的平行四边形叫作正方形 正方形性质 边 角 对角线 对称性 图形语言 文 字语言 符号语言 A C D B A C D B A C D B ∟ ∟ ∟ ∟ O ∟ 对边平行, 四条边都相等 四 个 角 都是直角 对角线互相垂直平分且相等,每条对角线平分一组对角 因为四边形 ABCD 是正方形 所以 AB∥CD AD∥BC, AB=BC=CD=AD 因为四边形 ABCD 是正方形 所以∠ A=∠B=∠C =∠D=90° 因为四边形 ABCD 是正方 形,所以 AC⊥BD,AC= BD,OA=OB=OC=OD, ∠1= ∠2= ∠3= ∠4= ∠5= ∠6= ∠7= ∠8 轴对称图形 中心对称图形 1 2 3 4 5 6 7 8 正方形是轴对称图形,它的对称轴是什么? 【 跟踪训练 】 根据图形所具有的性质 , 在下表相应的空格中打”√” 平行四边形 矩形 菱形 正方形 对边平行且相等 四边都相等 四个角都是直角 对角线互相平分 对角线互相垂直 对角线相等 √ √ √ √ √ √ √ √ √ √ √ √ √ √ 正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。 √ √ 求证:△ ABO 、△ BCO 、△ CDO 、△ DAO 是全等的等腰直角三角形 . △DAO 都是等腰直角三角形,并且 △ ABO≌△BCO≌△CDO≌△DAO. A B C D O 例 1 已知:如图,四边形 ABCD 是正方形,对 角线 AC 、 BD 相交于点 O , 证明: 因为 四边形 ABCD 是正方形, 所以 AC=BD , AC⊥BD , A O=BO=CO=DO. 所以△ ABO 、△ BCO 、△ CDO 、 【 例题 】 例 2 : AC 为正方形 ABCD 的对角线, E 为 AC 上一点,且 AB=AE , EF⊥AC 交 BC 于 F ,求证: EC=EF=FB A B C D E F ┌ 证明: 因为 四边形 ABCD 是正方形 所以 ∠ B=90° ,∠ ACB=45° , 因为 ∠ AEF=∠B =90° , AB=AE , AF=AF , 所以 △ ABF≌△AEF ( HL ), 所以 BF=EF , 又 因为 ∠ FEC=90° 所以 ∠ EFC=45° , 所以 EC=EF (等角对等边), 所以 BF=EF=EC . 【 例题 】 ( 红河 · 中考)如图,在正方形 ABCD 中, G 是 BC 上的任意一点( G 与 B 、 C 两点不重合), E 、 F 是 AG 上的两点( E 、 F 与 A 、 G 两点不重合),若 AF=BF+EF ,∠ 1=∠2 , 请判断线段 DE 与 BF 有怎样的位置关系,并证明你的结论 . 【 跟踪训练 】 【 解析 】 根据题目条件可判断 DE∥BF. 证明如下: 因为 四边形 ABCD 是正方形, 所以 AB=AD , 因为 AF=AE+EF ,又 AF=BF+EF, 所以 AE=BF, 因为 ∠ 1=∠2 ,所以△ ABF≌△DAE ( SAS ) . 所 以∠ AFB=∠DEA ,∠ BAF=∠ADE. 因为∠ BAF+∠2=90°, 所以 ∠ ADE+∠2=90° ,所以 ∠ BAF+ ∠1=90° 所以 ∠ AED=∠BFA=90°, 所以 DE∥BF. 一组邻边相等 有一个内角是直角 一组邻边相等 有一个内角是直角 正方形的判定 一组邻边相等且 有一个角是直角 A B C D E F G H 1 2 3 例 3 已知 : 正方形 ABCD 中 , 点 E , F , G , H 分别在 AB , BC , CD , DA 上 , 且 AE=BF=CG=DH, 试判断四边形 EFGH 是正方形吗 ? 并证明你的结论 . 【 例题 】 证明: 四边形 EFGH 是正方形, 因为四 边形 ABCD 是正方形, 所以 ∠ ABC=∠BCD=∠CDA=∠DAB=90° , AB=AD=DC=BC . 又 因为 AE=BF=CG=DH , 所以 AB-AE=AD-DH=DC-CG=BC-BF , 即 BE=AH=DG=CF , 所以 △ AEH≌△BFE≌ △CGF ≌ △DHG .所以 EH=HG=FG=EF , 因为 ∠ 1=∠3 .又∠ 3+∠2=90° 所以∠ 1+∠2=90° . 所以 四边形 EFGH 是正方形. 1.ABCD 是一块正方形场地,小华和小芳在 AB 边上取定了一点 E ,经测 EC=50m , EB=30m ,这块场地的面积和对角线长分别是多少? A D B C E 【 解析 】 连接 AC. 因为 四边形 ABCD 是正方形 所以 ∠ B=90° , AB=BC 因为 EC=50m , EB=30m 所以 S 正方形 ABCD =(4 0 m ) 2 =1600(m 2 ) 所以 所以 【 跟踪训练 】 2. 在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分 ( 不考虑道路的宽度 ). 你有几种方法? 解析: 有无数方法,只要两直线垂直且交点在正方形的对角线交点处即可 . 平行四边形 矩形 菱形 正 方 形 3. 你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗? 解析: 1. ( 义乌 · 中考)下列说法不正确的是 ( ) ( A )一组 邻 边相等的矩形是正方形 ( B )对角线相等的菱形是正方形 ( C )对角线互相垂直的矩形是正方形 ( D )有一个角是直角的平行四边形是正方形 【 解析 】 选 D. 有一个角是直角的平行四边形可能是 矩形,也可能是正方形 . 2. (苏州 · 中考)如图,四边形 ABCD 是正方形,延长 AB 到 E ,使 AE=AC , 则∠ BCE 的度数是 _______°. 【 解析 】 因为 四边形 ABCD 是正方形, 所以 ∠ CAE=45 ° ,∠ ABC=90°, 又 因为 AE=AC, 所以 ∠ E=∠ACE=67.5°, 所以 ∠ BCE=90°- ∠ E=90°-67.5°=22.5°. 答案: 22.5 3. ( 宜宾 · 中考)如图,点 P 是正方形 ABCD 的对角线 BD 上一 点 , PE⊥BC 于点 E , PF⊥CD 于点 F ,连接 EF, 给出 下列五个结论:① AP=EF ;② AP⊥EF ;③△ APD 一定是等 腰三角形;④∠ PFE=∠BAP ;⑤ PD= EC. 其中正确结 论的序号是 _____. 【 解析 】 延长 FP 交 AB 于点 G ,延长 AP 交 EF 于点 H ,交 EC 于点 M ,由题意易证,△ BPE 、△ DPF 为等腰直角三角形,四边形 PECF 为矩形,四边形 BEPG 为正方形 . 易证△ APG≌△FEP, 所以 AP=EF ,∠ BAP=∠PFE ,又 PE∥FC, 所以 ∠ PFE=∠FEC=∠BAP, 又∠ BAP+∠BMA=90° ,所以 ∠ FEM+∠BMA=90° , 所以 ∠ EHM=90° 即 AP⊥EF. 在等腰直角三角形 PDF 中 , PD= PF= EC. 答案: ①②④⑤ 4. 如图,正方形 ABCD 和正方形 OEFG 的边 长均为 4 , O 是正方形 ABCD 的旋转对称中 心,则图中阴影部分的面积是 ______. 【 解析 】 连接 OC,OD. 易证图中阴影部分 的面积等于△ COD 的面积 , 即正方形面积 的四分之一 , 故阴影部分面积为 4. 答案: 4 5. ( 滨州 · 中考 ) 如图,四边形 ABCD 中, E 、 F 、 G 、 H 分别是 AB 、 BC 、 CD 、 DA 的中点, ( 1 )请判断四边形 EFGH 的形状?并说明为什么 . ( 2 )要使四边形 EFGH 为正方形,那么四边形 ABCD 的对角线应该有怎样的情况? 【 解析 】 ( 1 )四边形 EFGH 是平行四边形 . 连接 AC, 因为 E 、 F 分别是 AB 、 BC 的中点 所以 EF∥AC , EF= AC 同理 HG∥AC , HG= AC 所以 EF HG, 所以 四边形 EFGH 是平行四边形 . ( 2 )四边形 ABCD 的对角线互相垂直且相等 . 通过本课时的学习,需要我们 1. 掌握正方形的定义、性质、判定 . 2. 了解正方形、矩形、菱形、平 行 四边形间的关系,认识它们之间的联系和区别 . 3. 能综合利用正方形的性质与判定解决有关的证明与计算 . 一、正方形的定义: 直角 相等 平行且相等 相等 垂直平分 一组对角 中心 轴 4 菱形 矩形 矩形 菱形 相等 直角 天将降大任于斯人也,必先苦其心志,劳其筋 骨,饿其体肤,空乏其身,行拂乱其所为。 —— 《 孟子 • 告子下 》查看更多