八年级下册数学周周测第十八章 平行四边形周周测9（全章）人教版

八年级下册数学周周测第十八章 平行四边形周周测9（全章）人教版

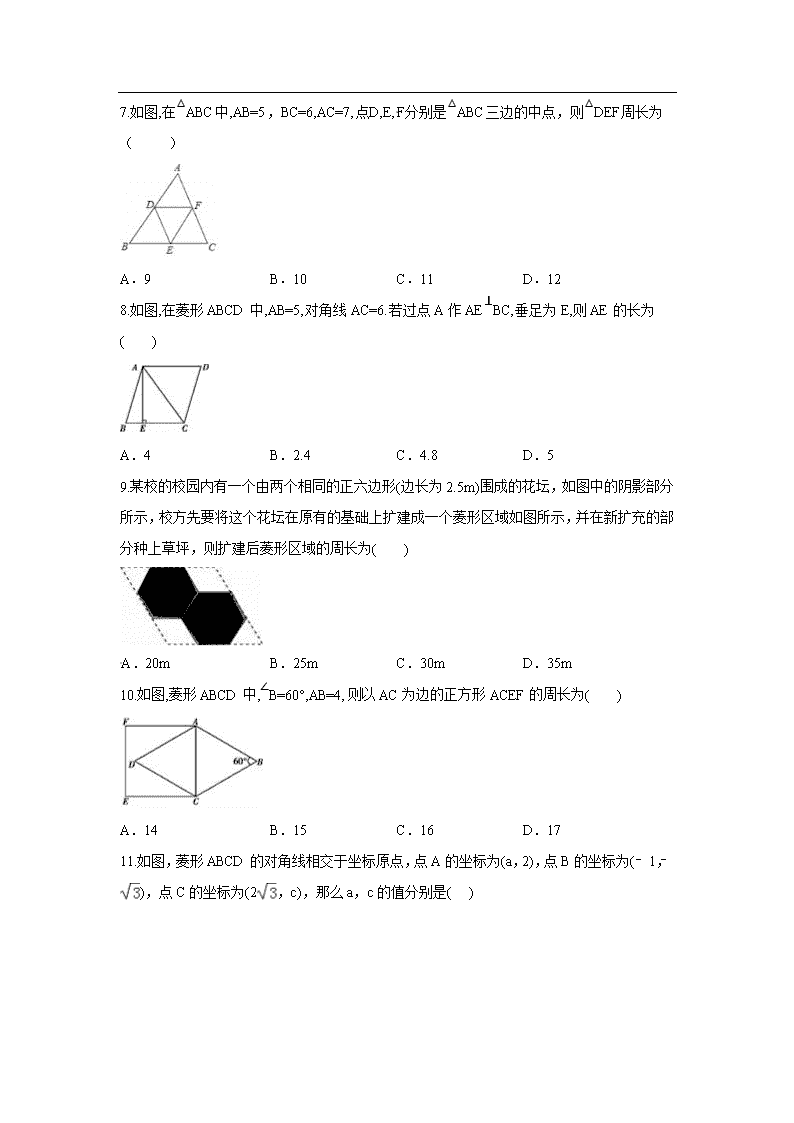
第十八章 平行四边形周周测9‎ 一 选择题 下列命题中,真命题是（ ）‎ A．对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形 C.对角线互相平分的四边形是平行四边形 D.对角线互相垂直平分的四边形是正方形 下列命题中，不正确的是（　　）‎ A．有一个角是60°的等腰三角形是等边三角形 B.一组对边平行且一组对角相等的四边形是平行四边形 C.对角线互相垂直且相等的四边形是矩形 D.对角线相等的菱形是正方形 已知▱ABCD的周长为32，AB=4，则BC=（　　） ‎ A．4 B．12 C．24 D．28 ‎ 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为（ ）‎ A．13 B．14 C．15 D．16‎ 如图,将▱ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=（ ）‎ A．2 B．3 C．4 D．5‎ 如图，在菱形ABCD中，BE⊥AD，BF⊥CD，E、F 为垂足，AE=ED ，则∠EBF等于( ) ‎ A．75° B．60° C．50° D．45° ‎ 如图,在△ABC中,AB=5，BC=6,AC=7,点D,E,F分别是△ABC三边的中点，则△DEF周长为（ ）[来源:Zxxk.Com]‎ A．9 B．10 C．11 D．12‎ 如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为(　　)‎ A．4 B．2.4 C．4.8 D．5‎ 某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛，如图中的阴影部分所示，校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示，并在新扩充的部分种上草坪，则扩建后菱形区域的周长为(　　)‎ A．20m B．25m C．30m D．35m 如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为(　　)‎ A．14 B．15 C．16 D．17‎ 如图，菱形ABCD的对角线相交于坐标原点，点A的坐标为(a，2)，点B的坐标为(﹣1，﹣)，点C的坐标为(2，c)，那么a，c的值分别是(     )‎ A．a=﹣1，c=﹣ B．a=﹣2，c=﹣2 C．a=1，c= D．a=2，c=2‎ 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，正确的有( )‎ A．1个 B．2个 C．3个 D．4个 二 填空题 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是________(写出一个即可).‎ 如图，在Rt△ABC中，∠ACB=90°，点D、E、F分别是AB、AC、BC中点，若CD=5，则EF长为    .‎ 如图,在矩形ABCD中,AB=3cm，BC=4cm，点E是BC边上的一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE长为________．‎ 如图，菱形ABCD中，AB=4，∠B=60°，E，F分别是BC，DC上的点，∠EAF=60°，连接EF，则△AEF的面积最小值是　　 ．‎ 如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°，现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为______个. ‎ 如图，已知正方形ABCD的边长为10，点P是对角线BD上的一个动点，M、N分别是BC、CD边上的中点，则PM＋PN的最小值是___________．‎ 三 作图题 如图，将四边形ABCD放在每个小正方形的边长为1的网格中，点A．B、C、D均落在格点上．‎ ‎（Ⅰ）计算AD2+DC2+CB2的值等于 ；‎ ‎（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AD2+DC2+CB2，并简要说明画图方法（不要求证明）．‎ 四 解答题 如图，点E、F为线段BD的两个三等分点，四边形AECF是菱形．‎ ‎（1）试判断四边形ABCD的形状，并加以证明；‎ ‎（2）若菱形AECF的周长为20，BD为24，试求四边形ABCD的面积．‎ ‎ ‎ 如图，已知在▱ABCD中，E、F是对角线BD上的两点，且BF=DE．求证：AE=CF．‎ 如图，在△ABC中，AB=BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．求证：四边形BECD是矩形．‎ 如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF=CE．‎ ‎（1）求证：四边形ACEF是平行四边形；‎ ‎（2）当∠B满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．‎ 将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F，‎ ‎（1）求证：四边形AECF为菱形；‎ ‎（2）若AB=4，BC=8，求菱形的边长；‎ ‎（3）在（2）的条件下折痕EF的长．‎ ‎ ‎ 如图，已知平行四边形ABCD的两条对角线相交于点O，E是BO的中点，过B点作AC的平行线，交CE的延长线于点F，连接BF ‎（1）求证：FB=AO；‎ ‎（2）当平行四边形ABCD满足什么条件时，四边形AFBO是菱形？说明理由．‎ 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠‎ ACB的平分线于点E,交∠ACB的外角平分线于点F．‎ ‎（1）求证：OE=OF；‎ ‎（2）若CE=12,CF=5,求OC的长；‎ ‎（3）当点O在边AC上运动到什么位置时,四边形AECF是矩形？并说明理由．‎ ‎[来源:学|科|网Z|X|X|K]‎ 第十八章 平行四边形周周测9试题答案 C． B．B. A C； C C； B. C C. C.‎ C；B=BF或BE⊥CF或∠EBF=60°或BD=BF(答案不唯一)‎ 5 3或1.5 ． 3 10 ‎ 解：（1）∵AD2=32+12=10，DC2=32+12=10，CB2=12+12=2，‎ ‎∴AD2+DC2+CB2=10+10=2=22，故答案为：22；‎ ‎（2）如图，以AB为边做正方形ABGH，再作平行四边形HMNG，直线MN交AH于点Q，交GB于点P，矩形ABPQ即为所求．理由是：∵S▱HMNG=2×6﹣2×（+1+×5×1）=4，∴S矩形HQNG=S▱HMNG=4，‎ ‎∵S正方形ABGH=（）2=26，∴S矩形ABPQ=26﹣4=22，所以画出的矩形ABPQ的面积等于AD2+DC2+CB2．‎ 解：（1）四边形ABCD为菱形．理由如下：如图，连接AC交BD于点O，‎ ‎∵四边形AECF是菱形，∴AC⊥BD，AO=OC，EO=OF，‎ 又∵点E、F为线段BD的两个三等分点，∴BE=FD，∴BO=OD，‎ ‎∵AO=OC，∴四边形ABCD为平行四边形，∵AC⊥BD，∴四边形ABCD为菱形；‎ ‎（2）∵四边形AECF为菱形，且周长为20，∴AE=5，∵BD=24，∴EF=8，OE=EF=×8=4，‎ 由勾股定理得，AO===3，∴AC=2AO=2×3=6，‎ ‎∴S四边形ABCD=BD•AC=×24×6=72．‎ 证明：连接AC交BD于点O，连接AF、CE[来源:学科网]‎ ‎∵▱ABCD∴OA=OC，OB=OD ∵OF=BF﹣OB，OE=DE﹣OD,BF=DE∴OE=OF ‎∵OA=OC，OE=OF ∴四边形AECF是平行四边形∴AE=CF 证明：∵AB=BC，BD平分∠ABC，∴BD⊥AC，AD=CD．‎ ‎∵四边形ABED是平行四边形，∴BE∥AD，BE=AD，∴BE=CD，‎ ‎∴四边形BECD是平行四边形．∵BD⊥AC，∴∠BDC=90°，∴▱BECD是矩形．‎ 解：（1）∵ED是BC的垂直平分线∴EB=EC，ED⊥BC，∴∠3=∠4，‎ ‎∵∠ACB=90°，∴FE∥AC，∴∠1=∠5，‎ ‎∵∠2与∠4互余，∠1与∠3互余∴∠1=∠2，∴AE=CE，‎ 又∵AF=CE，∴△ACE和△EFA都是等腰三角形，∴∠5=∠F，∴∠2=∠F，‎ ‎∴在△EFA和△ACE中∵∠1=∠5,∠2=∠F,AF=CE，∴△EFA≌△ACE（AAS），‎ ‎∴∠AEC=∠EAF∴AF∥CE∴四边形ACEF是平行四边形；‎ ‎（2）当∠B=30°时，四边形ACEF是菱形．证明如下：‎ ‎∵∠B=30°，∠ACB=90°∴∠1=∠2=60°∴∠AEC=60°∴AC=EC ‎∴平行四边形ACEF是菱形．‎ 证明：（1）如图，取BC的中点G，连接EG．[来源:Zxxk.Com]‎ ‎∵E是BO的中点，∴EG是△BFC的中位线，∴EG=0.5BF．同理，EG=0.5OC，∴BF=OC．‎ 又∵点O是▱ABCD的对角线交点，∴AO=CO，∴BF=AO．‎ 又∵BF∥AC，即BF∥AO，∴四边形AOBF为平行四边形，∴FB=AO；‎ ‎（2）当平行四边形ABCD是矩形时，四边形AFBO是菱形．理由如下：‎ ‎∵平行四边形ABCD是矩形，∴OA=OB，∴平行四边形AFBO是菱形．‎ （1）证明：∵MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F，‎ ‎∴∠2=∠5，∠4=∠6，∵MN∥BC，∴∠1=∠5，∠3=∠6，‎ ‎∴∠1=∠2，∠3=∠4，∴EO=CO，FO=CO，∴OE=OF；‎ ‎（2）解：∵∠2=∠5，∠4=∠6，∴∠2+∠4=∠5+∠6=90°，‎ ‎∵CE=12，CF=5，∴EF==13，∴OC=EF=6.5；‎ ‎（3）解：当点O在边AC上运动到AC中点时，四边形AECF是矩形．‎ 证明：当O为AC的中点时，AO=CO，∵EO=FO，∴四边形AECF是平行四边形，‎ ‎∵∠ECF=90°，∴平行四边形AECF是矩形．‎ ‎[来源:学§科§网]‎