八年级下数学课件八年级下册数学课件《线段的垂直平分线》 北师大版 (5)_北师大版

八年级下数学课件八年级下册数学课件《线段的垂直平分线》 北师大版 (5)_北师大版

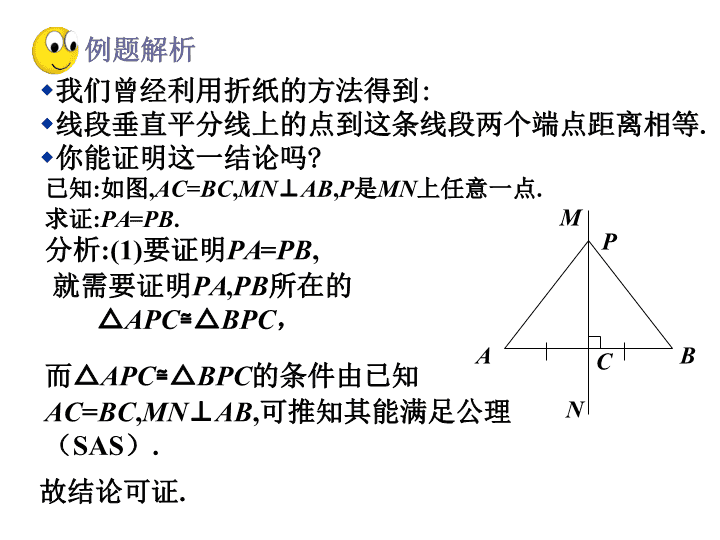
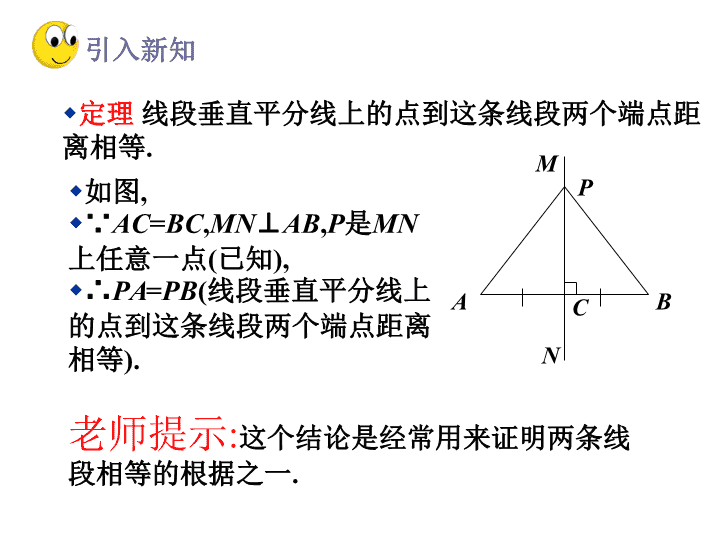
1.3线段的垂直平分线（1） 北师大课标九上·§1.3 (1) w我们曾经利用折纸的方法得到: w线段垂直平分线上的点到这条线段两个端点距离相等. w你能证明这一结论吗? 已知:如图,AC=BC,MN⊥AB,P是MN上任意一 点.求证:PA=PB. A C B P M N 分析:(1)要证明PA=PB, 而△APC≌ △BPC的条件由已知 故结论可证. AC=BC,MN⊥AB,可推知其能满足公理 （SAS）. 就需要证明PA,PB所在的 △APC≌ △BPC， 例题解析 w定理 线段垂直平分线上的点到这条线段两个端点 距离相等. 老师提示:这个结论是经常用来证明两条线 段相等的根据之一. A C B P M N w如图, w∵AC=BC,MN⊥AB,P是MN 上任意一点(已知), w∴PA=PB(线段垂直平分线上 的点到这条线段两个端点距离 相等). 引入新知 w你能写出“定理 线段垂直平分线上的点到这条 线段两个端点距离相等”的逆命题吗? w逆命题 到一条线段两个端点距离相等的点,在这条 线段的垂直平分线上. w它是真命题吗? A B P 如果是.请你证明它. 已知:如图,PA=PB. 求证:点P在AB的垂直平分线上. 分析:要证明点P在线段AB的垂直平分线上,可以先 作出过点P的AB的垂线(或AB的中点,),然后证明另 一个结论正确. 想一想:若作出∠P的角平分线,结论是否也可以得证? 想一想 w逆定理 到一条线段两个端点距离相等的点,在 这条线段的垂直平分线上. A C B P M N w如图, w∵PA=PB(已知), w∴点P在AB的垂直平分线上(到一 条线段两个端点距离相等的点,在这 条线段的垂直平分线上). 老师提示:这个结论是经常用来证 明点在直线上(或直线经过某一点)的 根据之一. 从这个结果出发,你还能联想到什么? 想一想 l已知:线段AB,如图. l求作:线段AB的垂直平分线. l作法: l用尺规作线段的垂直平分线. l1.分别以点A和B为圆心,以大于AB/2长 为半径作弧,两弧交于点C和D. A B C Dl2. 作直线CD. l则直线CD就是线段AB的垂直平分线. 请你说明CD为什么是AB的垂直平分线, 并与同伴进行交流. 老师提示:因为直线CD与线段AB的交点就是AB的中 点,所以我们也用这种方法作线段的中点. 想一想 l如图,已知AB是线段CD的垂直平分线,E是 AB上的一点,如果EC=7cm,那么ED= cm; 如果∠ECD=600,那么∠EDC= 0. 老师期望: 你能说出填空结果的根据. E D A B C 7 60 课堂练习 w 定理 w 线段垂直平分线上的点到这条线段 两个端点距离相等. 如图,∵AC=BC,MN⊥AB,P是MN上任 意一点(已知), ∴PA=PB(线段垂直平分线上的点到这 条线段两个端点距离相等). 逆定理 到一条线段两个端点距离相等 的点,在这条线段的垂直平分线上. 如图, ∵PA=PB(已知), ∴点P在AB的垂直平分线上(到一条线 段两个端点距离相等的点,在这条线 段的垂直平分线上). A C B P M N 课堂小结 独立 作业 习题1.7 祝你成功！