2017-2018学年安徽省安庆市岳西县冶溪中学七年级（上）期中数学试卷

2017-2018学年安徽省安庆市岳西县冶溪中学七年级（上）期中数学试卷

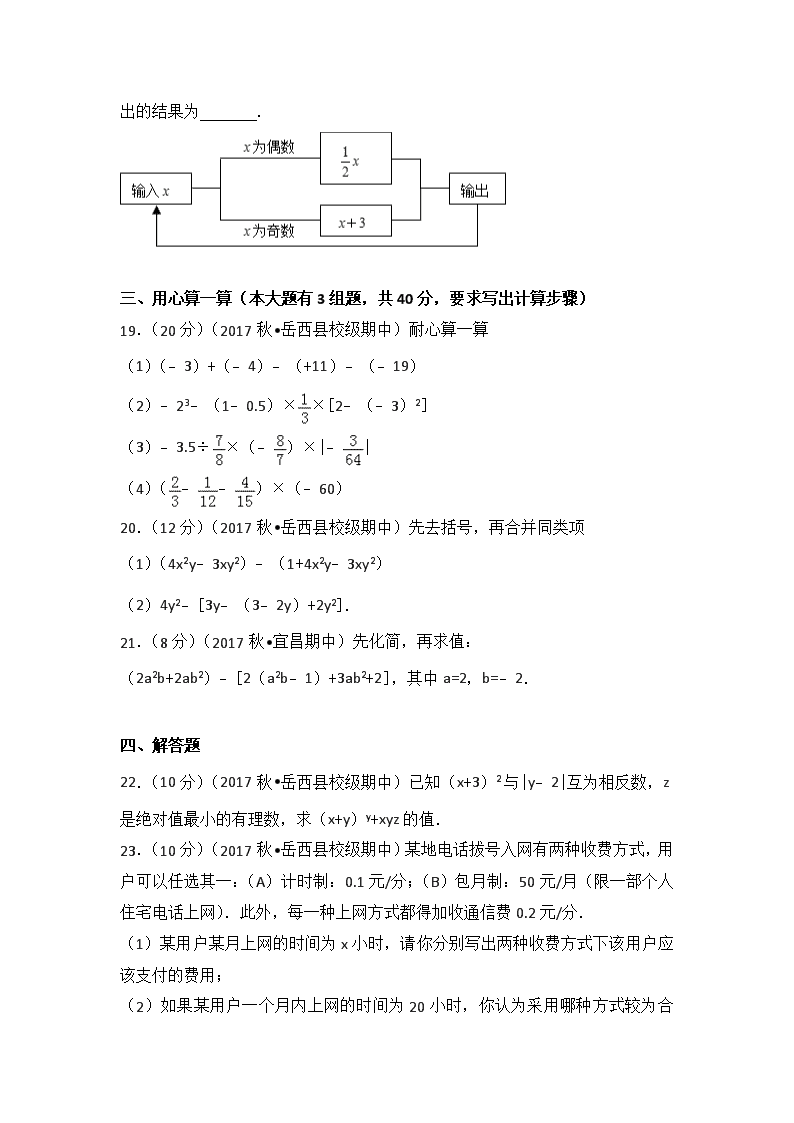
‎2017-2018学年安徽省安庆市岳西县冶溪中学七年级（上）期中数学试卷 ‎　‎ 一、精心选一选（本大题共8题，每小题3分，共24分．）‎ ‎1．（3分）（2016秋•孝南区期中）夏汛期间，某条河流的最高水位高出警戒线水位2.5米，最低水位低于警戒线水位1.5米，则这期间最高水位比最低水位高（　　）‎ A．1米 B．4米 C．﹣1米 D．﹣4米 ‎2．（3分）（2016秋•孝南区期中）下列运算正确的是（　　）‎ A．2a+3b=5ab B．2a﹣3b=﹣1 C．2a2b﹣2ab2=0 D．2ab﹣2ba=0‎ ‎3．（3分）（2016秋•孝南区期中）在数轴上，点A表示﹣3，从点A出发，沿数轴移动4个单位长度到达点B，则点B表示的数是（　　）‎ A．﹣7 B．1 C．4 D．﹣7或1‎ ‎4．（3分）（2010•烟台）据统计，截止5月31日上海世博会累计入园人数为803万．这个数字用科学记数法表示为（　　）‎ A．8×106 B．8.03×106 C．8.03×107 D．803×104‎ ‎5．（3分）（2016秋•嵊州市期末）绝对值大于2且小于5的所有整数的和是（　　）‎ A．0 B．7 C．14 D．28‎ ‎6．（3分）（2012秋•黄冈期末）若3＜a＜4时，化简|a﹣3|+|a﹣4|=（　　）‎ A．2a﹣7 B．2a﹣1 C．1 D．7‎ ‎7．（3分）（2012秋•海陵区期末）已知代数式x+2y+1的值是3，则代数式2x+4y+1的值是（　　）‎ A．4 B．5 C．7 D．不能确定 ‎8．（3分）（2010•淮安）观察下列各式：‎ ‎，‎ ‎，‎ ‎，‎ ‎…‎ 计算：3×（1×2+2×3+3×4+…+99×100）=（　　）‎ A．97×98×99 B．98×99×100 C．99×100×101 D．100×101×102‎ ‎　‎ 二、细心填一填（本大题共10题，每小题3分，共30分）‎ ‎9．（3分）（2010秋•邗江区期中）如果﹣20%表示减少20%，那么+6%表示　 　．‎ ‎10．（3分）（2010秋•甘井子区期末）单项式的系数是　 　．‎ ‎11．（3分）（2015秋•东台市期中）表示“x与4的差的3倍”的代数式为　 　．‎ ‎12．（3分）（2016秋•嵊州市期末）若3am+2b4与﹣a5bn﹣1的和仍是一个单项式，则m+n=　 　．‎ ‎13．（3分）（2010秋•邗江区期中）多项式3x|m|y2+（m+2）x2y﹣1是四次三项式，则m的值为　 　．‎ ‎14．（3分）（2010秋•斗门区校级期中）化简：﹣（5x+3y）+（7y﹣x）=　 　．‎ ‎15．（3分）（2017秋•江都区期中）若关于a，b的多项式2（a2﹣2ab﹣b2）﹣（a2+mab+2b2）不含ab项，则m=　 　．‎ ‎16．（3分）（2014秋•栾城县校级期中）M、N是数轴上的二个点，线段MN的长度为2，若点M表示的数为﹣1，则点N表示的数为　 　．‎ ‎17．（3分）（2010秋•邗江区期中）有一列数a1，a2，a3，…，an，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a1=2，则a2007为　 　．‎ ‎18．（3分）（2012•盐城二模）如图所示的运算程序中，若开始输入的x值为48，我们发现第一次输出的结果为24，第二次输出的结果为12，…，则第2010次输出的结果为　 　．‎ ‎　‎ 三、用心算一算（本大题有3组题，共40分，要求写出计算步骤）‎ ‎19．（20分）（2017秋•岳西县校级期中）耐心算一算 ‎（1）（﹣3）+（﹣4）﹣（+11）﹣（﹣19）‎ ‎（2）﹣23﹣（1﹣0.5）××[2﹣（﹣3）2]‎ ‎（3）﹣3.5÷×（﹣）×|﹣|‎ ‎（4）（﹣﹣）×（﹣60）‎ ‎20．（12分）（2017秋•岳西县校级期中）先去括号，再合并同类项 ‎（1）（4x2y﹣3xy2）﹣（1+4x2y﹣3xy2）‎ ‎（2）4y2﹣[3y﹣（3﹣2y）+2y2]．‎ ‎21．（8分）（2017秋•宜昌期中）先化简，再求值：‎ ‎（2a2b+2ab2）﹣[2（a2b﹣1）+3ab2+2]，其中a=2，b=﹣2．‎ ‎　‎ 四、解答题 ‎22．（10分）（2017秋•岳西县校级期中）已知（x+3）2与|y﹣2|互为相反数，z是绝对值最小的有理数，求（x+y）y+xyz的值．‎ ‎23．（10分）（2017秋•岳西县校级期中）某地电话拔号入网有两种收费方式，用户可以任选其一：（A）计时制：0.1元/分；（B）包月制：50元/月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通信费0.2元/分．‎ ‎（1）某用户某月上网的时间为x小时，请你分别写出两种收费方式下该用户应该支付的费用；‎ ‎（2）如果某用户一个月内上网的时间为20小时，你认为采用哪种方式较为合算？‎ ‎24．（12分）（2010秋•邗江区期中）（1）例：代数式（a+b）2表示a、b两数和的平方．仿照上例填空：‎ 代数式a2﹣b2表示　 　．‎ 代数式（a+b）（a﹣b）表示　 　．‎ ‎（2）试计算a、b取不同数值时，a2﹣b2及（a+b）（a﹣b）的植，填入下表：‎ ‎（3）请你再任意给a、b各取一个数值，并计算a2﹣b2及（a+b）（a﹣b）的植：‎ 当a=　 　，b=　 　时，a2﹣b2=　 　，（a+b）（a﹣b）=　 　．‎ ‎（4）我的发现：　 　．‎ ‎（5）用你发现的规律计算：78.352﹣21.652．‎ ‎25．（12分）（2015秋•岳阳校级期中）如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中 ‎（1）A→C（　 　，　 　），B→C（　 　，　 　），‎ C→D （　 　，　 　）；‎ ‎（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的最少路程；‎ ‎（3）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置．‎ ‎26．（12分）（2012秋•张家港市期中）某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：‎ 星期 一 二 三 四 五 六 日 增减 ‎+5‎ ‎﹣2‎ ‎﹣4‎ ‎+12‎ ‎﹣10‎ ‎+16‎ ‎﹣9‎ ‎（1）根据记录的数据可知该厂星期六生产自行车　 　_辆；‎ ‎（2）根据记录的数据可知该厂本周实际生产自行车　 　辆；‎ ‎（3）产量最多的一天比产量最少的一天多生产自行车　 　辆；‎ ‎（4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？‎ ‎　‎ ‎2017-2018学年安徽省安庆市岳西县冶溪中学七年级（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、精心选一选（本大题共8题，每小题3分，共24分．）‎ ‎1．（3分）（2016秋•孝南区期中）夏汛期间，某条河流的最高水位高出警戒线水位2.5米，最低水位低于警戒线水位1.5米，则这期间最高水位比最低水位高（　　）‎ A．1米 B．4米 C．﹣1米 D．﹣4米 ‎【分析】根据有理数的减法，即可解答．‎ ‎【解答】解：根据题意，得：2.5﹣（﹣1.5）=2.5+1.5=4，‎ 故选：B．‎ ‎【点评】本题考查了有理数的减法，解决本题的关键是熟记有理数的减法．‎ ‎　‎ ‎2．（3分）（2016秋•孝南区期中）下列运算正确的是（　　）‎ A．2a+3b=5ab B．2a﹣3b=﹣1 C．2a2b﹣2ab2=0 D．2ab﹣2ba=0‎ ‎【分析】直接利用合并同类项的知识求解即可求得答案．‎ ‎【解答】解：A、不是同类项不能合并，故A错误；‎ B、不是同类项不能合并，故B错误；‎ C、把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，故C错误；‎ D、把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，故D正确；‎ 故选：D．‎ ‎【点评】此题考查了合并同类项的法则．注意合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．‎ ‎　‎ ‎3．（3分）（2016秋•孝南区期中）在数轴上，点A表示﹣3，从点A出发，沿数轴移动4个单位长度到达点B，则点B表示的数是（　　）‎ A．﹣7 B．1 C．4 D．﹣7或1‎ ‎【分析】先根据点A所表示的数，再分两种情况进行讨论，当点A沿数轴向右移动和点A沿数轴向左移动时，列出式子，求出点B表示的数．‎ ‎【解答】解：∵点A表示﹣3，‎ ‎∴从点A出发，沿数轴向右移动4个单位长度到达B点，则点B表示的数是﹣3+4=1；‎ ‎∴从点A出发，沿数轴向左移动4个单位长度到达B点，则点B表示的数是﹣3﹣4=﹣7；‎ ‎∴点B表示的数是1或﹣7．‎ 故选：D．‎ ‎【点评】此题考查了数轴，解题的关键根据题意列出式子，再根据有理数的加减法法则进行计算，要考虑两种情况，不要漏掉．‎ ‎　‎ ‎4．（3分）（2010•烟台）据统计，截止5月31日上海世博会累计入园人数为803万．这个数字用科学记数法表示为（　　）‎ A．8×106 B．8.03×106 C．8.03×107 D．803×104‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于1时，n是正数；当原数的绝对值小于1时，n是负数．‎ ‎【解答】解：803万=8 030 000=8.03×106．‎ 故选：B．‎ ‎【点评】此题考查科学记数法的表示方法，科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎5．（3分）（2016秋•嵊州市期末）绝对值大于2且小于5的所有整数的和是（　　）‎ A．0 B．7 C．14 D．28‎ ‎【分析】绝对值绝对值大于2且小于5的所有整数就是在数轴上﹣5与﹣2之间和2与5之间的所有整数，即可求得各个数的和．‎ ‎【解答】解：绝对值大于2且小于5的所有整数是：﹣4，﹣3，3，4．‎ 则﹣4+（﹣3）+3+4=0‎ 故选：A．‎ ‎【点评】本题考查了有理数的加法，正确根据绝对值，结合数轴确定所有的整数，是解决本题的关键．‎ ‎　‎ ‎6．（3分）（2012秋•黄冈期末）若3＜a＜4时，化简|a﹣3|+|a﹣4|=（　　）‎ A．2a﹣7 B．2a﹣1 C．1 D．7‎ ‎【分析】因为3＜a＜4，则有|a﹣3|=a﹣3，|a﹣4|=4﹣a，再化简给出的式子即可．‎ ‎【解答】解：∵3＜a＜4，‎ ‎∴|a﹣3|=a﹣3，|a﹣4|=4﹣a，‎ ‎∴|a﹣3|+|a﹣4|=a﹣3+4﹣a=1．‎ 故选：C．‎ ‎【点评】主要考查了绝对值的运算，先确定绝对值符号中代数式的正负再去绝对值符号．‎ ‎　‎ ‎7．（3分）（2012秋•海陵区期末）已知代数式x+2y+1的值是3，则代数式2x+4y+1的值是（　　）‎ A．4 B．5 C．7 D．不能确定 ‎【分析】先根据已知条件易求x+2y的值，再将所求代数式提取公因数2，最后把x+2y的值代入计算即可．‎ ‎【解答】解：根据题意得 x+2y+1=3，‎ ‎∴x+2y=2，‎ 那么2x+4y+1=2（x+2y）+1=2×2+1=5．‎ 故选：B．‎ ‎【点评】本题考查了代数式求值，解题的关键是整体代入．‎ ‎　‎ ‎8．（3分）（2010•淮安）观察下列各式：‎ ‎，‎ ‎，‎ ‎，‎ ‎…‎ 计算：3×（1×2+2×3+3×4+…+99×100）=（　　）‎ A．97×98×99 B．98×99×100 C．99×100×101 D．100×101×102‎ ‎【分析】先根据题中所给的规律，把式子中的1×2，2×3，…99×100，分别展开，整理后即可求解．注意：1×2=×（1×2×3）．‎ ‎【解答】解：根据题意可知 ‎3×（1×2+2×3+3×4+…+99×100）‎ ‎=3×[×（1×2×3﹣0×1×2）+（2×3×4﹣1×2×3）+（3×4×5﹣2×3×4）+…+（99×100×101﹣98×99×100）]‎ ‎=1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+99×100×101﹣98×99×100‎ ‎=99×100×101．‎ 故选：C．‎ ‎【点评】通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力．‎ ‎　‎ 二、细心填一填（本大题共10题，每小题3分，共30分）‎ ‎9．（3分）（2010秋•邗江区期中）如果﹣20%表示减少20%，那么+6%表示　增加6%　．‎ ‎【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．‎ ‎【解答】解：“正”和“负”相对，‎ 如果﹣20%表示减少20%，那么+6%表示增加6%．‎ ‎【点评】解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．‎ ‎　‎ ‎10．（3分）（2010秋•甘井子区期末）单项式的系数是　　．‎ ‎【分析】根据单项式系数的定义来求解．单项式中数字因数叫做单项式的系数．‎ ‎【解答】解：单项式的系数是．‎ 故答案为．‎ ‎【点评】本题考查了单项式系数的定义．确定单项式的系数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数的关键．‎ ‎　‎ ‎11．（3分）（2015秋•东台市期中）表示“x与4的差的3倍”的代数式为　3（x﹣4）　．‎ ‎【分析】先求差，然后求倍数．‎ ‎【解答】解：x与4的差为，差的3倍为：3（x﹣4）．‎ 故答案为：3（x﹣4）．‎ ‎【点评】列代数式的关键是正确理解文字语言中的关键词，比如该题中的“倍”、“和”等，从而明确其中的运算关系，正确地列出代数式．‎ ‎　‎ ‎12．（3分）（2016秋•嵊州市期末）若3am+2b4与﹣a5bn﹣1的和仍是一个单项式，则m+n=　8　．‎ ‎【分析】两者可以合并说明两式为同类项，根据同类项的字母相同及相同字母的指数相同可得出m和n的值．‎ ‎【解答】解：由题意得，两者可以合并说明两式为同类项，‎ 可得m+2=5，n﹣1=4，‎ 解得：m=3，n=5，m+n=8．‎ 故填：8．‎ ‎【点评】本题考查同类项的知识，难度不大，掌握同类项的字母相同及相同字母的指数相同是关键．‎ ‎　‎ ‎13．（3分）（2010秋•邗江区期中）多项式3x|m|y2+（m+2）x2y﹣1是四次三项式，则m的值为　2　．‎ ‎【分析】根据四次三项式的定义可知，该多项式的最高次数为4，项数是3，所以可确定m的值．‎ ‎【解答】解：∵多项式3x|m|y2+（m+2）x2y﹣1是四次三项式，‎ ‎∴|m|+2=4，m+2≠0，‎ ‎∴|m|=2，且m≠﹣2，‎ ‎∴m=2．‎ 故答案为：2‎ ‎【点评】本题考查了与多项式有关的概念，解题的关键理解四次三项式的概念，多项式中每个单项式叫做多项式的项，有几项叫几项式，这些单项式中的最高次数，就是这个多项式的次数．‎ ‎　‎ ‎14．（3分）（2010秋•斗门区校级期中）化简：﹣（5x+3y）+（7y﹣x）=　﹣6x+4y　．‎ ‎【分析】‎ 本题为整式的加减，先去括号，注意正负号的变化，然后再合并同类项得出答案．‎ ‎【解答】解：原式=﹣5x﹣3y+7y﹣x ‎=﹣6x+4y；‎ 故此题应该填﹣6x+4y．‎ ‎【点评】考查了去括号法则以及合并同类项法则．‎ ‎　‎ ‎15．（3分）（2017秋•江都区期中）若关于a，b的多项式2（a2﹣2ab﹣b2）﹣（a2+mab+2b2）不含ab项，则m=　﹣4　．‎ ‎【分析】先整理整式，不含ab项及ab项的系数为0，由此可得出m的值．‎ ‎【解答】解：2（a2﹣2ab﹣b2）﹣（a2+mab+2b2）=a2﹣（4+m）ab﹣4b2，‎ 又∵不含ab项，故4+m=0，m=﹣4．‎ 故填：﹣4．‎ ‎【点评】本题考查整式的加减，关键是对整式的整理，难度不大．‎ ‎　‎ ‎16．（3分）（2014秋•栾城县校级期中）M、N是数轴上的二个点，线段MN的长度为2，若点M表示的数为﹣1，则点N表示的数为　﹣3，1　．‎ ‎【分析】根据题意，正确画出图形，可分两种情况讨论：‎ ‎（1）N在M的左边；‎ ‎（2）N在M的右边．‎ ‎【解答】解：如图，N的位置不确定：‎ ‎（1）N在M的左边，可以看出点N表示的数为﹣3；‎ ‎（2）N在M的右边，可以看出点N表示的数为1．‎ ‎∴点N表示的数为﹣3或1．‎ 故答案为：﹣3，1．‎ ‎【点评】本题主要考查了数轴的概念，属于基础性题目，比较简单．‎ ‎　‎ ‎17．（3分）（2010秋•邗江区期中）有一列数a1，a2，a3，…，an，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a1=2，则a2007为　﹣1　．‎ ‎【分析】题中已经给出了规律，根据规律分别表示出各个数，再进行分析从而发现新的规律，根据规律解题即可．‎ ‎【解答】解：∵a1=2‎ ‎∴a2=1﹣=，a3=1﹣=1﹣2=﹣1，a4=1﹣（﹣1）=2，a5=1﹣=，a6=1﹣2=﹣1，a7=1﹣（﹣1）=2…‎ ‎∵从第二项开始每三个循环一次，（2007﹣1）除以3余数为2．‎ ‎∴a2007=﹣1．‎ ‎【点评】此题主要考查学生对规律型题的掌握，做此题需注意是从第二项起每三个数循环一次．‎ ‎　‎ ‎18．（3分）（2012•盐城二模）如图所示的运算程序中，若开始输入的x值为48，我们发现第一次输出的结果为24，第二次输出的结果为12，…，则第2010次输出的结果为　3　．‎ ‎【分析】根据运算程序可推出第三次输出的结果为6，第四次输出的结果为3，第五次输出的结果为6，第六次输出的结果为3，…，依此类推，即可推出从第三次开始，第偶数次输出的为3，第奇数次输出的为6，可得第2010此输出的结果为3．‎ ‎【解答】解：∵第二次输出的结果为12，‎ ‎∴第三次输出的结果为6，第四次输出的结果为3，第五次输出的结果为6，第六次输出的结果为3，…，‎ ‎∴从第三次开始，第偶数次输出的为3，第奇数次输出的为6，‎ ‎∴第2010次输出的结果为3．‎ 故答案为3．‎ ‎【点评】本题主要要考查有理数的乘法和加法运算，关键在于每次输出的结果总结出规律．‎ ‎　‎ 三、用心算一算（本大题有3组题，共40分，要求写出计算步骤）‎ ‎19．（20分）（2017秋•岳西县校级期中）耐心算一算 ‎（1）（﹣3）+（﹣4）﹣（+11）﹣（﹣19）‎ ‎（2）﹣23﹣（1﹣0.5）××[2﹣（﹣3）2]‎ ‎（3）﹣3.5÷×（﹣）×|﹣|‎ ‎（4）（﹣﹣）×（﹣60）‎ ‎【分析】（1）原式利用减法法则变形，计算即可求出值；‎ ‎（2）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可求出值；‎ ‎（3）原式利用乘除法则计算即可求出值；‎ ‎（4）原式利用乘法分配律计算即可求出值．‎ ‎【解答】解：（1）原式=﹣3﹣4﹣11+19=﹣18+19=1； ‎ ‎（2）原式=﹣8+=﹣；‎ ‎（3）原式=×××=； ‎ ‎（4）原式=﹣40+5+16=﹣19．‎ ‎【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎20．（12分）（2017秋•岳西县校级期中）先去括号，再合并同类项 ‎（1）（4x2y﹣3xy2）﹣（1+4x2y﹣3xy2）‎ ‎（2）4y2﹣[3y﹣（3﹣2y）+2y2]．‎ ‎【分析】（1）首先去括号，进而合并同类项得出答案；‎ ‎（2）首先去括号，进而合并同类项得出答案．‎ ‎【解答】解：（1）（4x2y﹣3xy2）﹣（1+4x2y﹣3xy2）‎ ‎=4x2y﹣3xy2﹣1﹣4x2y+3xy2‎ ‎=﹣1；‎ ‎（2）4y2﹣[3y﹣（3﹣2y）+2y2]‎ ‎=4y2﹣（3y﹣3+2y+2y2）‎ ‎=4y2﹣5y+3﹣2y2‎ ‎=2y2﹣5y+3．‎ ‎【点评】此题主要考查了整式的加减运算，正确掌握合并同类项法则是解题关键．‎ ‎　‎ ‎21．（8分）（2017秋•宜昌期中）先化简，再求值：‎ ‎（2a2b+2ab2）﹣[2（a2b﹣1）+3ab2+2]，其中a=2，b=﹣2．‎ ‎【分析】本题应对代数式进行去括号，合并同类项，将代数式化为最简式，然后把a，b的值代入即可．注意去括号时，如果括号前是负号，那么括号中的每一项都要变号；合并同类项时，只把系数相加减，字母与字母的指数不变．‎ ‎【解答】解：（2a2b+2ab2）﹣[2（a2b﹣1）+3ab2+2]‎ ‎=2a2b+2ab2﹣（2a2b﹣2+3ab2+2）‎ ‎=2a2b+2ab2﹣2a2b﹣3ab2‎ ‎=﹣ab2，‎ 当a=2，b=﹣2时，‎ 原式=﹣2×（﹣2）2=﹣8．‎ ‎【点评】考查了整式的加减﹣化简求值，此题关键在去括号．①运用乘法分配律时不要漏乘；②括号前面是“﹣”号，去掉括号和它前面的“﹣”号，括号里面的各项都要变号．‎ ‎　‎ 四、解答题 ‎22．（10分）（2017秋•岳西县校级期中）已知（x+3）2与|y﹣2|互为相反数，z是绝对值最小的有理数，求（x+y）y+xyz的值．‎ ‎【分析】思想确定x、y、z的值，再代入计算即可．‎ ‎【解答】解：∵（x+3）2与|y﹣2|互为相反数，‎ ‎∴（x+3）2+|y﹣2|=0，‎ 又∵（x+3）2≥0，|y﹣2|≥0，‎ ‎∴x=﹣3，y=2，‎ ‎∵z是绝对值最小的有理数，‎ ‎∴z=0，‎ ‎∴（x+y）y+xyz=（﹣3+2）2+0=1．‎ ‎【点评】本题考查有理数的混合运算、非负数的性质、互为相反数的性质等知识，解题的关键是学会用转化的思想思考问题，属于中考常考题型．‎ ‎　‎ ‎23．（10分）（2017秋•岳西县校级期中）某地电话拔号入网有两种收费方式，用户可以任选其一：（A）计时制：0.1元/分；（B）包月制：50元/月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通信费0.2元/分．‎ ‎（1）某用户某月上网的时间为x小时，请你分别写出两种收费方式下该用户应该支付的费用；‎ ‎（2）如果某用户一个月内上网的时间为20小时，你认为采用哪种方式较为合算？‎ ‎【分析】（1）第一种是费用=每分钟的费用×时间+通信费，第二种的费用=月费+通信费．‎ ‎（2）将20小时分别代入（1）计算出费用的大小，再进行比较就可以得出结论．‎ ‎【解答】（1）采用计时制应付的费用为（0.1+0.2）×60×x=18x（元），‎ 采用包月制应付的费用为50+0.2•x•60=50+12x（元）；‎ ‎（2）若一个月内上网的时间为20小时，‎ 则计时制应付的费用为18×20=360（元），‎ 包月制应付的费用为50+12×20=290（元）．‎ 很明显，包月制合算．‎ ‎【点评】本题考查了列代数式，表示费用的时候注意单位的统一．解决问题的关键是读懂题意，找到所求的量的等量关系．‎ ‎　‎ ‎24．（12分）（2010秋•邗江区期中）（1）例：代数式（a+b）2表示a、b两数和的平方．仿照上例填空：‎ 代数式a2﹣b2表示　a、b两数平方的差　．‎ 代数式（a+b）（a﹣b）表示　a、b两数的和与两数的差的积　．‎ ‎（2）试计算a、b取不同数值时，a2﹣b2及（a+b）（a﹣b）的植，填入下表：‎ ‎（3）请你再任意给a、b各取一个数值，并计算a2﹣b2及（a+b）（a﹣b）的植：‎ 当a=　2　，b=　1　时，a2﹣b2=　3　，（a+b）（a﹣b）=　3　．‎ ‎（4）我的发现：　a2﹣b2=（a+b）（a﹣b）　．‎ ‎（5）用你发现的规律计算：78.352﹣21.652．‎ ‎【分析】（1）根据两式的意义即可写出；‎ ‎（2）分别代入求值即可；‎ ‎（3）任意给a、b各取一个数值，代入求值，即可；‎ ‎（4）根据前边的计算，总结出a2﹣b2与（a+b）（a﹣b）的大小关系即可；‎ ‎（5）利用（4）中的关系，计算即可．‎ ‎【解答】解：（1）a、b两数平方的差；a、b两数的和与两数的差的积；（2分）‎ ‎（2）（3分）‎ ‎（3）a=2，b=1时，a2﹣b2=3，（a+b）（a﹣b）=3；‎ ‎（4）a2﹣b2=（a+b）（a﹣b）；（2分）‎ ‎（5）78.352﹣21.652=（78.35+21.65）（78.35﹣21.65）=5670．（3分）‎ ‎【点评】本题主要是通过实例探究了平方差公式，正确理解题目每部提出的要求是解决本题的关键．‎ ‎　‎ ‎25．（12分）（2015秋•岳阳校级期中）如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中 ‎（1）A→C（　+3　，　+4　），B→C（　+2　，　0　），‎ C→D （　+1　，　﹣2　）；‎ ‎（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的最少路程；‎ ‎（3）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置．‎ ‎【分析】（1）根据第一个数表示左右方向，第二个数表示上下方向结合图形写出即可；‎ ‎（2）根据行走路线列出算式计算即可得解；‎ ‎（3）根据方格和标记方法作出线路图即可得解．‎ ‎【解答】解：（1）A→C（+3，+4），B→C（+2，0），C→D（+1，﹣2）；‎ ‎（2）1+4+2+1+2=10；‎ ‎（3）点P如图所示．‎ ‎【点评】本题考查了坐标确定位置，读懂题目信息，理解行走路线的记录方法是解题的关键．‎ ‎　‎ ‎26．（12分）（2012秋•张家港市期中）某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：‎ 星期 一 二 三 四 五 六 日 增减 ‎+5‎ ‎﹣2‎ ‎﹣4‎ ‎+12‎ ‎﹣10‎ ‎+16‎ ‎﹣9‎ ‎（1）根据记录的数据可知该厂星期六生产自行车　216　_辆；‎ ‎（2）根据记录的数据可知该厂本周实际生产自行车　1408　辆；‎ ‎（3）产量最多的一天比产量最少的一天多生产自行车　26　辆；‎ ‎（4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？‎ ‎【分析】（1）用200加上增减的+16即可；‎ ‎（2）先把增减的量都相加，然后根据有理数的加法运算法则进行计算，再加上计划生产量即可；‎ ‎（3）用最多的星期六的量减去最少的星期五的量，根据有理数的减法运算计算即可；‎ ‎（4）根据规定列出算式，然后根据有理数的混合运算方法进行计算即可求解．‎ ‎【解答】解：（1）200+（+16）=216；‎ ‎（2）∵（+5）+（﹣2）+（﹣4）+（+12）+（﹣10）+（+16）+（﹣9），‎ ‎=5﹣2﹣4+12﹣10+16﹣9，‎ ‎=33﹣25，‎ ‎=8，‎ ‎∴1400+8=1408；‎ ‎（3）（+16）﹣（﹣10），‎ ‎=16+10，‎ ‎=26；‎ ‎（4）50×1408+8×15，‎ ‎=70400+120，‎ ‎=70520．‎ 故答案为：（1）216，（2）1408，（3）26，（4）70520．‎ ‎【点评】‎ 本题考查了正数与负数，有理数加减混合运算，读懂表格数据，根据题意准确列式是解题的关键．‎ ‎　‎