用正多边形铺设地面教案1

用正多边形铺设地面教案1

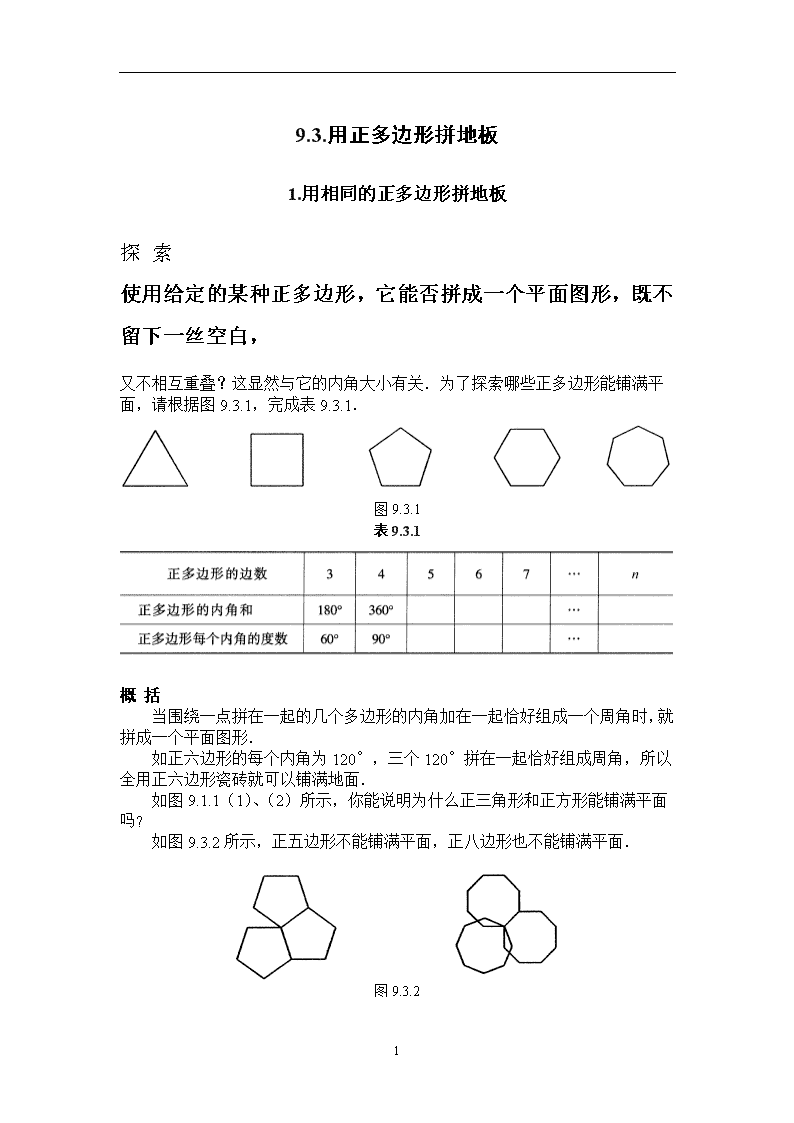
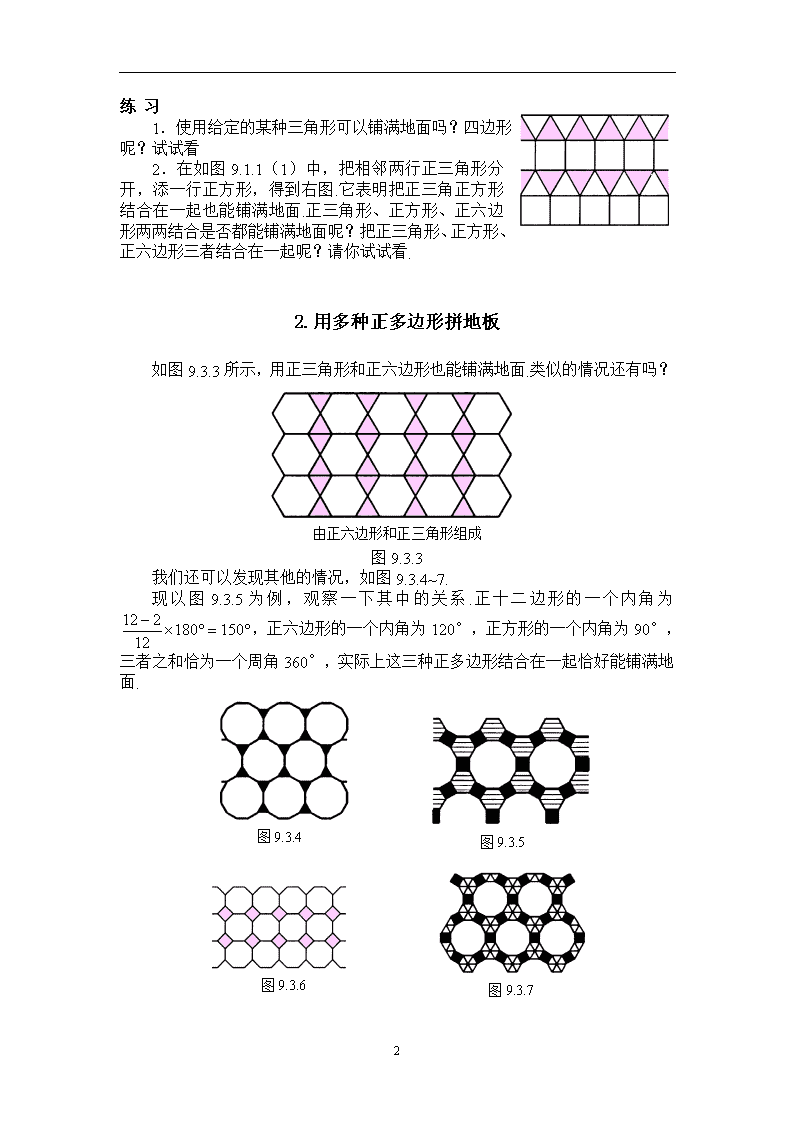
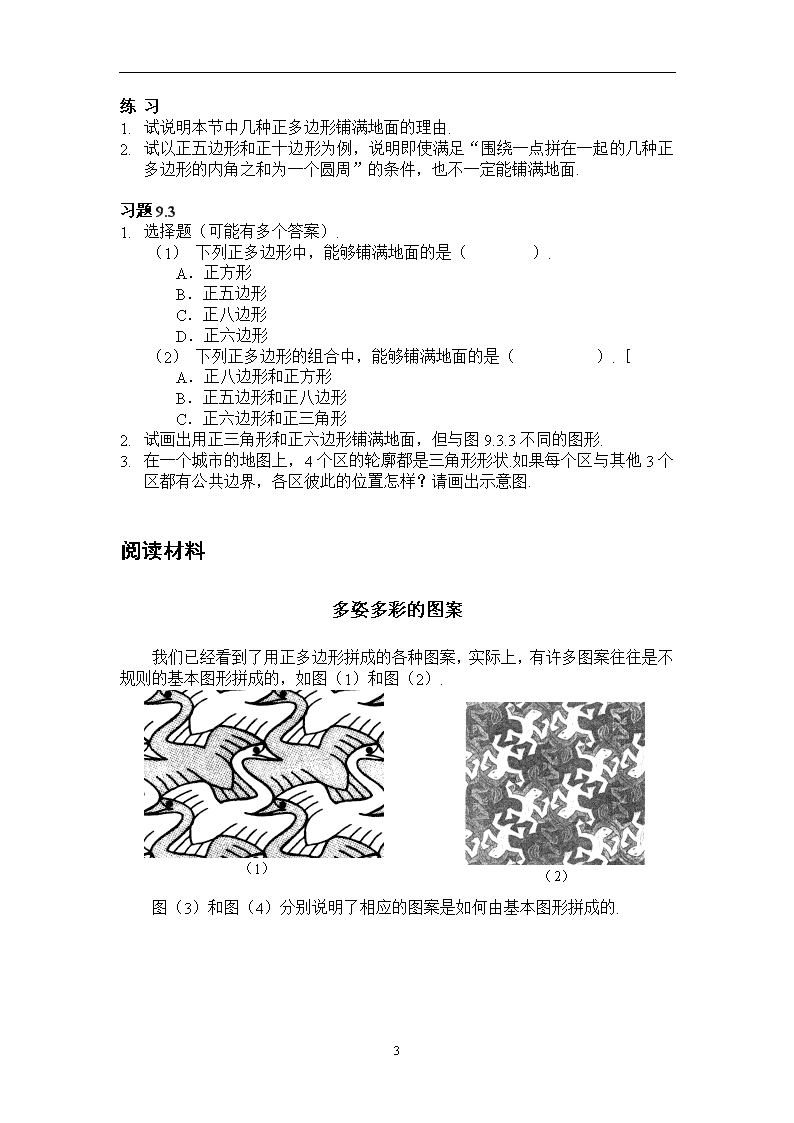
‎ ‎ ‎9.3.用正多边形拼地板 ‎1.用相同的正多边形拼地板 探 索 使用给定的某种正多边形，它能否拼成一个平面图形，既不留下一丝空白，‎ 又不相互重叠？这显然与它的内角大小有关．为了探索哪些正多边形能铺满平 面，请根据图9.3.1，完成表9.3.1．‎ 图9.3.1‎ 表9.3.1‎ 概 括 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时，就 拼成一个平面图形． 如正六边形的每个内角为120°，三个120°拼在一起恰好组成周角，所以 全用正六边形瓷砖就可以铺满地面． 如图9.1.1（1）、（2）所示，你能说明为什么正三角形和正方形能铺满平面 吗? 如图9.3.2所示，正五边形不能铺满平面，正八边形也不能铺满平面． ‎ 4‎ ‎ ‎ 练 习 ‎1．使用给定的某种三角形可以铺满地面吗？四边形呢？试试看.‎ ‎2．在如图9.1.1（1）中，把相邻两行正三角形分开，添一行正方形，得到右图.它表明把正三角正方形结合在一起也能铺满地面.正三角形、正方形、正六边形两两结合是否都能铺满地面呢？把正三角形、正方形、正六边形三者结合在一起呢？请你试试看.‎ ‎2.用多种正多边形拼地板 如图9.3.3所示，用正三角形和正六边形也能铺满地面.类似的情况还有吗？‎ 图9.3.3‎ 我们还可以发现其他的情况，如图9.3.4~7.‎ 现以图9.3.5为例，观察一下其中的关系.正十二边形的一个内角为，正六边形的一个内角为120°，正方形的一个内角为90°，三者之和恰为一个周角360°，实际上这三种正多边形结合在一起恰好能铺满地面.‎ ‎　　‎ ‎　　　‎ 4‎ ‎ ‎ 练 习 1. 试说明本节中几种正多边形铺满地面的理由.‎ 2. 试以正五边形和正十边形为例，说明即使满足“围绕一点拼在一起的几种正多边形的内角之和为一个圆周”的条件，也不一定能铺满地面.‎ 习题9.3‎ 1. 选择题（可能有多个答案）.‎ （1） 下列正多边形中，能够铺满地面的是（　　　　）.‎ A． 正方形　　　　　　‎ B． 正五边形 C． 正八边形 D． 正六边形 （2） 下列正多边形的组合中，能够铺满地面的是（　　　　　）.［‎ A． 正八边形和正方形 B． 正五边形和正八边形 C． 正六边形和正三角形 2. 试画出用正三角形和正六边形铺满地面，但与图9.3.3不同的图形.‎ 3. 在一个城市的地图上，4个区的轮廓都是三角形形状.如果每个区与其他3个区都有公共边界，各区彼此的位置怎样？请画出示意图.‎ 阅读材料 多姿多彩的图案 我们已经看到了用正多边形拼成的各种图案，实际上，有许多图案往往是不规则的基本图形拼成的，如图（1）和图（2）.‎ 图（3）和图（4）分别说明了相应的图案是如何由基本图形拼成的.‎ 4‎ ‎ ‎ ‎‎ 你玩过哪些拼图？你自己有设计出一幅拼图吗？‎ 4‎