平方差公式　教案(3)

平方差公式　教案(3)

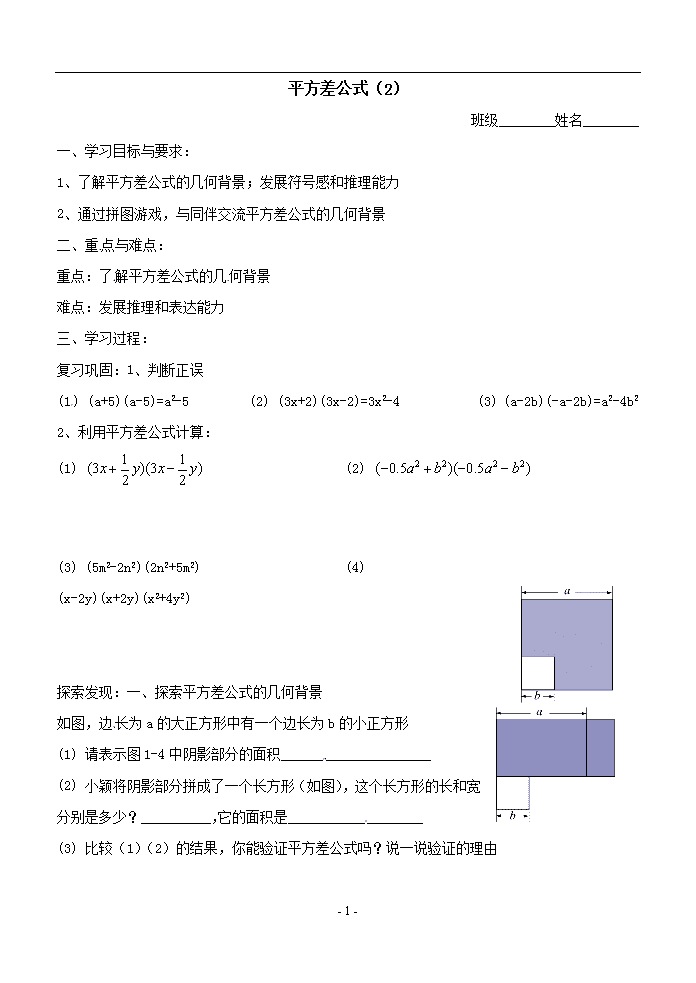
‎ ‎ 平方差公式（2）‎ 班级________姓名________‎ 一、学习目标与要求：‎ ‎1、了解平方差公式的几何背景；发展符号感和推理能力 ‎2、通过拼图游戏，与同伴交流平方差公式的几何背景 二、重点与难点：‎ 重点：了解平方差公式的几何背景 难点：发展推理和表达能力 三、学习过程：‎ 复习巩固：1、判断正误 ‎(1) (a+5)(a-5)=a2-5 (2) (3x+2)(3x-2)=3x2-4 (3) (a-2b)(-a-2b)=a2-4b2‎ ‎2、利用平方差公式计算：‎ ‎(1) (2) ‎ ‎(3) (5m2-2n2)(2n2+5m2) (4) (x-2y)(x+2y)(x2+4y2)‎ 探索发现：一、探索平方差公式的几何背景 如图，边长为a的大正方形中有一个边长为b的小正方形 ‎(1) 请表示图1-4中阴影部分的面积_____________________‎ ‎(2) 小颖将阴影部分拼成了一个长方形（如图），这个长方形的长和宽分别是多少？__________，它的面积是___________________‎ ‎(3) 比较（1）（2）的结果，你能验证平方差公式吗？说一说验证的理由 - 3 -‎ ‎ ‎ 二、利用平方差公式探索规律 ‎(1) 计算下列各组算式，并观察它们的共同特点 ‎ ‎ ‎(2) 从以上的过程中，你发现了什么规律？__________________________________________‎ ‎(3) 请用字母表示这一规律，你能说明它的正确性吗？‎ 三、巩固与提高 例1 用平方差公式进行计算 ‎(1) (2) ‎ 例2 计算：‎ ‎(1) (2) ‎ 练习1、计算：‎ ‎(1) (2) ‎ 练习2、计算：‎ ‎(1) (2) x(x+1)+(2-x)(2+x)‎ ‎(3) (3x-y)(3x+y)+y(x+y) (4) ‎ - 3 -‎ ‎ ‎ 例3 填空 ‎(1) a2-4=(a+2)( ) (2) 25-x2=(5-x)( ) (3) m2-n2=( )( )‎ 练习3 填空：‎ ‎(1) x2-25=( )( ) (2) 4m2-49=( )( )‎ ‎(3) a4-m4=(a2+m2)( )=(a2+m2)( )( )‎ 练习4 计算：‎ ‎(1) 123452-12346×12344 *(2) (22+1)(24+1)(28+1)(216+1)‎ 学习小结：给大家说一说你这节课的体会 - 3 -‎