- 2021-10-25 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020七年级数学上册 第4章余角和补角
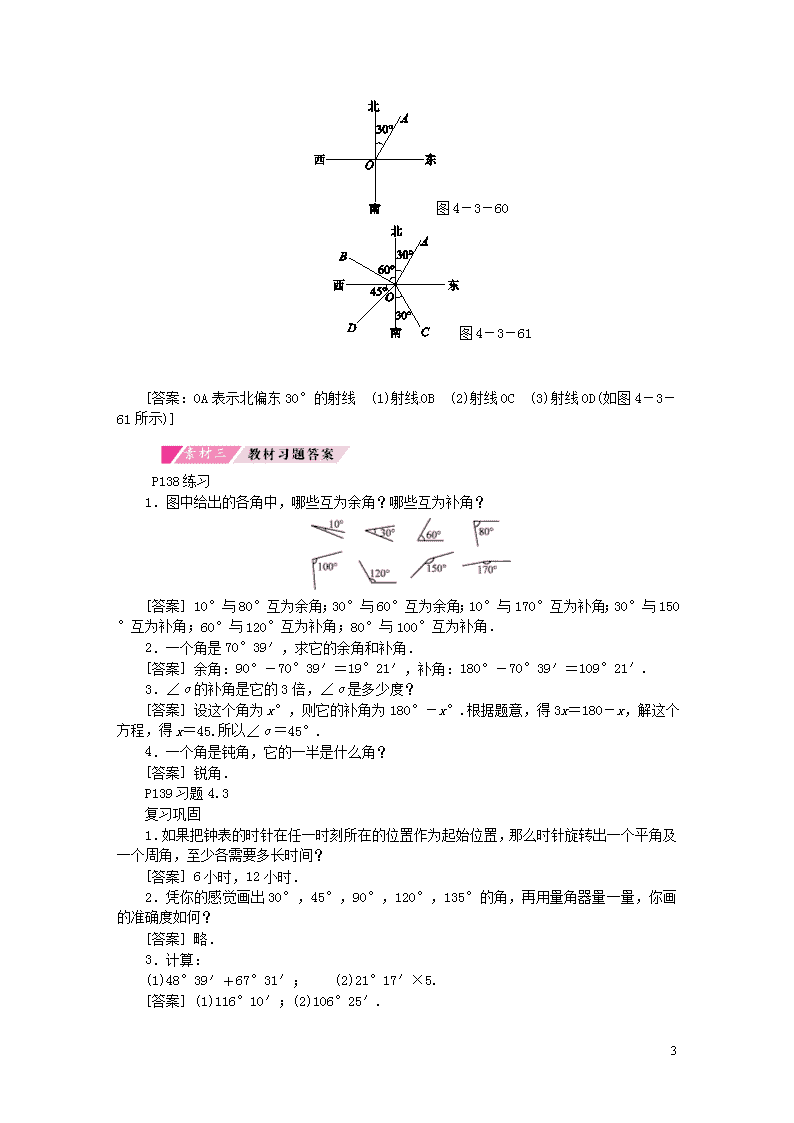
4.3 角 4.3.3 余角和补角 情景导入 置疑导入 归纳导入 复习导入 类比导入 悬念激趣 图4-3-58 情景导入 举世闻名的比萨斜塔位于意大利的比萨小镇,是一座由白色云石建成的古塔.该塔发生倾斜但斜而不倒,比萨因此远近闻名.比萨斜塔始建于1173年,从地面到塔顶高55米,自建成以后曾发生多次倾斜,常人只凭眼睛也能察觉.意大利科学家伽利略曾在斜塔的顶层做过自由落体运动的实验,开创了实验物理的新时代,斜塔也因而更加闻名遐迩.意大利政府曾想尽办法制止古塔的继续倾斜,但到目前为止未能成功.你知道斜塔的倾角是多少度吗?你能用什么方法测量呢?某位游客设计的测量斜塔倾角的方案是:将斜塔看成一条线段OA在正午太阳直射地面时标记塔顶的影子B,画出直线OB,想办法测出了∠AOB=85度,然后让学生思考: (1)斜塔OA倾斜了多少度?(2)斜塔OA与OC所成的角是多少度?(3)斜塔OA与OB所成的另外一个角即∠AOD是多少度? [说明与建议] 说明:从学生的兴趣着手,激发学生的探究欲望,给学生一种轻松的心理氛围,易于学生学习新知识,让学生注重观察生活,知道数学来源于生活,并服务于生活.建议:让学生自由组合,相互讨论,活跃课堂气氛,从他们的兴趣入手,让学生无形中参与到课堂的活动中,在学生的讨论探究中口头归纳出余角和补角的性质. 复习导入 (课件演示)计算: (1)44°+46°=__90_°__;(2)30°20′34″+59°39′26″=__90_°__; (3)10°+25°+55°=__90_°__;(4)96°+84°=__180_°__; (5)58°45′+121°15′=__180_°__. 学生计算并回答,总结它们的特点. [说明与建议] 说明:通过计算复习上节课的知识,设置悬念,调动学生的积极性,更进一步促使学生渴望尽快寻求到答案,同时也为判断余角和补角做铺垫.建议:教师应关注:计算的准确性,学生是否认真观察并思考. 15 [命题角度1] 直接运余角与补角的概念求角的度数 在计算时要紧扣余角、补角的定义进行计算.注意互余的两个角都是锐角,互补的两个角可能是一个是锐角,另一个是钝角;也可能两个角都是直角. 例 求35°42′角的余角和补角的度数. 解:余角的度数为90°-35°42′=54°18′;其补角的度数为180°-35°42′=144°18′. [命题角度2] 根据余角、补角的性质说理的问题 余角、补角的性质是:同角或等角的余角相等,同角或等角的补角相等.这个性质也为说明两个角相等提供了思路.认真观察分析图形,挖掘出图形中隐含的数量关系是关键. 例1 已知∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4有什么关系?说说理由. 解:由∠1与∠2互补,∠3和∠4互补,得∠1+∠2=180°,∠3+∠4=180°,又∠1=∠3,根据等角的补角相等,可知∠2=∠4. 图4-3-59 例2 如图4-3-59,点E,O,A在同一直线上,∠AOB=∠COD=90°,那么图中与∠AOD互补的角为__∠DOE,∠BOC__. [解析] 因为∠DOE+∠AOD=180°,所以∠DOE与∠AOD互为补角.根据∠AOB=∠COD=90°,可得出∠DOE=∠BOC,所以∠BOC+∠AOD=180°,所以∠BOC与∠AOD互为补角.这样,∠AOD的补角有两个分别是:∠DOE,∠BOC. [命题角度3] 用角度表示方向 方位角是以南北方向为起始方向,一般是以北偏东,南偏西等加上角度来表示的.特殊的方位角如下: 例 如图4-3-60,OA表示什么方向的一条射线?并画出表示下列方向的射线. (1)北偏西60°;(2)南偏东30°;(3)西南方向. 15 图4-3-60 图4-3-61 [答案:OA表示北偏东30°的射线 (1)射线OB (2)射线OC (3)射线OD(如图4-3-61所示)] P138练习 1.图中给出的各角中,哪些互为余角?哪些互为补角? [答案] 10°与80°互为余角;30°与60°互为余角;10°与170°互为补角;30°与150°互为补角;60°与120°互为补角;80°与100°互为补角. 2.一个角是70°39′,求它的余角和补角. [答案] 余角:90°-70°39′=19°21′,补角:180°-70°39′=109°21′. 3.∠α的补角是它的3倍,∠α是多少度? [答案] 设这个角为x°,则它的补角为180°-x°.根据题意,得3x=180-x,解这个方程,得x=45.所以∠α=45°. 4.一个角是钝角,它的一半是什么角? [答案] 锐角. P139习题4.3 复习巩固 1.如果把钟表的时针在任一时刻所在的位置作为起始位置,那么时针旋转出一个平角及一个周角,至少各需要多长时间? [答案] 6小时,12小时. 2.凭你的感觉画出30°,45°,90°,120°,135°的角,再用量角器量一量,你画的准确度如何? [答案] 略. 3.计算: (1)48°39′+67°31′; (2)21°17′×5. [答案] (1)116°10′;(2)106°25′. 15 4.如果∠1=∠2,∠2=∠3,则∠1________∠3; 如果∠1>∠2,∠2>∠3,则∠1________∠3. [答案] = > 5.如图,BD和CE分别是∠ABC和∠ACB的平分线,且∠DBC=∠ECB=31°,求∠ABC和∠ACB的度数,它们相等吗? [答案] ∠ABC=2∠DBC=2×31°=62°,∠ACB=2∠ECB=2×31°=62°.所以∠ABC=∠ACB. 6.按图填空: (1)∠AOB+∠BOC=________; (2)∠AOC+∠COD=________; (3)∠BOD-∠COD=________; (4)∠AOD-________=∠AOB. [答案] (1)∠AOC;(2)∠AOD;(3)∠BOC;(4)∠BOD. 7.如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进入围墙,如何测量? [答案] 延长AO或BO,先量出∠AOB的补角的度数,再计算出∠AOB的度数. 8.按照上北下南,左西右东的规定画出表示东南西北的十字线,然后在图上画出表示下列方向的射线: (1)北偏西30°; (2)南偏东60°; (3)北偏东15°; (4)西南方向(南偏西45°). [答案] (1)如图所示,射线OA表示北偏西30°; (2)如图所示,射线OB表示南偏东60°; 15 (3)如图所示,射线OC表示北偏东15°; (4)如图所示,射线OD表示西南方向. 综合运用 9.如图,OB是∠AOC的平分线,OD是∠COE的平分线. (1)如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度? (2)如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度? [答案] (1)∠BOD=70°;(2)∠AOB=40°. 10.如图,一个齿轮有15个齿,每相邻两齿中心线间的夹角都相等,这个夹角是多少度?如果是22个齿的齿轮,这个夹角又是多少度(精确到分)? [答案] 360°÷15=24°;360°÷22≈16°22′. 答:齿轮有15个齿时,相邻两齿中心线间的夹角为24°;有22个齿时,其夹角约为16°22′. 11.如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等? [答案] 在(1)中∠α与∠β互余;在(2)(3)中∠α与∠β相等;在(4)中∠α与∠β互补. 15 12.如图,A地和B地都是海上观测站,从A地发现它的北偏东60°方向有一艘船,同时,从B地发现这艘船在它北偏东30°方向.试在图中确定这艘船的位置. [答案] 如图所示,图中O点即为这艘船的位置. 13.(1)互余且相等的两个角,各是多少度? (2)一个锐角的补角比这个角的余角大多少度? [答案] (1)都是45°;(2)90°. 拓广探索 14.画几个不同的四边形,使每个四边形中都有30°,90°,105°的角,量一量这些四边形中另一个角的度数,你能发现什么规律? [答案] 图略,每一个四边形的另一个角都等于135°. 规律:四边形的四个内角的和为360°. 15.(1)图(1)中,射线AD,BE,CF构成∠1,∠2,∠3,量出∠1,∠2,∠3,并计算∠1+∠2+∠3.画出几个类似的图,计算相应的三个角的和,你有什么发现? (2)类似地,量出图(2)中∠1,∠2,∠3,∠4,计算∠1+∠2+∠3+∠4.再换几个类似的图试试,你有什么发现? 综合(1)(2)的发现,你还能进一步得到什么猜想? [答案] (1)∠1+∠2+∠3=360°.发现:无论是怎样的三角形,与每个内角相邻的三个外角的和都为360°. (2)∠1+∠2+∠3+∠4=360°,发现:无论是怎样的四边形,与每个内角相邻的四个外角的和都为360°. 综合(1)(2)发现,多边形的外角和都为360° [当堂检测] 1. 下列说法:(1)互余的两个角都是锐角;(2)若两角都是锐角,则这两角互余;(3)∠A+∠B+∠C=90°,则∠A、∠B、∠C互余;(4)同一个锐角的补角一定比它的余角大90°; (5)钝角只有余角、没有补角.其中正确的有( ) A.一个 B. 两个 C. 三个 D. 四个 2. 小明站在小颖的北偏东40°,则小颖在小明的( ) 15 A.东偏北40° B.东偏北50° C.南偏西50° D.南偏西40° 3. 如果∠α=39°31°,∠α的余角∠β =_____,∠α的补角 ∠γ=_____. 4. 如图所示,,且∠AOC=∠BOD,则∠AOC的余角是______________. 5. 一个角的余角比它的补角的 少40°,求这个角的度数. 参考答案: 1. B 2. D 3. 50°29′ 129°31′ 4. ∠BOC或∠AOD 5. 40° [能力培优] 专题一 角的个数与表示 1. 下列说法中正确的个数是( ) ①由两条射线组成的图形叫做角,②角的大小与边的长短无关,只与两条边张开的角度有关,③角的两边是两条射线,④把一个角放到一个放大10倍的放大镜下观看,角度数也扩大10倍. A.1个 B.2个 C.3个 D.4个 2.下图,在已知角内画射线,画1条射线,图中共有 3 个角;画2条射线,图中共有 6 个角;画3条射线,图中共有 10 个角,求画n条射线所得的角的个数. 专题二 钟面上的角度问题 3. 4点10分,时针与分针所夹的小于平角的角为( ) A.55° B.65° C.70° D.以上结论都不对 4.如图,在地面上有一个钟,钟面的12个粗线段刻度是整点时时针(短针)所指的位置,根据图中时针与分针(长针)所指的位置,该钟面所显示的时刻是 9 时 12 15 分. 5.周末莉莉跟妈妈去乡下的外婆家,8点多临出门她看到墙壁上钟表的时针与分针正好是重 合的,下午2点多她和妈妈回家后,一进门看见钟表的时针与分针方向相反,正好成一条 直线,问莉莉是几点钟去姥姥家?几点钟回到家?共用了多少时间? 专题三 角的折叠与拼接 6. 一副三角板不能拼出的角的度数是(拼接要求:既不重叠又不留空隙)( ) A.75° B.105° C.120° D.125° 7.一副三角板按如图所示方式重叠,若图中∠DCE=35025′则∠ACB=_________. 8.如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使DE和C′E重合,折痕是GE,你得到的∠GEF是直角吗?为什么? 专题四 角的和、差、倍、分 9.已知α、β是两个钝角,计算的值,甲、乙、丙、丁四位同学算出了四种不 同的答案分别为24°、48°、76°、86°,其中只有一个答案是正确的,则正确的答案是( ). 15 A.86° B.76° C.48° D.24° 10.计算: 11.已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=60°,∠BOC=20°, 求∠AOC的度数. 12. 已知∠AOB=∠BOC,∠COD=∠AOD=3∠AOB,求∠AOB和∠COD的度数. 13. 已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC. (1)如图①,若∠AOC=30°,求∠DOE的度数; (2)在如图①中,若∠AOC=,直接写出∠DOE的度数(用含的代数式表示); (3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置. ①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由; ②在∠AOC的内部有一条射线OF,满足:∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF 与 ∠DOE的度数之间的关系,说明理由. 15 专题五 余角、补角、方位角 14.(2012•孝感)已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( ) A.45° B.60° C.90° D.180° 15. 如图,OA的方向是北偏东15°,OB的方向是西偏北50度. (1)若∠AOC=∠AOB,则OC的方向是 北偏东70° ; (2)OD是OB的反向延长线,OD的方向是 南偏东40° ; (3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 南偏西50° ; (4)在(1)、(2)、(3)的条件下,∠COE= 160° . 16.已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数. 17.如图所示:点O是直线AB上的一点,OE平分,OD平分。 求:(1) 的度数; (2)图中互余的角有多少对?请把它们写出来.(一定要仔细哦!) 知识要点: 1.有公共端点的两条射线组成的图形叫做角. 2.1度=60分,1分=60秒.1周角=2平角=4直角=360°. 3.从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线. 4.如果两个角的和等于90°(直角),就说这两个角互为余角;如果两个角的和等于180°(平角),就说这两个角互为补角. 5.同角(等角)的余角相等;同角(等角)的补角相等. 温馨提示: 1.与角有关的注意事项: (1)角的两条边是射线,而不是线段,所以无法度量和延长. (2)角的大小与边的长短粗细无关. 15 (3)放大镜不能改变角的度数. (4)平角是一个角,它有角的内部,而直线是一条线,故不能说“平角是一条直线”.同理周角是一个角,而不是一条射线,故不能说“周角是一条射线”. 2.与角的和、差、倍、分有关的注意事项. (1)度分秒加法:度与度相加,分和分相加,秒和秒相加,计算结束后,满60进一; (2)度分秒减法:度与度相减,分和分相减,秒和秒相减,如果不够减,就向前一位借1,借1°就相当于60′,借1′就相当于60″; (3)度分秒乘法:计算结束后,满60进一;60″就相当于1′, 60′就相当于1°. (4)度分秒除法:余1°就相当于60′,余1′就相当于60″. 3.余角与补角中的注意事项: (1)互为余角、互为补角均是指两个角的关系,与第三个角无关; (2)互余、互补的两个角只与它们的和有关,而与它们的位置无关. (3)锐角的余角为锐角,锐角的补角为钝角;钝角的余角不存在,钝角的补角为锐角. (4)表示方向时我们一般书写形式为“南(北)偏东(西)×°”. 方法技巧: 1.在已知角内画n条射线所得的角的个数为:1+2+3+…+(n+1)=. 2.时钟上每格30°,时针速度0.5度/分钟,分针速度6度/分钟,这三个结论是解决时钟问题 的基本工具. 3.用一副三角板可以画0°~180°中15°的倍数的角,即15°、30°、45°、60°、75°、90°、105°、 120°、135°、150°、165°、180°.共12个角. 4.如果互补的两个角相等,那么这两个角都是直角. 5.在没有给出图形,角的位置关系不确定时,需要分类讨论. 答案: 1. B 解析:①角是有公共端点的两条射线所构成的图形,故①错误;②角的大小与边的长短 无关,只与两条边张开的角度有关,故②正确;③角的两边是两条射线,故③正确;④把一 个角放到一个放大10倍的放大镜下观看,角度数不变,故④错误. 2. 解:因为在已知角内画1条射线,图中共有3个角,即1+2=3个角;在已知角内画2条射线,图中共有6个角,即1+2+3=6个角;在已知角内画3条射线,图中共有10个角,即1+2+3+4=10个角所以在已知角内画n条射线所得的角的个数为:1+2+3+…+(n+1)=. 3. B 解析:因为4点10分时,分针从12到2转动两个格转动角度为:30°×2=60°,时针转动4×30°=125°,所以4点10分时,分针与时针的夹角是125°-60°=65°. 4. 9时12分 解析:由图可知,时针过1个大格线,走过×60=12分钟,所以,分针逆时针数12小格即为12点的位置,所以,该钟面所显示的时刻是9时12分. 5. 解:设8点x分时针与分针重合,则:6x-0.5x=180+60,解得:x=. 15 所以约8点43分时莉莉出门去姥姥家. 设2点y分时,时针与分针方向相反.则:6x-0.5x=180+60,解得:y=. 所以约2点43分时莉莉回家.所以共用了6个小时. 6. D 解:一副三角板的度数分别为:30°、60°、45°、45°、90°,因此可以拼出75°、105°和120°,不能拼出125°的角. 7. 144°35′解析:因为∠ACD=∠BCE=90°,故∠ACE=∠ACD-∠DCE=90°- 35025′=54035′. 所以∠ACB=∠ACE+∠BCE=90°+54035′=144°35′. 8. 解析:∠GEF是直角.理由如下: 由折纸实验,知∠3=∠1,∠4=∠2,而∠1+∠2+∠3+∠4=1800, 所以∠1+∠2=900,所以∠GEF是直角. 9. C 解析: 因为α、β是两个钝角,所以90°<α<180°, 90°<α<180°. 所以180°<α+β<360°,所以30°<<60°.所以C选项符合要求. 10. (4)176°52′÷3=58°+172′÷3=58°+57′+60〞÷3=58°57′20〞. 11. 解析 :若OC在∠AOB的内部,如图1,则∠AOC=∠AOB-∠BOC=60°-20°=40°;若 15 OC在∠AOB的外部,如图2,则∠AOC=∠AOB+∠BOC=60°+20°=80°.所以∠AOC的度数为40°或80°. 图1 图2 12. 解析:设∠AOB=x°,所以∠COD=∠AOD=3∠AOB=3x°. 因为∠AOB=∠BOC,所以∠BOC=2x°.因为∠BOC+∠COD+∠AOD+∠AOB=360°, 所以3x+3x+2x+x=360. 解得x=40.所以∠AOB=40°,∠COD=120°. 13. 解析:(1)因为∠AOC=30°,所以∠BOC=180°-30°=150°. 因为OE平分∠BOC,所以∠EOC=∠EOB=150°÷2=75°. 因为∠COD是直角,所以∠DOE=∠COD-∠EOC=90°-75°=15°. (2)α. (3)①∠DOE =∠AOC . 设∠DOE=x,则∠COE=90°-x,∠AOC=180-2∠COE=180-2(90-x)=2x. 所以∠DOE =∠AOC. ②4∠DOE -5∠AOF=180°,设∠DOE=x,∠AOF=y.则∠AOC=2x,∠BOE=90-x. 因为∠AOC-4∠AOF=2∠BOE+∠AOF,所以2x-4y=2(90-x)+y,所以4x-5y=180. 所以4∠DOE -5∠AOF=180°. 14. C 解析:由题意得,∠α+∠β=180°,∠α+∠γ=90°,两式相减可得:∠β-∠γ=90°.故选C. 15. 解:(1)∠AOC=∠AOB=90°-50°+15°=55°,OC的方向是北偏东15°+55°=70°; (2)OD是OB的反向延长线,OD的方向是南偏东40°; (3)OE是∠BOD的平分线,∠BOE=90°;OE的方向是南偏西50°; (4)∠COE=90°+50°+20°=160°. 16. 解:设这个角的度数是x,则(180°-x)-3(90°-x)=10°,解得x=50°.答:这个角的度数为50°. 17.解析:(1)=90°. 15 因为O是直线AB上的一点,所以 , 因为 OE平分,所以 因为 OD平分,所以 , 所以 ,即. (2)图中互余的角有4对. 例谈角在生活中的应用 学过有关角的基本知识后,能用来解决许多现实生活中所遇到的问题.下面举例谈谈角在生活中的应用. O A B 一、钟表问题. 例1 如图,是一块手表,下午2点针的时针、分针位置如图 所示,试求分针OA与时针OB所成的角的度数. 析解 若把钟表看成一个周角,其中共有12个大格, 所以每大格度数为,又由图可知包含了其中的2 份,所以. 二、台球问题 图 1 2 3 例2 如图,∠1=∠2,若∠3=,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时必须保证∠1为( ) A. B. C. D. 析解:∵∠3=,∴∠2=,∵∠1=∠2,∴∠1=.故选C. 三、折纸问题 例3 如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使DE和CE重合,折痕是GE,请探索下列问题: (1)∠FEC和∠GEC互为余角吗?为什么? (2)∠GEF是直角吗?为什么? (3)在上述折纸图形中,还有哪些互为余角?还有哪些互为补角? 解析:(1)由折纸实验,知∠3=∠1,∠4=∠2,而∠1+∠2+∠3+∠4=1800 所以∠1+∠2=900,即∠FEC+∠GEC=900,故∠FEC和∠GEC互为余角. (2)因为∠GEF=∠1+∠2=900,,所以∠GEF是直角. (3)∠3和∠4,∠1和∠EFG互为余角,∠AGF和∠DGF、∠CEC和∠DEC互为补角等 四、方位角问题 15 学校 邮局 例3 如图,在一张某地区的地图上,原标有学校、邮局、电影院三地,由于污损, 电影院的具体位置已看不清,根据记忆,电影院位置在学校的北偏东的方向,在邮局的西北方向.根据上述信息,你能在图上确定电影院的位置吗?如能,请画图说明. 解析 根据题意,电影院位置在学校的北偏东的方向上,作图时,应以学校所在地为测点,往往在此处画上“十字型”,以正北方向的射线为始边,顺时针旋转,电影院就在所得的射线上;同理,在邮局的西北方向可作出另一条射线,这两条射线的交点,即为电影院所在的位置.如图,分别从学校画北偏东的射线和从邮局画西北方向的射线,两射线的交点就是电影院的位置. 学校 邮局 电影院 15查看更多